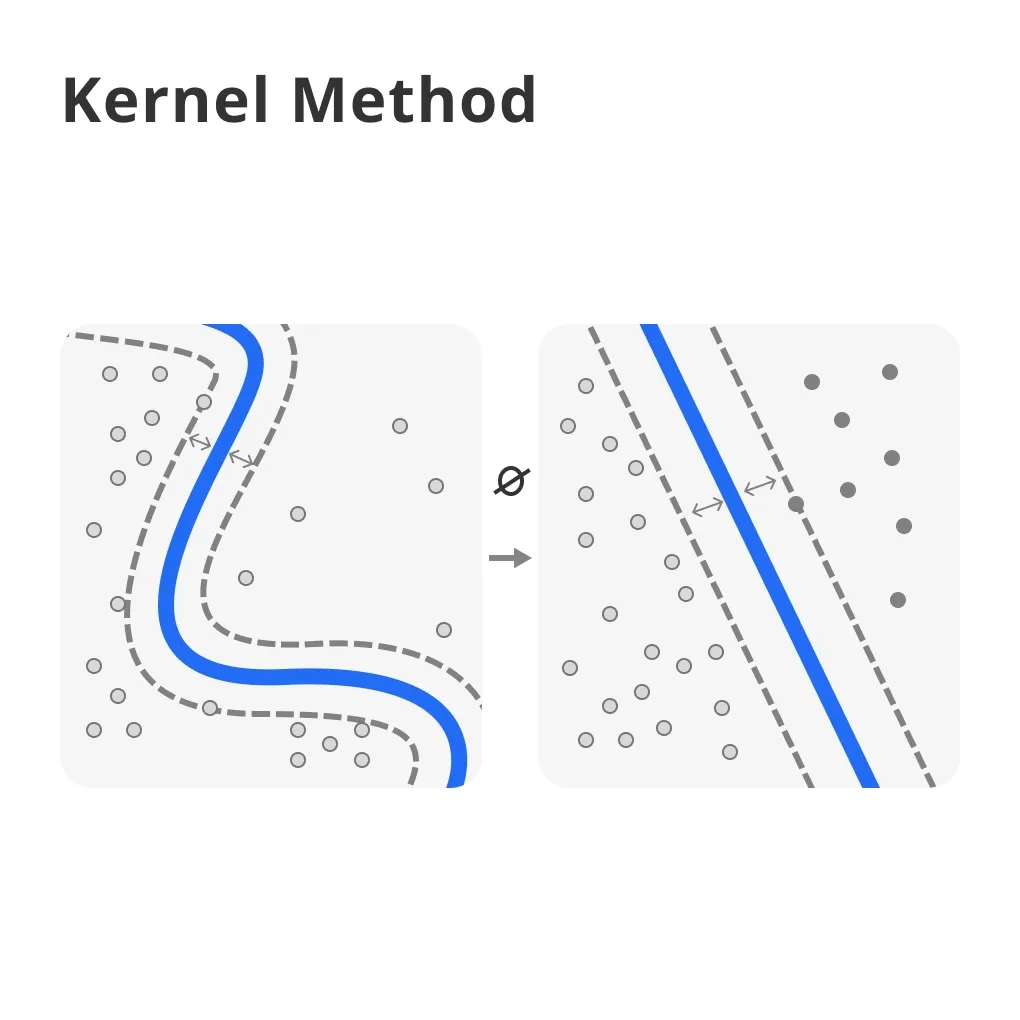
What are Kernel Methods?
At their core, kernel methods are techniques used to tackle linear and non-linear problems by applying transformations to the data, which allow linear methods to be applied to non-linear problems.
This is done without ever having to explicitly compute the coordinates in the higher-dimensional space, thanks to the magic of kernel functions.
Definition
A kernel function, in essence, calculates the dot product between two points in a feature space. This dot product corresponds to the similarity between the two points—the more similar the points are, the larger the dot product.
Key Components
The key components of kernel methods include the kernel function itself, the input space where our initial data points live, and the feature space, which is the higher-dimensional space where our data points are mapped to by the kernel function.
Common Kernel Functions
There are several common kernel functions, including linear, polynomial, radial basis function (RBF), and sigmoid kernels. Each has its own set of applications and suitability depending on the problem at hand.
Applications
Kernel methods are widely used in various machine learning tasks such as classification, regression, and clustering.
Specific algorithms that utilize kernel methods include Support Vector Machines (SVM), Principal Component Analysis (PCA), and Kernel Ridge Regression.
Advantages
Kernel methods allow complex relationships in data to be captured. They are also versatile in handling any type of data—be it vectors, text, images, or graphs.
Why Use Kernel Methods?
Kernel methods are celebrated across various domains of data science for their versatility and efficacy. But why exactly should one consider using them?
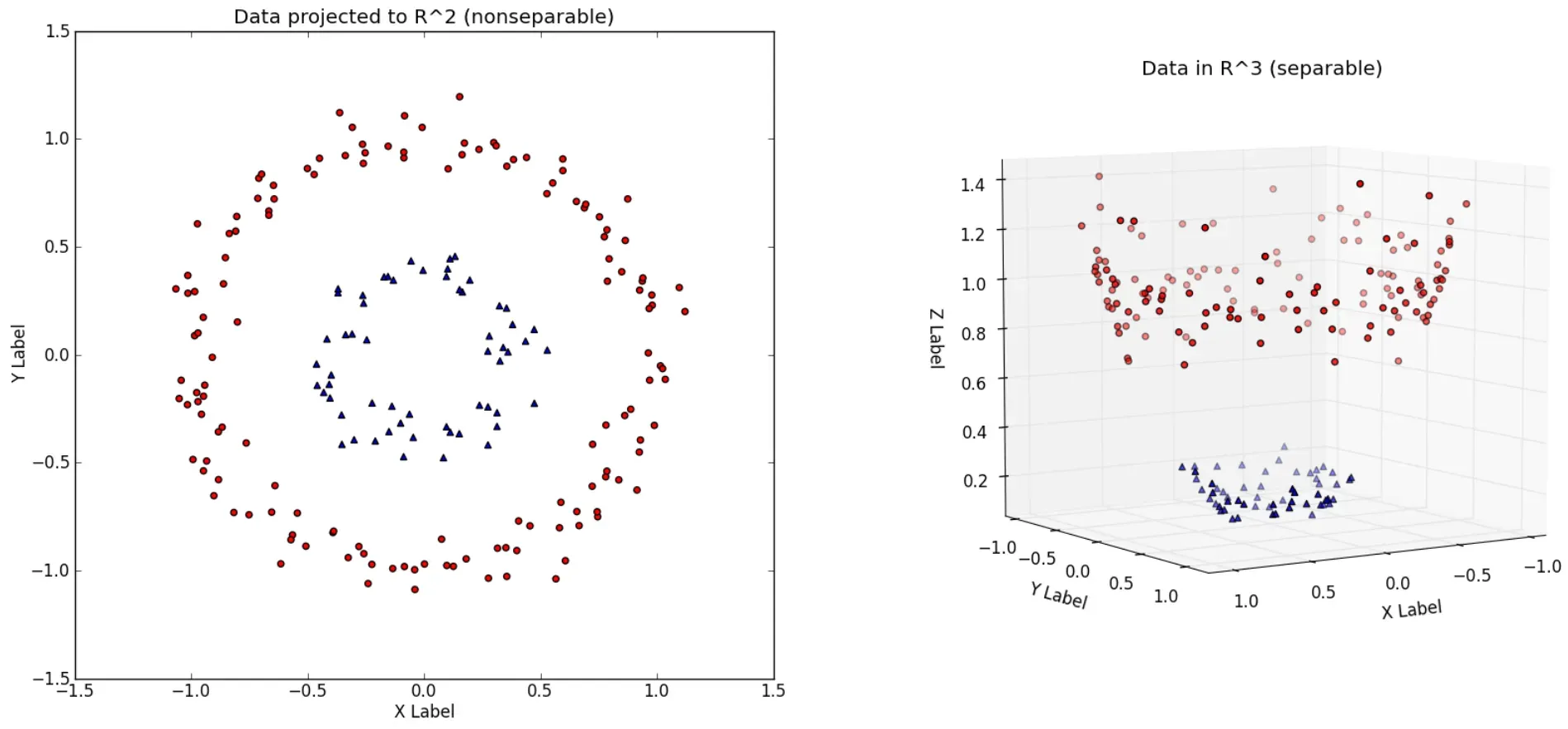
Handling Non-linear Data
One of the most compelling reasons to use kernel methods is their ability to handle non-linear relationships in data effortlessly.
High Dimensional Feature Spaces
Kernel methods facilitate working in high dimensional spaces without the need for explicit mapping, making it computationally efficient to capture complex patterns.
Flexibility
The choice of the kernel function offers flexibility, allowing the kernel method to be tailored to the specific needs of the data or problem.
Theoretical Foundations
Kernel methods are underpinned by robust theoretical foundations, providing clear guidelines for their application and ensuring predictable outcomes.
Performance
Time and again, kernel methods have been shown to perform exceptionally well on a wide range of machine-learning tasks.
How Do Kernel Methods Work?
Understanding the operation of kernel methods helps in appreciating their elegance and power.
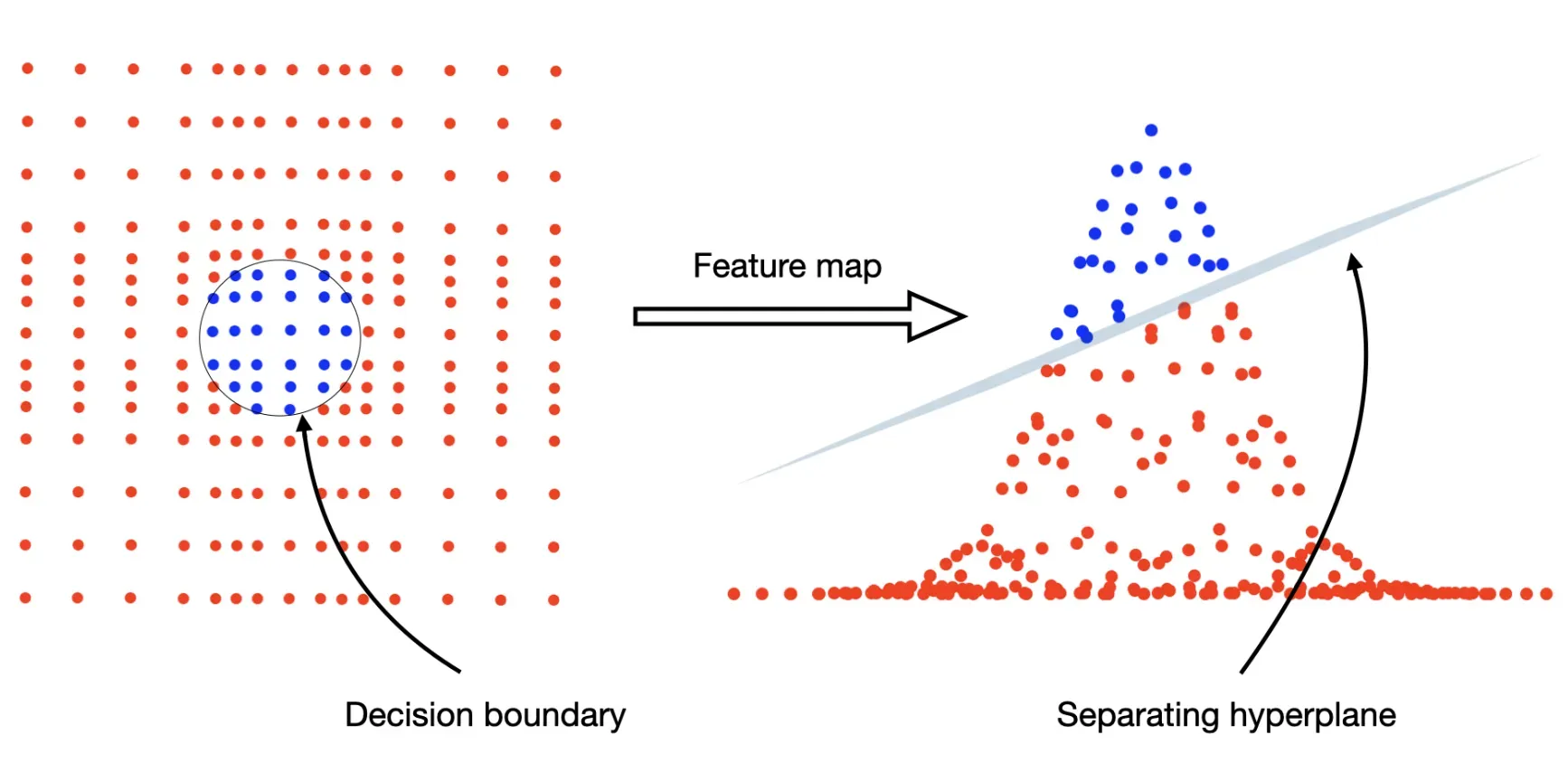
Mapping to Higher-Dimensional Space
Data is implicitly mapped to a higher-dimensional space where linear relationships and separations are easier to find.
Computing the Kernel Matrix
The kernel function computes the similarity between pairs of points in this higher-dimensional space, resulting in a kernel matrix.
Solving in Dual Space
Machine learning algorithms, instead of operating directly on the features, work on the kernel matrix to find patterns and make predictions.
The Trick: Kernel Trick
The kernel trick allows the computation of the kernel matrix without explicitly computing the coordinates in the higher-dimensional space, offering computational efficiency.
Returning to Original Space
After the machine learning task is accomplished in the higher-dimensional feature space, the results or predictions are interpreted or represented back in the original input space.
When to Use Kernel Methods?
Identifying the scenarios where kernel methods shine can guide their effective application.
Complex, Non-linear Problems
Kernel methods are particularly suited for problems where the relationship between the variables is non-linear.
High-Dimensional Data
For datasets with a large number of features, kernel methods can efficiently capture interactions without the curse of dimensionality.
Text and Image Data
Their ability to handle various types of data makes kernel methods ideal for text and image analysis tasks, where data is inherently high-dimensional and complex.
Small to Medium-sized Datasets
While kernel methods are powerful, they are best suited for datasets of small to medium size due to computational considerations.
Tasks Requiring Flexibility
The ability to choose or design a kernel function based on the problem at hand makes kernel methods highly adaptable to a wide range of tasks.
Who Benefits from Kernel Methods?
Kernel methods are not confined to a niche; a broad spectrum of fields can leverage their power.
Data Scientists
For data scientists wrestling with complex, high-dimensional datasets or non-linear relationships, kernel methods provide a robust analytical tool.
Researchers in Machine Learning
Researchers exploring theoretical or applied aspects of machine learning find kernel methods to be a fertile ground for innovation and exploration.
Industry Professionals
Professionals in industries ranging from finance to healthcare utilize kernel methods to extract insights from data and inform decision-making processes.
Programmers in AI and ML
Developers and programmers in artificial intelligence and machine learning implement kernel methods to enhance the capabilities of AI systems.
Academics
In academia, kernel methods are both a subject of research and a tool for dissecting complex datasets in various fields of study.
Best Practices for Kernel Methods
Implementing kernel methods effectively calls for adherence to certain best practices.
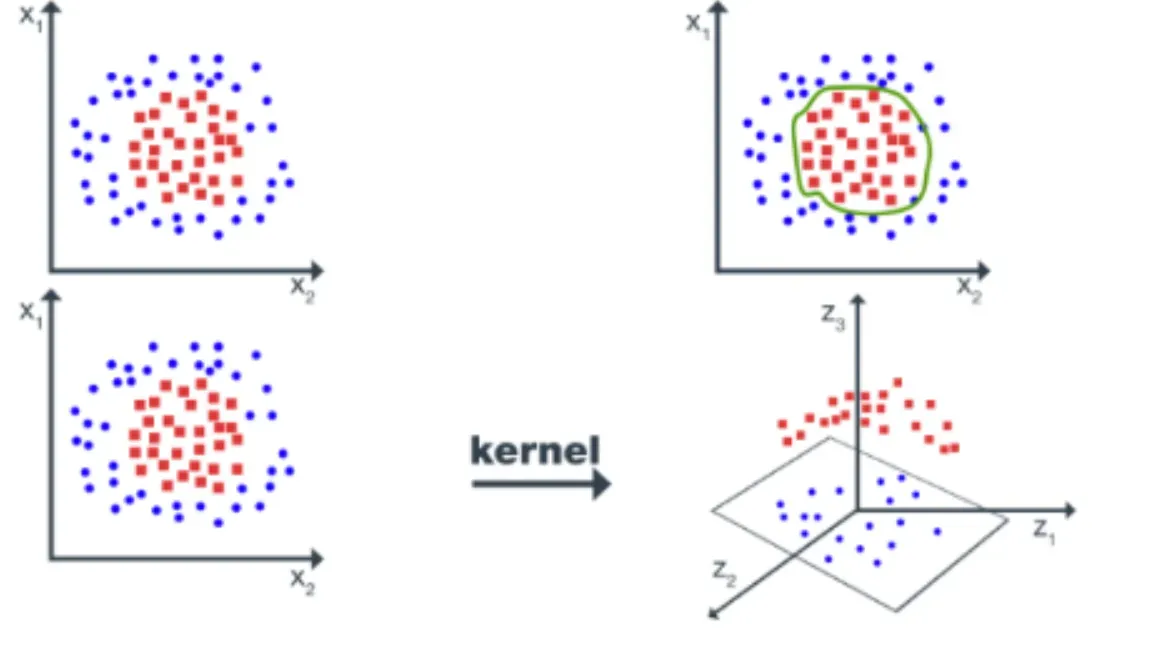
Choosing the Right Kernel
Selecting or designing the appropriate kernel function for the task and data at hand is vital for the success of kernel methods.
Regularization
To prevent overfitting, especially in high-dimensional spaces, it's crucial to employ regularization techniques.
Scalability Considerations
For larger datasets, considering the computational complexity and exploring scalable kernel methods or approximations is important.
Cross-validation
Employing cross-validation techniques to fine-tune the parameters of the kernel method ensures robust performance across different datasets.
Continuous Monitoring
Monitoring the performance of kernel method-based models and being ready to update them as more data becomes available or conditions change ensures ongoing relevance and accuracy.
Challenges in Kernel Methods
Despite their potent capabilities, kernel methods come with their own set of challenges.
Computational Cost
The computational complexity of kernel methods, especially with large datasets, is a significant hurdle.
Choosing Kernel and Parameters
The process of selecting the most appropriate kernel and fine-tuning its parameters can be non-trivial and time-consuming.
Risk of Overfitting
In high-dimensional feature spaces, there's an increased risk of overfitting, necessitating careful regularization.
Interpretability
The transformations that kernel methods apply can make the resulting models less interpretable than their linear counterparts.
Data Dependence
The performance of kernel methods can be highly dependent on the data quality and the appropriateness of the chosen kernel function.
Trends in Kernel Methods
The landscape of kernel methods is continually evolving, driven by both new theoretical insights and practical applications.
Deep Kernel Learning
Combining kernel methods with deep learning models opens new frontiers in both interpretability and performance.
Large-scale Kernel Methods
Advancements in algorithms and computing infrastructure are making kernel methods more viable for large-scale applications.
Kernel Methods in Unsupervised Learning
Exploration of kernel methods in unsupervised learning contexts, such as clustering and dimensionality reduction, is expanding their applicability.
Integration with Other Machine Learning Paradigms
Kernel methods are being integrated with other machine learning paradigms, offering hybrid approaches that leverage the strengths of each.
Automated Kernel Selection
Research into automated selection and tuning of kernel functions using machine learning approaches themselves is making kernel methods more accessible and effective.
TL;DR
Kernel methods stand as a testament to the beauty and power of mathematical abstraction and its applicability to solving real-world problems. From enabling machines to understand complex, non-linear relationships in data to paving the way for innovative approaches in AI, kernel methods continue to be a foundational pillar in the field of machine learning.
Whether you're a seasoned data scientist, an AI programmer, or a machine learning enthusiast, mastering kernel methods opens up a world of possibilities for data analysis, predictive modeling, and beyond.
Frequently Asked Questions (FAQs)
What's the Advantage of Using Kernel Methods in Non-linear Problems?
Kernel methods allow non-linear problems to be transformed and solved as linear ones in higher-dimensional feature spaces, without explicitly computing dimensions.
Can Kernel Methods Be Used in Clustering?
Yes, kernel methods can be used in clustering algorithms, such as Kernel K-means, to find clusters in non-linearly separable data.
How Does the Choice of Kernel Affect Model Performance?
The choice of kernel function has a significant impact, as it determines the feature space and how effectively data can be classified or clustered.
Are Kernel Methods Specific to Support Vector Machines?
While commonly associated with SVMs, kernel methods are also used in other algorithms, such as PCA and ridge regression, for handling non-linear data.
How Do Kernel Methods Handle High-Dimensional Data?
Kernel methods can efficiently deal with high-dimensional data by projecting it into a suitable feature space for relevant analysis or classification.