Introduction
Ridge regression is a cheat code for statistics. Surprised? You should be. Traditional linear regression has its flaws, especially when dealing with multicollinearity.Imagine a world where predictive models are more accurate and stable. This is not a dream but a reality with ridge regression. It penalizes the size of coefficients, which helps in reducing overfitting.
In this guide, we’ll explore how ridge regression works, why it’s a game changer, and how you can apply it in your own data analysis.
What is Ridge Regression
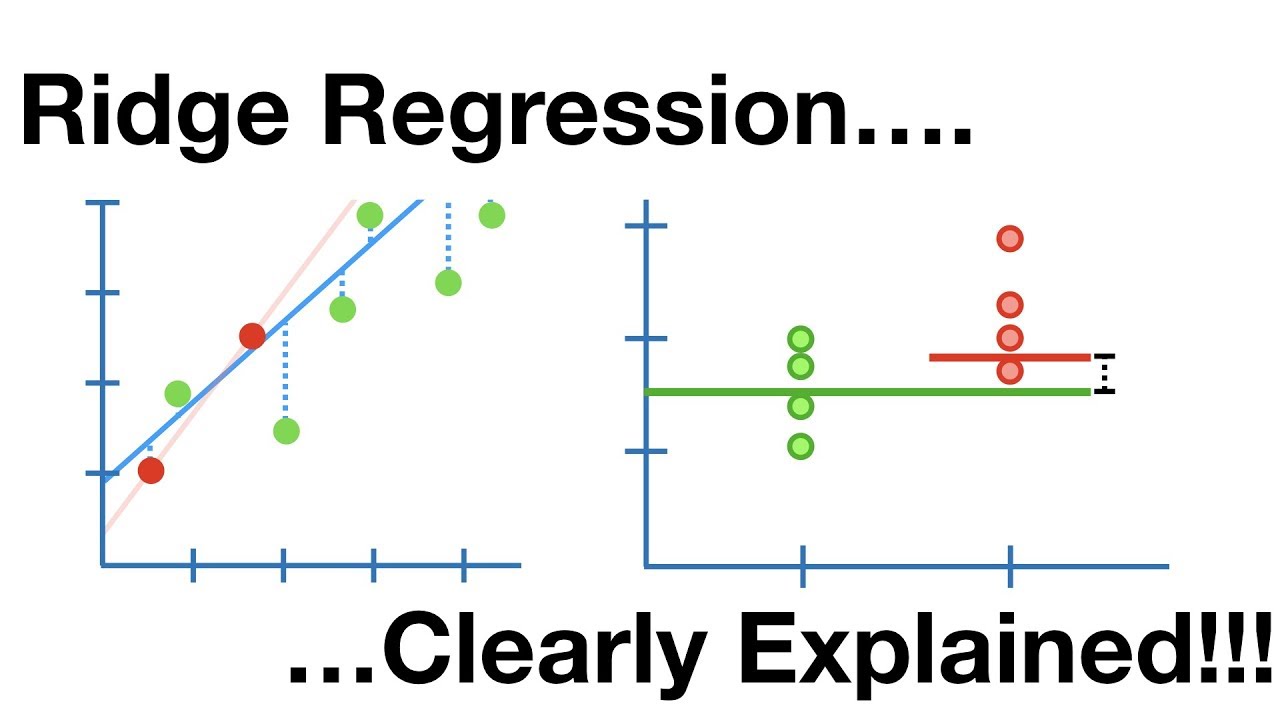
Ridge Regression is a type of linear regression that includes a regularization parameter. It adds a penalty to the size of the coefficients to reduce overfitting. This penalty term is the sum of the squares of the coefficients multiplied by a constant, known as the regularization parameter. The main goal is to find the best balance between fitting the data well and keeping the model simple.
Ridge Regression is a powerful tool for dealing with multicollinearity in linear regression models. By adding a degree of bias to the regression estimates, it helps to reduce standard errors. This method is particularly useful when dealing with data that has many predictors, and it aims to improve the model's predictive accuracy.
How Ridge Regression Works
The ridge regression works in the following way:
- Regularization Parameter: The regularization parameter (lambda) controls the strength of the penalty. A higher value of lambda results in greater shrinkage of the coefficients. For example, when predicting house prices, Ridge Regression might assign lower weights to less important features, like the number of trees in the yard, while giving more weight to significant features like the square footage.
- Bias-Variance Trade-off: By introducing bias through the penalty, Ridge Regression reduces variance. In real-world applications, such as predicting sales based on multiple marketing strategies, this trade-off helps in creating a model that generalizes better to new data.
- Multicollinearity Handling: Ridge Regression is particularly useful in situations where predictors are highly correlated. For instance, in medical data where various health metrics might be interrelated, Ridge Regression helps in maintaining a robust model by reducing the impact of multicollinearity.
Mathematics Behind Ridge Regression Formula
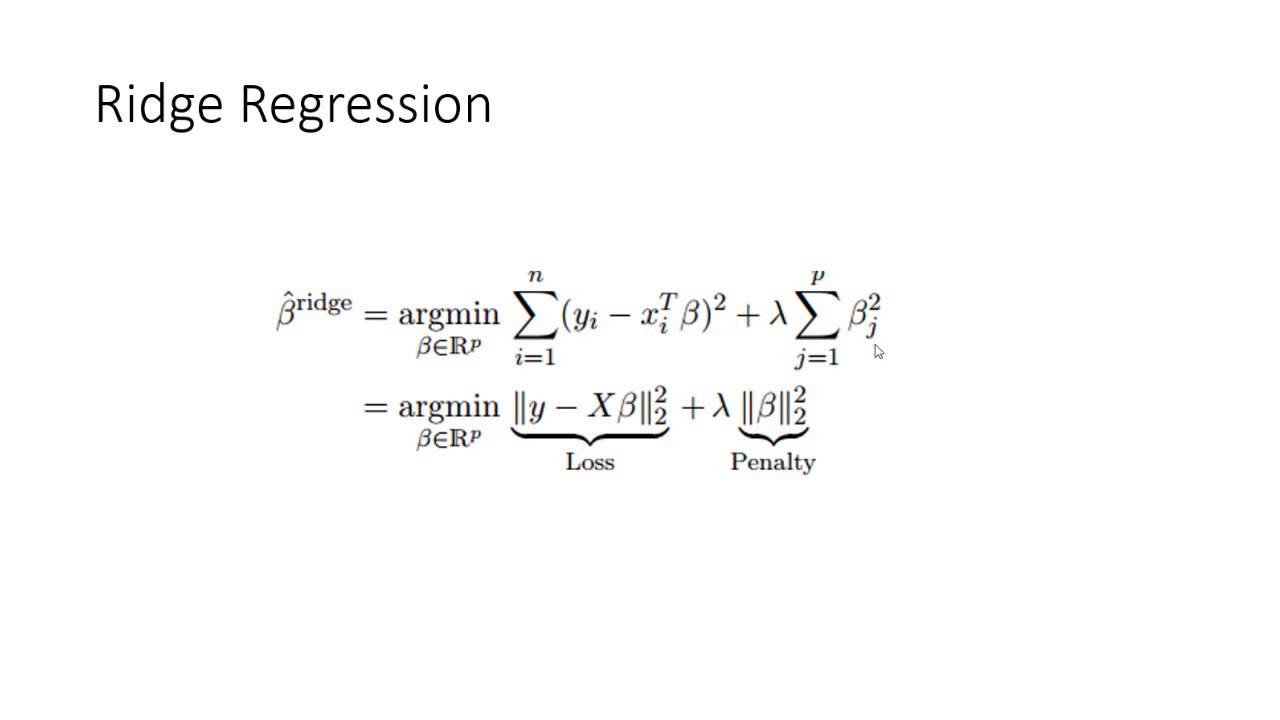
Understanding the mathematical foundation of Ridge Regression helps us appreciate its role in improving model accuracy by addressing multicollinearity and preventing overfitting.
Ridge Regression Formula
The Ridge Regression formula modifies the standard linear regression equation by adding a penalty term. The Ridge Regression formula is:
min ∑i=1n(yi−β0−∑j=1pβjxij)2+λ∑j=1pβj2\textbf{min} \, \sum_{i=1}^{n} (y_i - \beta_0 - \sum_{j=1}^{p} \beta_j x_{ij})^2 + \lambda \sum_{j=1}^{p} \beta_j^2min∑i=1n(yi−β0−∑j=1pβjxij)2+λ∑j=1pβj2
In this Ridge Regression formula:
- yiy_iyi represents the actual output.
- β0\beta_0β0 is the intercept.
- βj\beta_jβj denotes the coefficients for each predictor xijx_{ij}xij.
- λ\lambdaλ is the regularization parameter.
Explanation of the Regularization Term
The regularization term, λ∑j=1pβj2\lambda \sum_{j=1}^{p} \beta_j^2λ∑j=1pβj2, is crucial in Ridge Regression. It controls the magnitude of the coefficients. By adding this term, the algorithm penalizes larger coefficients, thus shrinking them towards zero. This helps in reducing the model complexity.
Advantages of Ridge Regression
Exploring the advantages of Ridge Regression helps us understand why it is a preferred method for many regression problems. Its unique ability to handle multicollinearity and enhance model performance makes it a valuable tool for data scientists and analysts.
Handling Multicollinearity
Ridge Regression effectively addresses multicollinearity, which occurs when predictors are highly correlated. In such cases, traditional linear regression struggles, producing unreliable estimates. Ridge Regression mitigates this issue by adding a penalty to the coefficients, resulting in more stable and interpretable estimates. For example, in financial modeling, where variables like interest rates and economic indicators are often correlated, Ridge Regression provides more reliable predictions.
Suggested Reading: Large Language Models
Improving Model Performance
By shrinking the coefficients, Ridge Regression enhances model performance, particularly in datasets with many predictors. It prevents the model from fitting the noise, leading to better generalization on unseen data. This makes it ideal for applications like predicting consumer behavior, where numerous factors influence purchasing decisions.
Suggested Reading: Dynamic Models
Preventing Overfitting
Ridge Regression is instrumental in preventing overfitting, a common problem where the model performs well on training data but poorly on new data. The regularization term ensures the model remains simple, improving its ability to generalize. In healthcare data analysis, for instance, Ridge Regression helps in building robust models that predict patient outcomes reliably, even with complex and varied datasets.
What Is The Difference Between Lasso vs Ridge regression?

Lasso and Ridge regression are both regularization techniques used to prevent overfitting. But both Lasso and Ridge regression differ in how they handle features and penalties. It makes Lasso and Ridge regression suitable for different types of data and problems. So continue reading to know more about the Lasso vs Ridge regression.
Lasso Regression
In the conflict of Lasso vs Ridge regression, here is the information about the Lasso regression.
- Feature Selection: Lasso (Least Absolute Shrinkage and Selection Operator) can shrink some coefficients to zero, effectively selecting a subset of features.
- Sparsity: Ideal for models needing sparse solutions, as it can handle situations where only a few predictors are significant.
- Overfitting: Reduces overfitting by imposing an L1 penalty, which constrains the sum of absolute values of coefficients.
- Interpretability: Easier to interpret due to fewer non-zero coefficients.
- Performance: Can perform poorly if features are highly correlated, as it may randomly select one feature over another.
Ridge Regression
In the difference between Lasso vs Ridge regression, here is the basics of Ridge regression.
- Feature Selection: Ridge regression does not set coefficients to zero, so it includes all features in the model.
- Multicollinearity: Effective in dealing with multicollinearity by shrinking coefficients of correlated features.
- Overfitting: Reduces overfitting through an L2 penalty, which constrains the sum of squared coefficients.
- Complexity: Produces a more complex model since it retains all features.
- Performance: Tends to perform better when many features have small to moderate effect sizes.
Comparison Between Lasso vs Ridge regression
Here is the final comparison between Lasso and Ridge regression:
- Penalties: Lasso uses L1 penalty (sum of absolute values), Ridge uses L2 penalty (sum of squared values).
- Feature Selection: Lasso can perform automatic feature selection, Ridge cannot.
- Model Complexity: Lasso leads to simpler models, Ridge leads to models retaining all features.
- Use Cases: Lasso is preferred when feature selection is needed; Ridge is preferred when dealing with multicollinearity.
Frequently Asked Questions (FAQs)
When should Ridge Regression be used?
Ridge Regression should be used when there is multicollinearity in the data, meaning predictor variables are highly correlated. It helps stabilize the model by adding a penalty to large coefficients, reducing variance without significantly increasing bias.
How does Ridge Regression differ from Linear Regression?
Ridge Regression differs from Linear Regression by including a regularization term (lambda) in its cost function. This term penalizes large coefficients, helping to prevent overfitting and improve the model's performance on new data.
What is the role of the lambda parameter in Ridge Regression?
The lambda parameter controls the strength of the penalty applied to the coefficients. A higher lambda value increases the penalty, leading to smaller coefficients, while a lower lambda value results in a model closer to standard linear regression.
How to choose the best lambda value in Ridge Regression?
To choose the best lambda value, use cross-validation techniques like k-fold cross-validation or grid search. These methods evaluate different lambda values on a validation set to find the one that minimizes prediction error.
What are the advantages of Ridge Regression?
Ridge Regression handles multicollinearity well, prevents overfitting, and can improve model performance by shrinking coefficients. It is especially useful when there are many predictors, and some are highly correlated.
