What is Dimensionality Reduction?
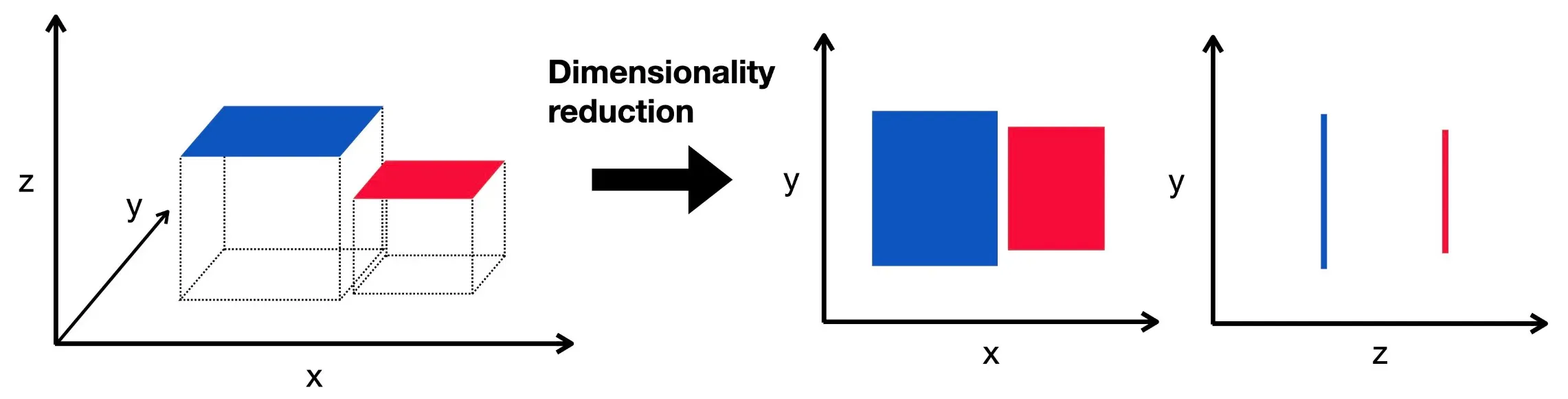
Dimensionality Reduction is a technique used in machine learning and data science to reduce the number of input variables in a dataset.
While maintaining the dataset's essential structure and integrity, it simplifies the dataset, making it easier to understand, visualize, and process.
Purpose of Dimensionality Reduction
Dimensionality reduction can help to remove redundant features, decrease computation time, reduce noise, and improve the interpretability of a dataset, thereby enhancing machine learning model performance.
Importance of Dimensionality Reduction
In the era of big data, datasets with hundreds or even thousands of features are common. However high dimensionality often leads to overfitting and poor model performance—referred to as the curse of dimensionality. Here, dimensionality reduction acts as a savior, mitigating these issues.
Types of Dimensionality Reduction
Dimensionality reduction techniques primarily fall under two categories: feature selection and feature extraction.
Feature selection techniques pick a subset of the original features, while feature extraction techniques create new composite features from the original set.
Popular Techniques in Dimensionality Reduction
Some of the most widely used dimensionality reduction techniques include Principal Component Analysis (PCA), Linear Discriminant Analysis (LDA), Generalized Discriminant Analysis (GDA), and various forms of nonlinear dimensionality reduction like t-Distributed Stochastic Neighbor Embedding (t-SNE) and Autoencoders.
Why is Dimensionality Reduction Necessary?
Now let's understand why dimensionality reduction is such an essential part of modern data science and machine learning.
Alleviating the Curse of Dimensionality
High-dimensional data often results in degraded model performance, a phenomenon known as the curse of dimensionality. Dimensionality reduction can alleviate such issues, enhancing model accuracy and speed.
Improving Model Performance
Dimensionality reduction can filter out noise and redundant features, significantly improving the performance of machine learning models.
Efficient Data Visualization
Humans can't visualize data in dimensions higher than three. By reducing high-dimensional data to two or three dimensions, we can visualize and better understand the data.
Reducing Storage Space and Processing Time
High-dimensional data requires substantial storage and computing power. By reducing the data's dimensionality, we can significantly downsize storage requirements and speed up processing time, leading to more efficient computations.
Handling Multicollinearity
Multicollinearity, a scenario where one feature can be linearly predicted from others, can harm model performance. Dimensionality reduction can be a remedy, as it creates a new set of orthogonal features.
Where is Dimensionality Reduction Applied?
Dimensionality reduction possesses wide applicability. Let's explore a few of its use cases across different domains.
Data Science
In data science, dimensionality reduction is used to make high-dimensional data more understandable and manageable. It is key to various aspects of data exploration, visualization, and preprocessing.
Machine Learning and AI
For machine learning and AI, dimensionality reduction is an essential part of preprocessing. It's used extensively in various learning tasks like regression, classification, and clustering.
Image Processing
In image processing, each pixel can be considered a feature, leading to extremely high-dimensional data. Dimensionality reduction helps simplify these datasets, aiding in tasks such as image recognition and compression.
Natural Language Processing (NLP)
In NLP, texts are often represented in high dimensions, where each word or phrase is a separate dimension.
Techniques like Latent Semantic Analysis — a type of dimensionality reduction — are used to simplify text data and discover underlying themes or topics.
Bioinformatics
High-dimensional genomic and proteomic data are prevalent in bioinformatics. Dimensionality reduction is crucial in identifying patterns in these datasets and aiding disease diagnosis and personalized medicine development.
How is Dimensionality Reduction Applied?
We have acquainted ourselves with what dimensionality reduction is and why it's necessary. Now, let's delve into how it is practically applied in various scenarios.
Checking for Redundant Features
Removing redundant or irrelevant features is the simplest type of dimensionality reduction. Using methods like correlation matrices, we can find and remove these unnecessary features.
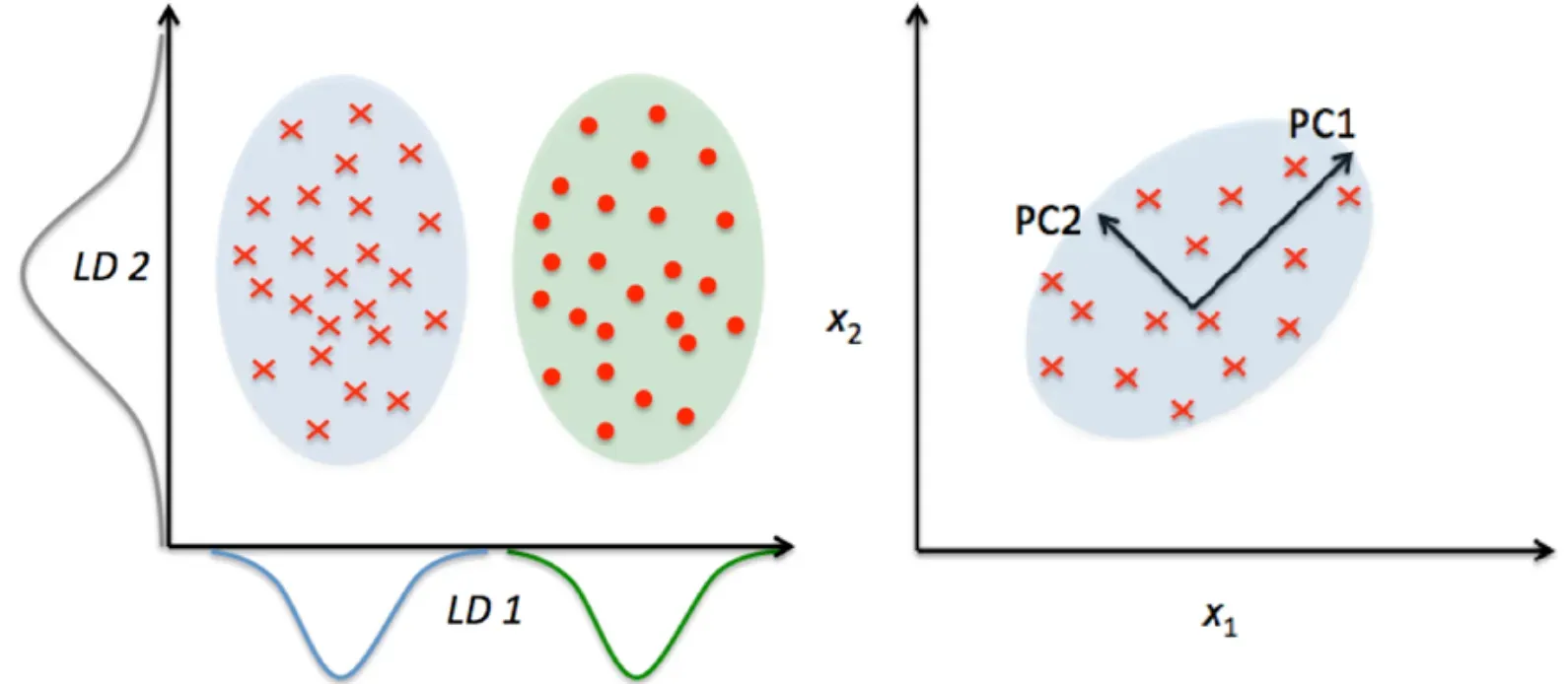
Principal Component Analysis (PCA)
PCA is a popular linear technique that projects data onto fewer dimensions. It constructs new features called principal components, which are linear combinations of original features. These principal components capture the maximum variance in the data.
Linear Discriminant Analysis (LDA)
LDA, used for classification tasks, aims to find a linear combination of features maximizing the class separability. It is a supervised method, implying it requires class labels for performing dimensionality reduction.
t-SNE and UMAP
t-SNE and UMAP are non-linear methods popular for visualizing high-dimensional data. They try to preserve the local and global structure of the data while projecting to low dimensions.
Autoencoders
Autoencoders are neural networks used for dimensionality reduction. They encode high-dimensional inputs into lower-dimensional representations, which are then decoded back.
The trained encoder part can serve as a dimensionality reduction model.
Suggested Reading:
Denoising Autoencoders: Future Trends & Examples
Best Practices in Dimensionality Reduction
It may seem that dimensionality reduction is always beneficial, but is it so? Let's deliberate on some best practices to avoid pitfalls while applying dimensionality reduction.
Impact on Model Performance
Always check the impact of dimensionality reduction on your model's performance. It may not always improve the performance and, in some cases, may even reduce the model's prediction capabilities.
Interpretability Tradeoff
While reducing dimensionality can make your data more manageable, it may come at the cost of losing interpretability.
Especially with methods like PCA, where new features are a combination of original features, understanding their implications can be challenging.
Feature Selection vs Feature Extraction
While selecting a technique, be mindful of whether you want to maintain the original features (feature selection) or create new features (feature extraction). It depends on the problem at hand and the interpretability level you desire.
Explore the Data
Before applying dimensionality reduction, explore your data. Understand the features, their correlation, and their importance, and only then decide which features to keep.
Experiment with Different Techniques
In dimensionality reduction, there is no one-size-fits-all. The most suitable technique depends on the dataset and the problem at hand. Hence, try and test different techniques and select the one that works best for your specific case.
Challenges in Dimensionality Reduction
As beneficial as it might sound, dimensionality reduction is not devoid of challenges. Let's discuss some key challenges that one might encounter.
Losing Important Information
While reducing dimensions, there's always a risk of losing useful information that might influence the model's predictive accuracy.
Technique Selection
Selection of the right technique for dimensionality reduction can pose a challenge as it largely depends on the data and the business problem at hand.
Computational Complexity
For incredibly high-dimensional datasets, certain dimensionality reduction techniques can be computationally expensive.
Data Distortion
Some dimensionality reduction techniques might project the data into a space in a way that distorts distances between points or the density distribution, thereby misleading further analysis.
Scale Sensitivity
Many dimensionality reduction techniques are sensitive to the scale of features. Hence, standardizing the features before applying dimensionality reduction is crucial to obtain reasonable results.
Trends in Dimensionality Reduction
Lastly, considering the rapid advancements in technology, it's imperative to take note of trends in dimensionality reduction.
Embeddings in Deep Learning
Word embeddings in NLP and embeddings for categorical variables in deep learning are emerging trends in dimensionality reduction.
Automated ML Pipelines
As part of the AutoML trend, dimensionality reduction is being automated with pipelines dynamically selecting the best techniques for given data.
Manifold Learning
New techniques are being developed to achieve better dimensionality reduction, especially focusing on maintaining the manifold structure of high-dimensional data.
Better Visualization Techniques
Visualizing high-dimensional data is always a challenge. Advanced visualizations like 3D and interactive plots are being used to better understand the resulting lower-dimensional data.
Integration with Big Data Tools
With the prevalence of Big Data, dimensionality reduction techniques are increasingly integrated with big data platforms to handle the growing volume and complexity of data.
Frequently Asked Questions (FAQs)
Why is Dimensionality Reduction Important in Machine Learning?
Dimensionality reduction can simplify the model, expedite learning, and reduce noise by eliminating irrelevant features, improving computational efficiency.
How can Dimensionality Reduction prevent Overfitting?
By reducing features, dimensionality reduction minimizes the complexity of the model, thereby limiting the risk of overfitting the data.
What's the difference between feature Selection and Feature Extraction?
Both are dimensionality reduction techniques. Feature selection picks a subset of original features; feature extraction creates new features by combining the original ones.
How does Principal Component Analysis (PCA) Work in dimensionality reduction?
PCA transforms a set of correlated variables into a smaller set of uncorrelated variables, called principal components, while retaining maximum variance.
Is t-distributed Stochastic Neighbor Embedding (t-SNE) a form of dimensionality reduction?
Yes, t-SNE is a technique designed for visualizing high-dimensional data by reducing it to two or three dimensions, while preserving local relationships.