What is Linear Discriminant Analysis (LDA)?
Linear Discriminant Analysis (LDA) is a powerful and commonly used tool in the field of statistics and machine learning.
It's all about classifying our data and understanding the factors that impact differing categories. Let's dive into the A-Z of LDA, so grab your snorkels because we're diving deep, no geek-speak guaranteed.
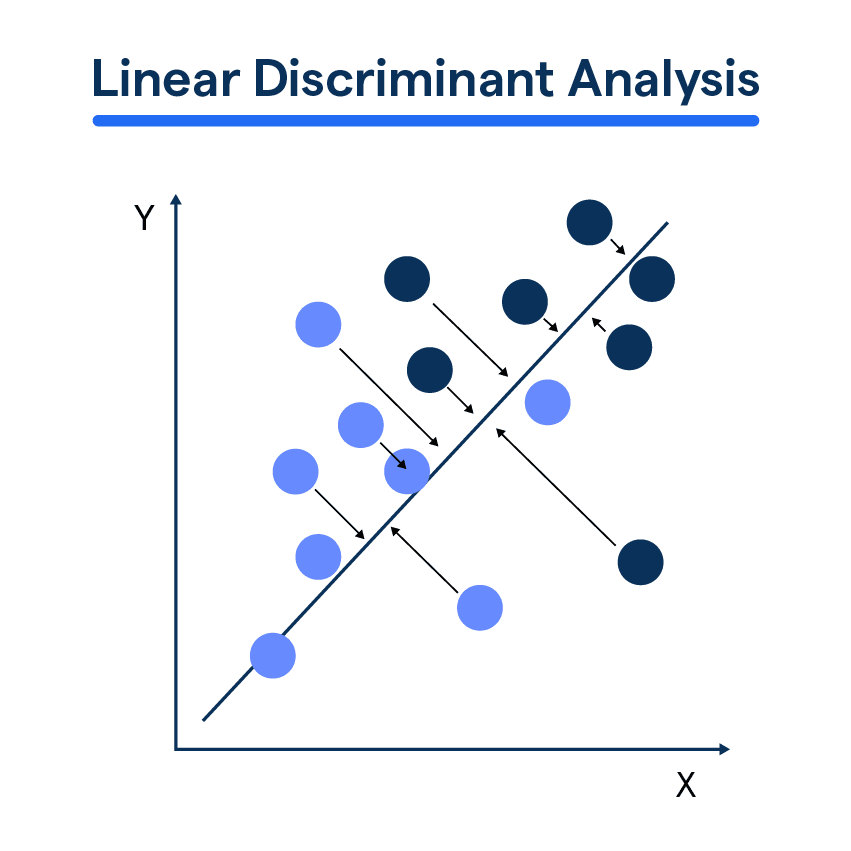
At its core, LDA is all about finding a linear combination of features that separates or characterizes two or more classes of objects or events.
Statistical Roots
LDA's origin lies in statistics where it was used as a technique for binary and multiclass classification under the assumption of normally distributed classes with identical covariance matrices.
Use in Machine Learning
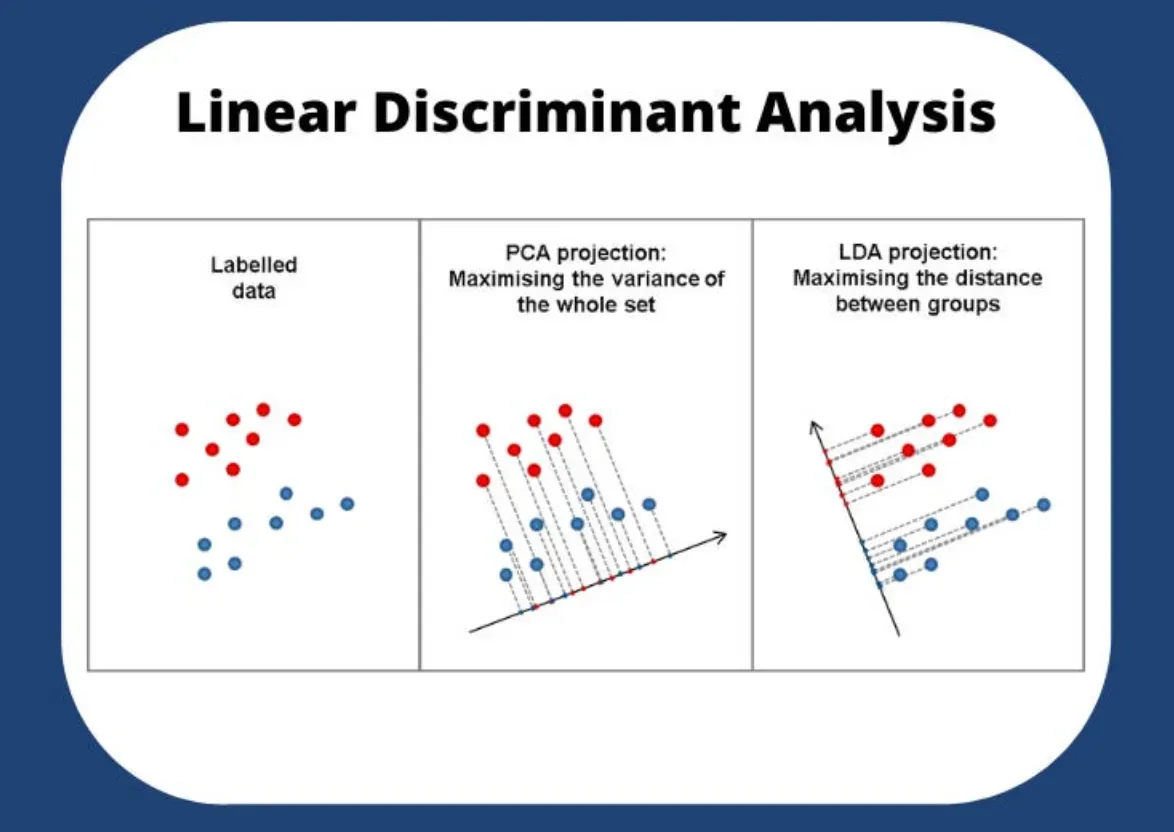
In the world of machine learning, LDA is a popular method for dimensionality reduction that compares favorably to PCA (Principal Component Analysis) when the classes are well-separated.
Predictive Analytics
LDA forms a vital part of predictive analytics, providing an effective classification mechanism when applied to categorical dependent variables.
Assumptions in Linear Discriminant Analysis
Crack open any analysis technique, and you'll find a list of assumptions. Fear not, the ones for LDA are straightforward and easy to comprehend.
Normality
LDA assumes that the variables for each class are drawn from a multivariate normal distribution. It's a fancy way of saying that the variables are more or less evenly spread around the mean.
Homoscedasticity
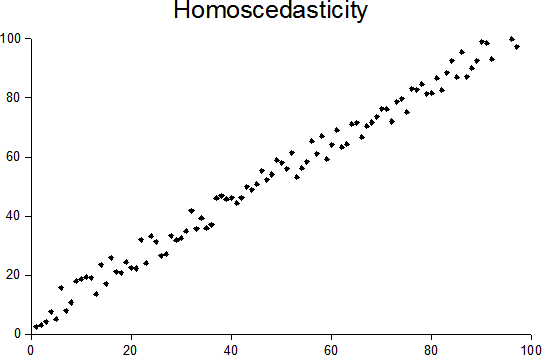
There's a couple of big words for you! Simply put, LDA assumes that the spread, or variances, of the variables among the groups are equal.
Independent Observations
LDA also assumes that any two groups are independent of each other. Essentially, one group doesn't influence the other.
Linearity
Finally, LDA assumes a linear relationship between independent (input) variables and the dependent (output) category.
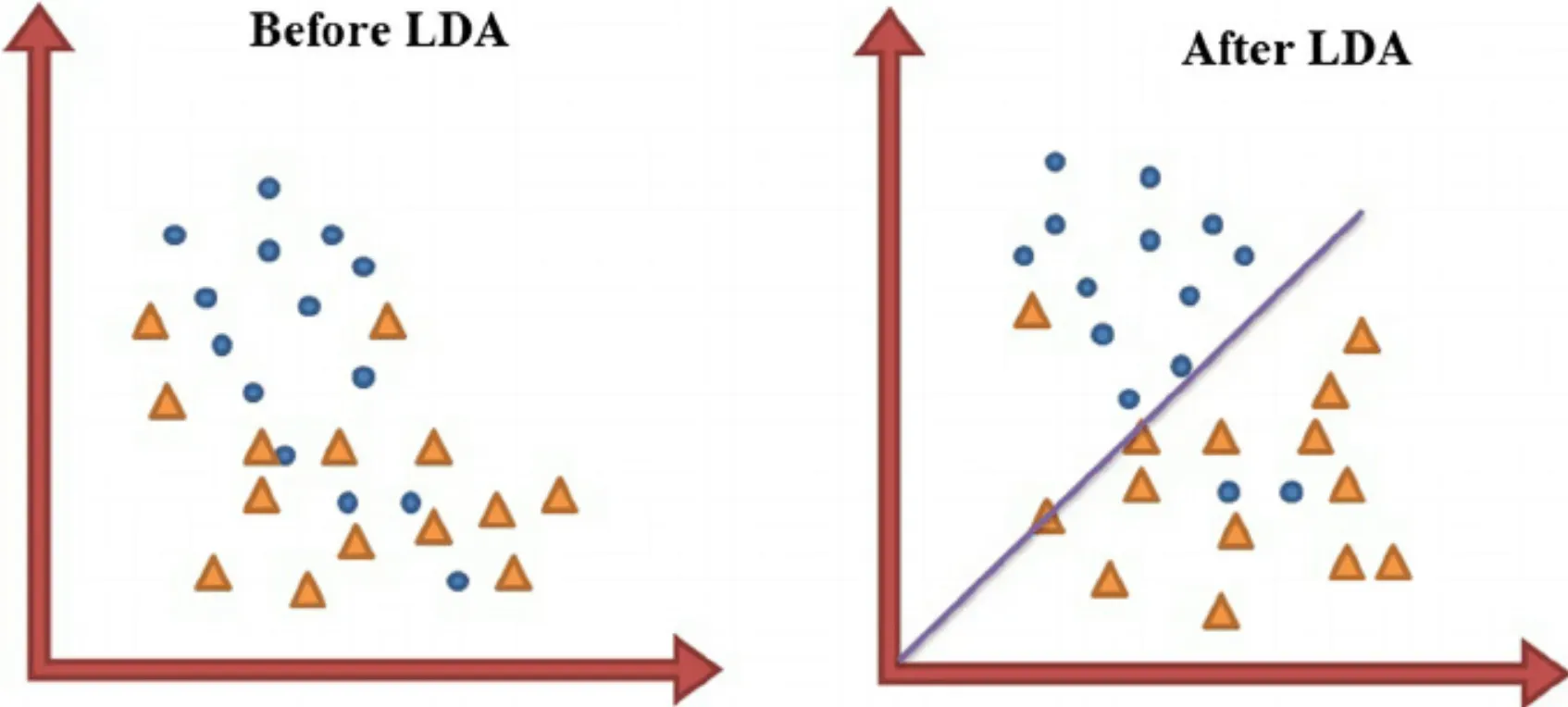
How Linear Discriminant Analysis Works
Ever wondered how LDA performs its magic? Here's the core of it:
- The Algorithm: At a high level, the goal of the LDA algorithm is to project a dataset onto a lower-dimensional space with good class-separability to avoid overfitting.
- Feature Extraction: The LDA method identifies the features (or factors) that account for the most between-group variance in your data.
- Class Separation: LDA aims to maximize the distance between the means of different classes and minimize the variation (scatter) within each class.
- Making Predictions: After the projection is done, predictions are made by projecting input data into the LDA space and using a simple classifier (like Euclidean distance).
Real-life Applications of LDA
LDA has a few real-world applications that are very interesting. Here’s a detailed look:
Facial Recognition

LDA is used in facial recognition technology to find features that separate one face from another.
Medical Diagnosis
In the healthcare industry, LDA is applied for diagnostic classifications based on medical test results or symptoms.
Market Segmentation

In the world of marketing, LDA helps segment customers into separate groups for targeted advertising.
Genomics
In genomics, LDA identifies genes associated with specific conditions or identify relationships between different genes.
Strengths of Linear Discriminant Analysis
Like Superman, LDA has its distinct set of strengths. Here they are.
- Maintains Class Information: LDA, unlike other dimensionality reduction algorithms, uses class labels to maintain more discriminant information.
- Works Well with Small Datasets: LDA can work quite well even when the dataset is small compared to the number of features, something many other algorithms struggle with.
- Multiclass Classification: LDA provides an analytic solution for multiclass classification problems, making it more direct and computationally efficient.
- Robustness: LDA is known for its robustness against variations in the data, meaning it can handle small changes without impacting performance significantly.
Challenges in Linear Discriminant Analysis
No technique is free of challenges, and LDA is no different. But worry not, most can be navigated with a bit of care.
- Assumes Normality: LDA might not work as effectively when data deviate significantly from a normal distribution since it assumes data are normally distributed.
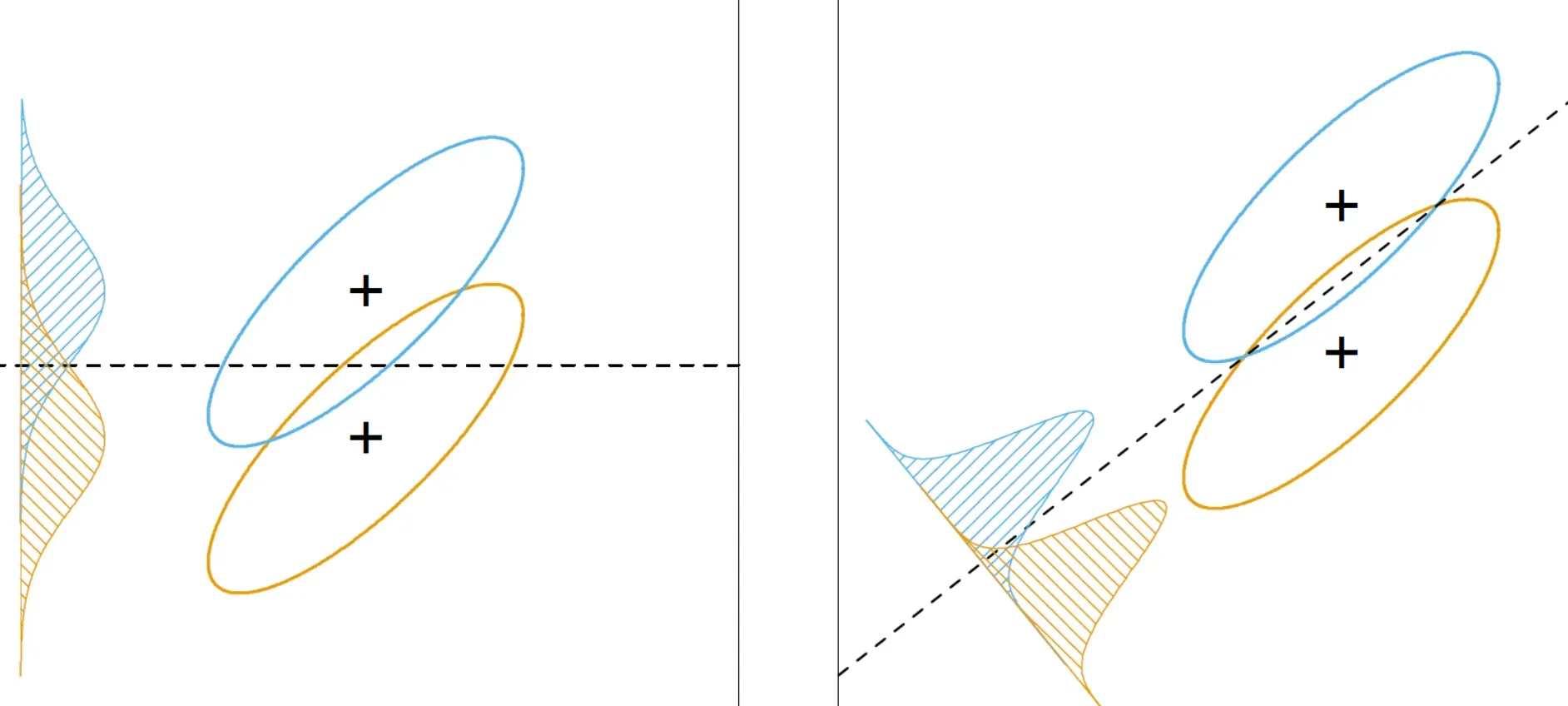
- Identical Covariances: LDA assumes that classes have identical covariance matrices. This might pose a problem when classes differ significantly in terms of covariance.
- Difficulty with Nonlinear Relationships: LDA is a linear method and may not handle nonlinear relationships between variables very well.
- Overemphasis on Outliers: Since LDA is sensitive to outliers, it might sometimes overemphasize their impact on the overall analysis.
Improving Linear Discriminant Analysis
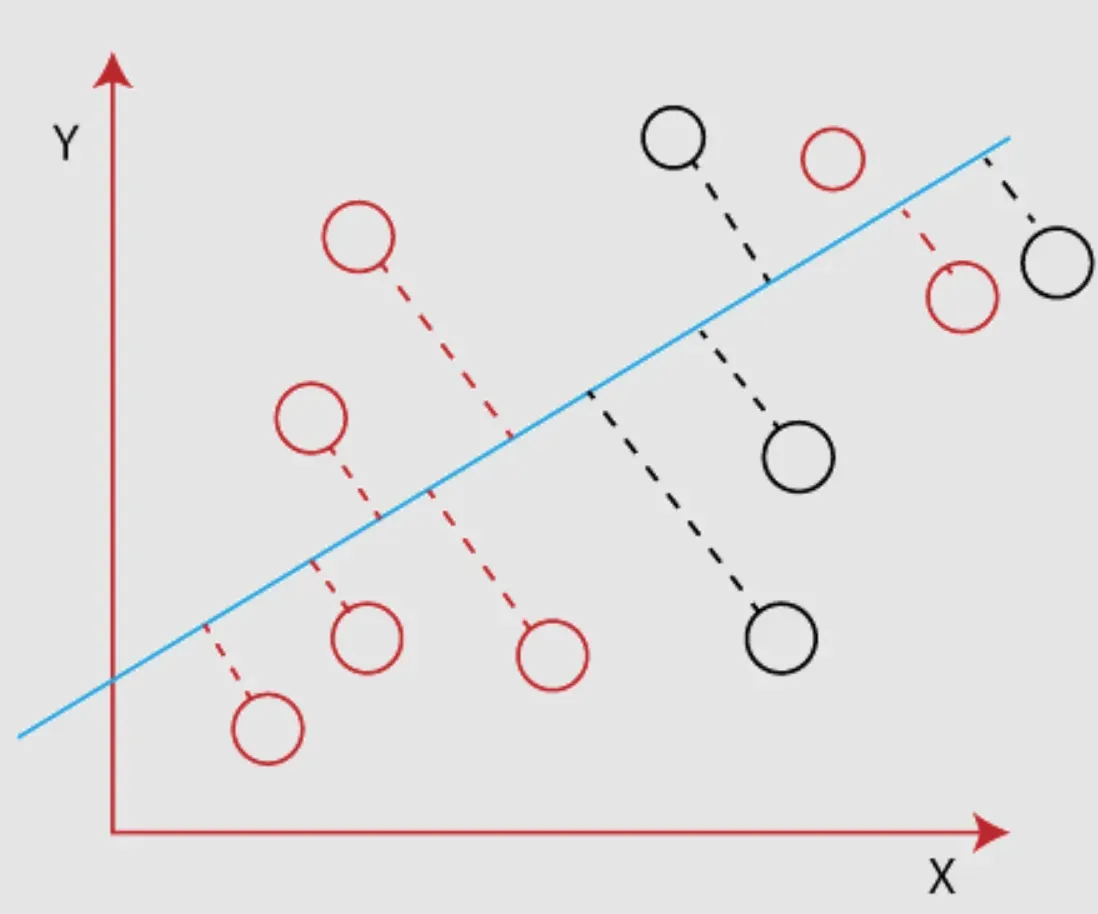
Struggling with LDA? Here are a few tip-offs to improve your analysis.
- Standardization: Before running LDA, it's wise to standardize your variables so they all have the same scale.
- Remove Outliers: Do consider handling outliers in your data as they can have an undue influence on the result of your LDA.
- Verify Assumptions: The assumptions we talked about earlier? Regularly check if they stand true for your data. If not, you might need to tweak.
- Use of Regularization: Regularization methods can be used to reduce overfitting in LDA, thereby boosting its effectiveness.
LDA vs Other Techniques
It's common to wonder how LDA stacks up against other analysis techniques. Here's a crash course.
LDA vs Logistic Regression
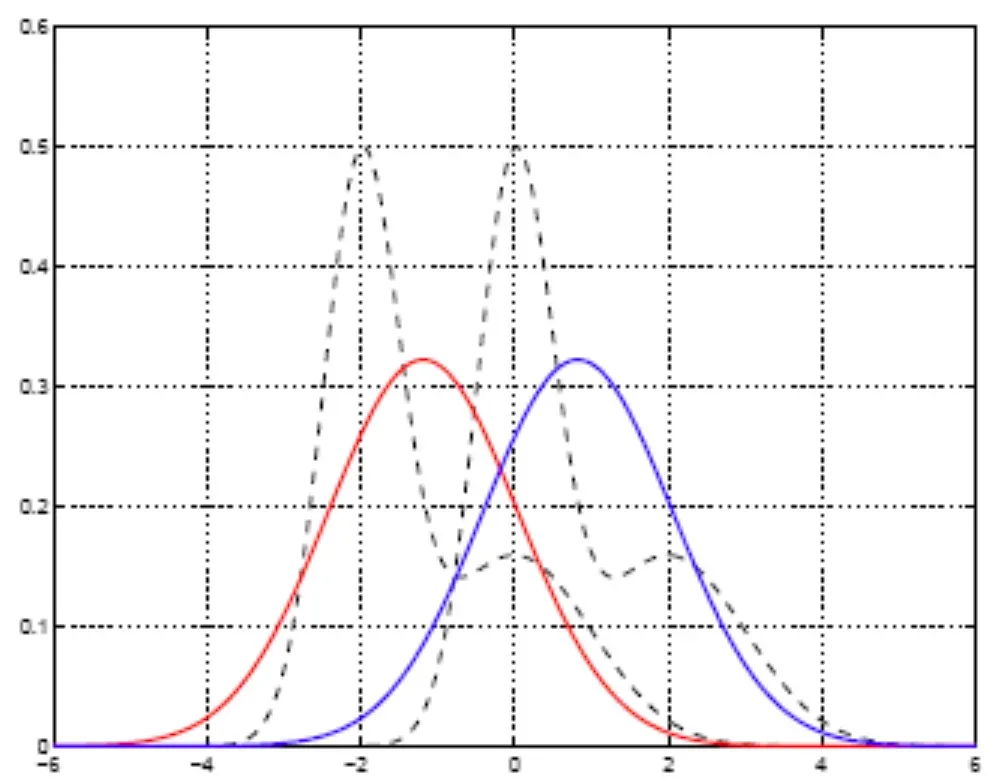
While both are used for classification, LDA assumes normality and equal covariances, logistic regression does not.
LDA vs QDA
Quadratic Discriminant Analysis (QDA) works similarly to LDA but doesn't assume equal covariance matrices.
LDA vs PCA
PCA focuses on explaining the variance in the predictors, rather than maximizing the separation between classes like LDA does.
LDA vs Naive Bayes
LDA assumes that variables are correlated while Naive Bayes assumes that features are independent.
Frequently Asked Questions (FAQ)
What is the main purpose of Linear Discriminant Analysis?
The main goal of LDA is to project a feature space (a dataset n-dimensional samples) onto a smaller subspace while maintaining the class-discriminatory information.
How does LDA differ from PCA?
Both are linear transformation techniques used for dimensionality reduction. PCA is unsupervised and ignores class labels, whereas LDA is supervised and uses class labels to provide more class separability.
What are some common uses of LDA?
LDA can be used for face recognition, customer segmentation, genomics, medical diagnosis, and more.
What are the main assumptions of LDA?
LDA assumes normality, equal class covariances, and independent observations.
What are the strengths and weaknesses of LDA?
Strengths of LDA include maintaining class information, working well with smaller datasets, and robustness against variations.
Challenges include sensitivity to non-normal data, difficulty handling nonlinear relationships, and overemphasis on outliers.