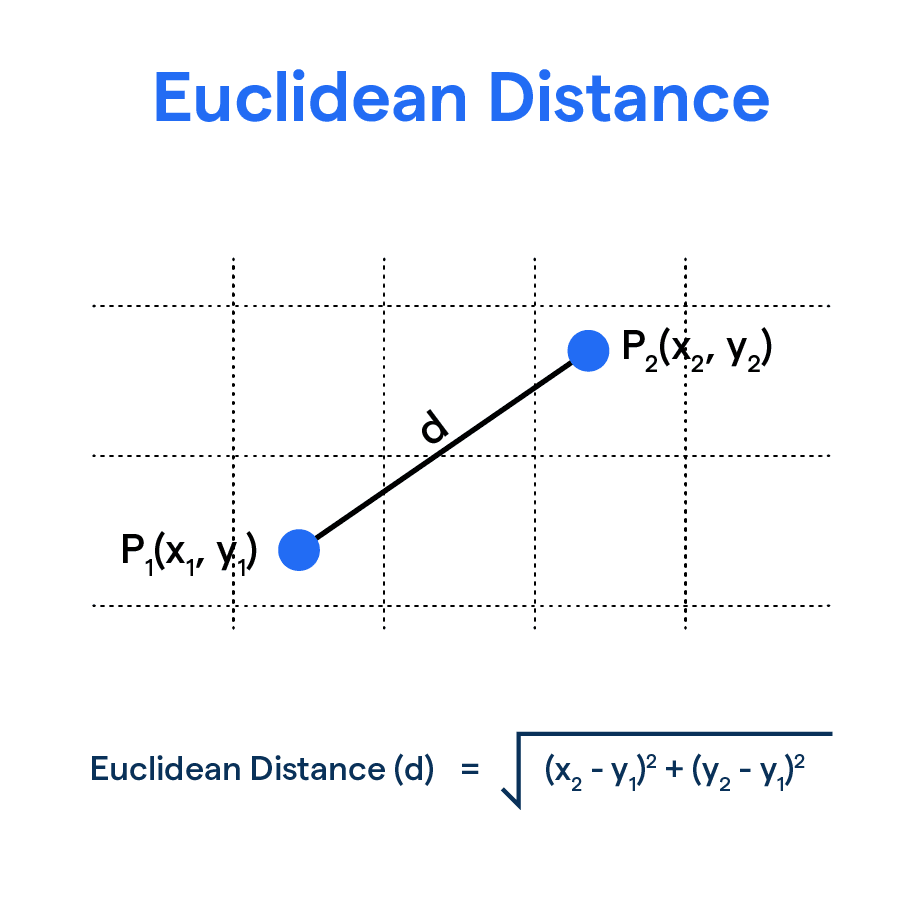
What is Euclidean Distance?
In simple terms, Euclidean distance is a measure of the straight-line distance between two points in a space.
Named after the ancient Greek mathematician Euclid, it's one of the most commonly used methods to calculate distance in fields such as mathematics, physics, and computer science.
Let's use an example. Imagine you're standing at one corner of a room and you want to get to the opposite corner.
The Euclidean distance is the straight line that takes you directly to that corner, like a bird flying from tree to tree.
In a 2-dimensional space, the formula to compute this straight-line distance between two points (say, Point1(x1, y1) and Point2(x2, y2)) is:
√[(x2 - x1)² + (y2 - y1)²]
the Euclidean Distance between two points P1(x1, y1) and P2(x2, y2) in a 3D space is given by the formula:
d(P1,P2) = sqrt[(x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2].
So, the distance will be calculated as the square root of the sum of the squares of differences in both x and y coordinates.
How Does the Euclidean Distance Work and How to Calculate it?
The Euclidean Distance is calculated as follows:
For two points in a 2-dimensional space (Point A: (x1, y1) and Point B: (x2, y2)), Euclidean Distance (d) is given by the formula:
d = √[(x2 - x1)² + (y2 - y1)²]
Now, let's consider some examples along with practical use cases.
- Optimization problems: Let's say we need to find the shortest route for a delivery truck. The depot is at point (0,0) and the delivery point is at (5,10). The Euclidean Distance calculated would be √[(5 - 0)² + (10 - 0)²] = √(25 + 100) = √125 = 11.18 units.
- Space science: For determining the distance between stars. If Star A is at point (2, 2) and Star B is at point (6, 3), the Euclidean Distance would be √[(6 - 2)² + (3 - 2)²] = √(16 + 1) = √17 = 4.12 light years.
- Marketing segmentation: if we have shopper A with a product interest pattern (3, 8, 5) and shopper B with pattern (4, 12, 7), the Euclidean Distance would be √[(4 - 3)² + (12 - 8)² + (7 - 5)²] = √(1 + 16 + 4) = √21 = 4.58, indicating similar shopping preferences.
- Image recognition: Suppose we have two image pixels with RGB values Pixel A: (125, 18, 50) and Pixel B: (130, 20, 60). The Euclidean distance representing color difference is √[(130 - 125)² + (20 - 18)² + (60 - 50)²] = √(25 + 4 + 100) = √129 = 11.36.
- Movie recommendation: For two movies with rating patterns Movie A: (4, 3, 5) and Movie B: (5, 2, 4), the Euclidean Distance would give √[(5 - 4)² + (2 - 3)² + (4 - 5)²] = √(1 + 1 + 1) = √3 = 1.73, implying similar movie ratings.
- Healthcare diagnostics: Comparing medical test results of patient A: (120, 75) (systolic and diastolic blood pressure) and patient B: (130, 80). The Euclidean Distance would be √[(130 - 120)² + (80 - 75)²] = √(100 + 25) = √125 = 11.18, indicating a small difference in the health indicators.
- Social network analysis: To study connectivity in a network graph. If Node A has coordinates (2, 2) and Node B has coordinates (6, 7), the Euclidean Distance would be √[(6 - 2)² + (7 - 2)²] = √(16 + 25) = √41 = 6.40.
Why Do We Need Euclidean Distance?
In this section, we'll cover the importance and practical applications of Euclidean Distance, it’s one of the fundamental concepts used in mathematics and several scientific fields for analyzing distance.
The Foundation of Geometry
Euclidean distance, coming from Euclidean geometry, forms the backbone of classical geometric principles.
The concept applies to objects in two-dimensional, three-dimensional, or higher-dimensional spaces, making it universally applicable whenever there's a need to measure 'straight-line' distance.
Machine Learning Algorithms

Euclidean distance is of paramount importance in machine learning and data science.
It's used in algorithms like K-Nearest Neighbors, K-Means, and Principal Component Analysis, which rely on distance computation to classify data points, identify clusters, or reduce dimensions.
Image Processing and Computer Vision
In computer vision and image processing, Euclidean distance plays a key role in comparing and contrasting images.
It helps in tasks like pattern recognition, similarity checks, and object detection, contributing to applications such as facial recognition or autonomous vehicles.
Spatial Analysis and GIS Systems
In Geographic Information System (GIS) and spatial analytics, Euclidean distance helps calculate actual geographical distances and execute spatial operations such as map-matching, route planning, or area selection.
Enhancing User Experience
Finally, in the context of enhancing user experience in digital services, Euclidean distance is used to personalize services.
For example, in recommender systems, it helps in determining the 'closeness' or similarity between the preferences or behavior patterns of different users, allowing systems to provide recommendations that are more likely to resonate with the user.
Euclidean Space and Geometry
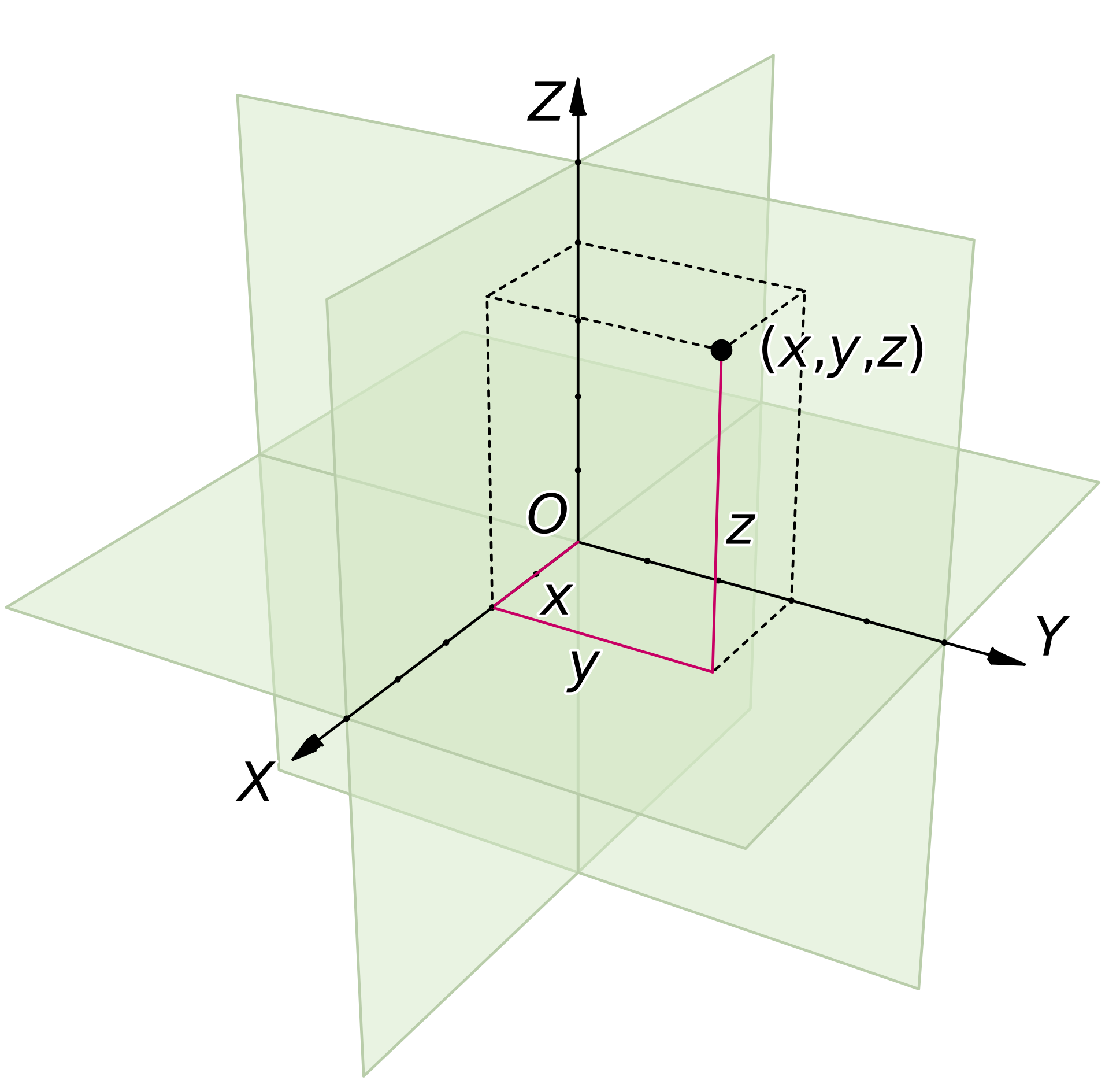
In this section, we will delve into key aspects of Euclidean space and related geometrical concepts.
Euclidean space, named after the ancient Greek mathematician Euclid, is the fundamental space of geometry.
It's composed of points and can be intuitively thought of as a multi-dimensional generalization of the familiar two or three-dimensional space.
Euclidean Geometry
Euclidean Geometry is a mathematical system attributed to Euclid's work "Elements". It encompasses the study of plane and solid figures based on axioms and theorems employed by Euclid.
Fundamental concepts include points, lines, angles, and circles.
Coordinate Systems
In Euclidean space, a coordinate system allows every point to be specified by a finite list of real numbers - the coordinates of the point.
The most common are Cartesian and polar coordinate systems.
Distance in Euclidean Space
The notion of distance is a key component in Euclidean space, with the common measurement method being Euclidean Distance. It represents the "straight line" distance between two points.
The Impact of Euclidean Space
Euclidean space and geometry are foundational to many mathematical and scientific fields, including physics, engineering, computer science, and data science.
The conceptual framework it provides continues to play a significant role in understanding the world around us.
Key Concepts with Euclidean Distance
Euclidean Distance is used in several contexts, but there are three prime terms you should know about in reference to Euclidean Distance.
Euclidean Distance in the context of Raster Analysis
This term is used in raster analysis to measure the Euclidean distance between any cell and the nearest cell that satisfies a certain criterion.
Euclidean Allocation: Determining Proximity for Allocation
Euclidean Allocation is a term used in location allocation modeling. It refers to the process of determining proximity criteria for allocating resources to different locations.
Euclidean Direction: Finding Direction to the Nearest Source
Euclidean Direction is used to assess the direction of the nearest source from the given point. It helps determine the closest location to a given point in a network.
Calculation Examples
Let's take a look at some examples to fully understand how Euclidean Distance is calculated.
Consider two points P1 (2, 3) and P2 (5, 6). The Euclidean Distance between the two points using the formula is:
d(P1,P2) = sqrt[(5 - 2)^2 + (6 - 3)^2]
= sqrt[9 + 9]
= sqrt(18)
= 4.24 (approx)
Advantages and Limitations of Euclidean Distance
In this section, we'll cover the primary advantages and limitations of utilizing Euclidean Distance.
Advantages
Various advantages of Euclidean Distance-
- Simplicity and Ease of Interpretation: One of the biggest advantages of Euclidean distance is its simplicity.
The calculation is straightforward and intuitive, representing the most direct path between two points. This also makes it easy to interpret and understand.
- Applicability across Dimensions: Euclidean distance can be applied across different dimensions - be it two, three, or more.
This makes it highly versatile for a wide range of multi-dimensional data analysis tasks across varied domains.
Limitations
Various limitations of Euclidean Distance-
- Sensitivity to Scaling: Euclidean distance can be significantly impacted by the scale or units of measurement of the data.
This means that if variables are not in the same units or their scales are not normalized, the distance calculation may be skewed.
- Inadequate for High-Dimensional Data: As the dimensionality of the data increases, Euclidean distance tends to become less effective, a phenomenon known as the "curse of dimensionality".
In high-dimensions, distances between most pairs of points start to look similar, reducing the discriminatory power of Euclidean distance.
- Ignorance of Correlation or Dependence: Euclidean distance treats each dimension separately and doesn't account for any potential correlation or inter-dependencies that might exist among the dimensions.
While the Euclidean distance's simplicity and ease of implementation make it a popular choice for measuring distance, it's important to consider its limitations like sensitivity to scaling, reduced effectiveness in high dimensions and lack of accounting for inter-variable correlations.
Frequently Asked Questions (FAQs)
What is Euclidean Distance?
Euclidean Distance is a measure of the straight-line distance between two points in Euclidean space. It is calculated using the Pythagorean theorem.
What are the applications of Euclidean Distance?
Euclidean Distance has a wide range of applications in various fields such as machine learning, optimization theory, computer vision, and exercise motion capture.
How is Euclidean Distance calculated?
In a 2D space, Euclidean Distance between two points P1(x1, y1) and P2(x2, y2) is calculated using the formula: d(P1,P2) = sqrt[(x2 - x1)^2 + (y2 - y1)^2]. It is similar for 3D space.
What are the key concepts related to Euclidean Distance?
Euclidean Distance is used in several contexts. Some of the key concepts are Euclidean Distance in the context of raster analysis, Euclidean allocation, and Euclidean direction.
What are the advantages and limitations of Euclidean Distance?
Euclidean Distance is simple to compute and conforms to the Pythagorean theorem. But it assumes that the surface between two points is flat, which isn't always accurate.