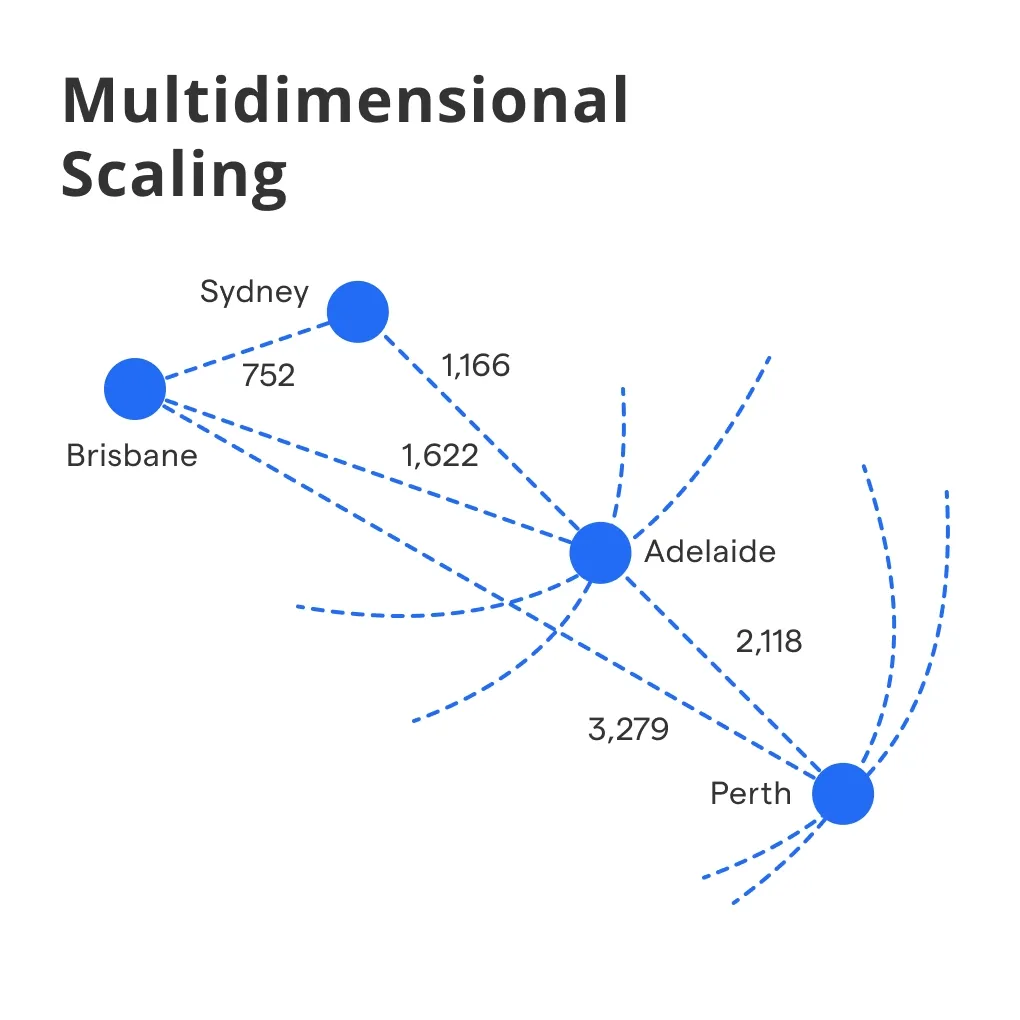
What is Multidimensional Scaling?
Multidimensional Scaling (MDS) is a means of visualizing the level of similarity of individual cases of a dataset. It refers to a set of statistical techniques used for exploratory data analysis and dimension reduction.
Components of Multidimensional Scaling
The major components which together constitute Multidimensional Scaling include input data, distance algorithm, and dimensionality output.
Uses of Multidimensional Scaling
Common applications of Multidimensional Scaling stem from fields such as information technology, marketing research, and social and psychological research, among others.
Types of Multidimensional Scaling
There are two main types of MDS— metric (also known as classical or Torgerson scaling) and nonmetric. These two types emphasize on recovery of the distance structure and the order structure, respectively.
Associated Terms
Some terms closely associated with MDS include dimensionality reduction, data visualization, dissimilarity matrix, and similarity mapping.
Why is Multidimensional Scaling Used?
This section probes the various reasons why Multidimensional Scaling is employed as a method in data analysis.
Simplicity in Visualizing Complexity
Multidimensional Scaling enables researchers to distill complex, multi-dimensional data sets into a format that’s easier to visualize and understand. The technique’s output is a simple scatter plot.
Versatility
MDS can be used with any type of data, as long as a distance or dissimilarity measure can be calculated, making it quite versatile.
Preservation of Data Structure
Multidimensional Scaling reduces dataset dimensionality while preserving the structure of the data, allowing users to perceive patterns and clusters.
Enhanced Data Interpretation
MDS can aid in the discovery of dimensions that distinguish different categories of data points, enhancing analysts' understanding of data.
Handling of Missing Data
MDS uses an iterative approach to handle missing data, as opposed to listwise deletion or mean substitution.
Who Uses Multidimensional Scaling?
Various professional domains find Multidimensional Scaling beneficial for their operations.
Psychologists
Psychologists use MDS to understand perceptual dimensions on scales such as the similarity of stimuli.
Market Researchers
Market researchers employ MDS to compare brands or products based on consumer perceptions or preferences.
Technology and Data Analysts
People in these roles use MDS for dimension reduction in order to visualize complex, multi-dimensional data on a scatter plot.
Social Scientists
Social scientists employ MDS to visualize differences and similarities in survey data, typically working with large datasets.
Environmental Researchers
In environmental research, MDS is used to study similarities and differences in different ecosystems or habitats.
When is Multidimensional Scaling Used?
Multidimensional Scaling is used under certain conditions which are explained in this section.
Dealing with Multi-Dimensional Data
MDS is used when a dataset contains multiple attributes that cannot be easily visualized on a two or three-dimensional plane.
For Exploratory Data Analysis
MDS is ideally suited for the initial, exploratory phase of data analysis when the aim is to discover underlying patterns or data structures.
Evaluating Consumer Preference
Companies or researchers may use MDS to understand consumer preferences when they want to evaluate how different products or brands are perceived.
Need for Data Simplification
When the data is complex and analysts need to simplify it into a form that is easier to understand and communicate, MDS proves helpful.
Comparing Different Entities
MDS is deployed in scenarios when the distance or dissimilarity between different entities needs to be visualized.
How is Multidimensional Scaling Implemented?
Now let's review the methodology involved in applying Multidimensional Scaling.
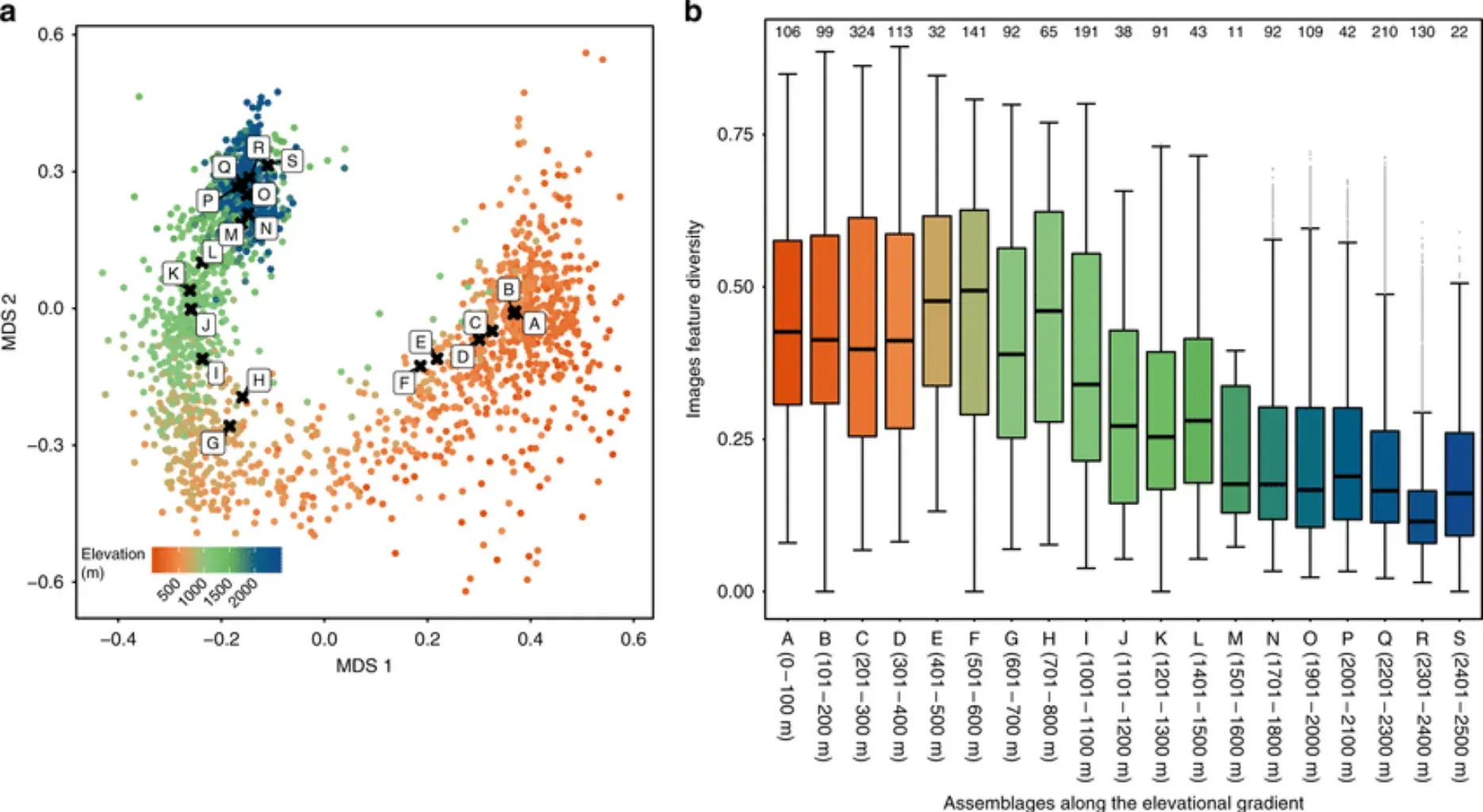
Procuring Initial Data
The process of implementing MDS begins with the collection of data, often in the form of a dissimilarity matrix.
Computing Dissimilarity or Distance Matrix
The computation of the dissimilarity or distance matrix based on the attributes of the objects under study is the next step.
Determining Number of Dimensions
The number of dimensions that would best represent the data is decided based on stress values or another criterion.
Configuring Initial Plot
An initial configuration is formed, and distances in this initial configuration are calculated.
Iterative Procedure
The coordinates are adjusted iteratively with the goal of improving the goodness-of-fit between the original and the transformed data.
What are the Assumptions in Multidimensional Scaling?
Even though MDS is versatile, certain assumptions are made while using this technique.
Assumption of Scale Level
MDS assumes that the input measures are consistent with at least ordinal scaling, i.e., the objects can be arranged in some order.
Distances are Euclidean
It is typically assumed that the distances are Euclidean - particularly in metric MDS. However, this assumption can be relaxed in nonmetric MDS.
Assumption of Independence
MDS usually assumes that the dissimilarities are independent of each other and have similar variances.
Symmetry of Distances
MDS often assumes that the distances are symmetric in the sense that the distance from A to B is the same as the distance from B to A.
Marathon Runner Assumption
MDS assumes that shorter paths are preferred over long ones (just as a marathon runner would take the shortest path). This assumption is implicit in the use of regular Euclidean distances.
Best Practices in Multidimensional Scaling
Following certain best practices can help in the effective implementation of MDS.
Make Selection of Distance Measure Clear
The selection of an appropriate distance measure is crucial for achieving meaningful results.
Conduct Dimensionality Checks
The number of dimensions to represent the data should be chosen carefully, ensuring it is neither too little (leading to loss of information) nor too many (making interpretation difficult).
Check for Outliers
Outliers can distort the MDS map, so it is good practice to check the data for outliers before using MDS.
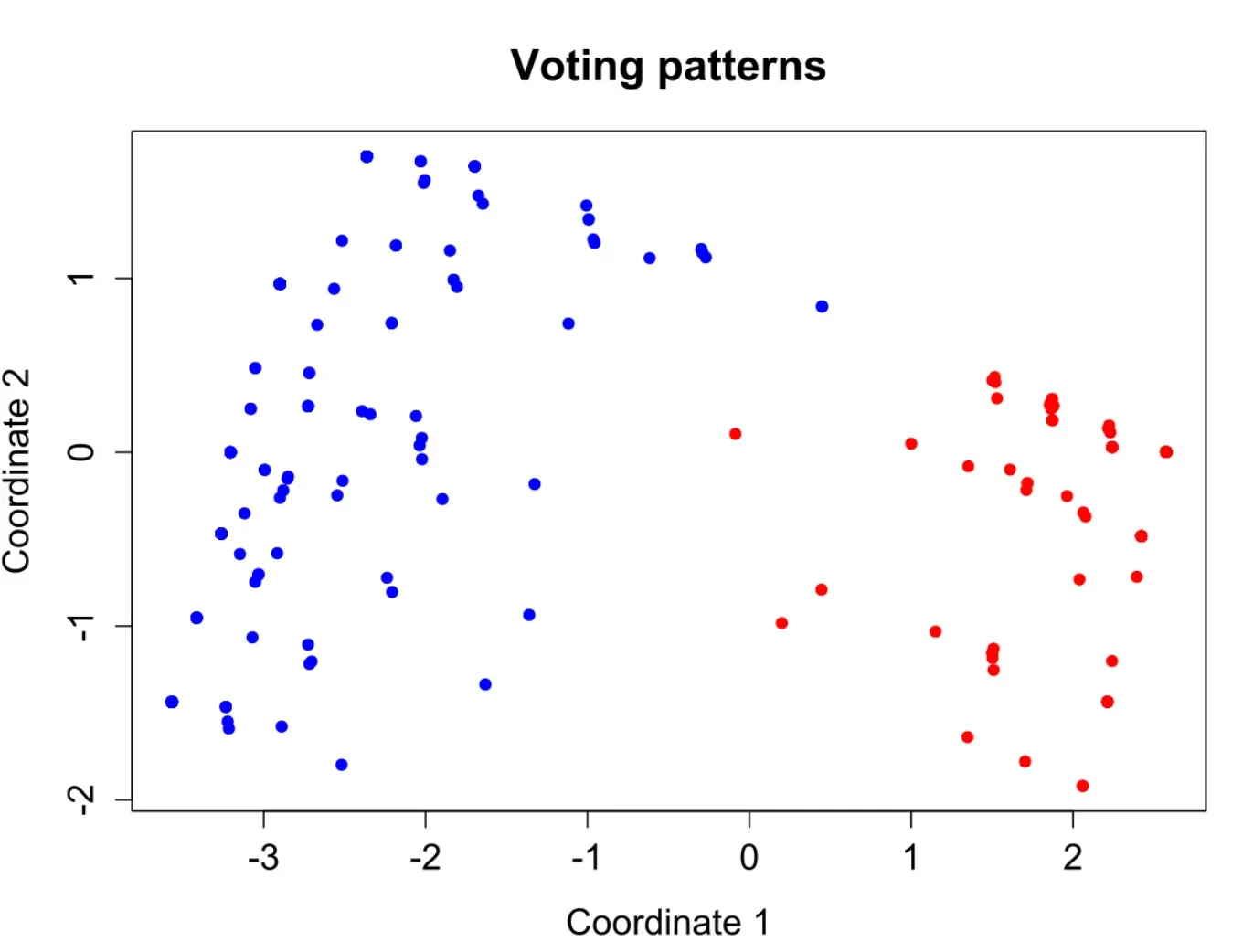
Interpret Directions and Clusters but Not Locations
In MDS plots, the focus should be on the direction and relative distances between points, not their exact location since it is arbitrary.
Replicate Analysis with Different Seed Values
Running the analysis with different seed values helps ensure the solution obtained is not a local but a global solution.
Challenges in Multidimensional Scaling
Several challenges exist in the practical application of MDS.
Difficulty in Interpretation
Interpretation of the dimensions in an MDS solution can sometimes be difficult and subjective.
Distortion of Spaces
Determining the appropriate number of dimensions is challenging and can lead to errors.
Robustness Issues
MDS may not be robust to high levels of measurement error.
Assumption Violation
Real data often violate the assumptions of MDS which can impact the accuracy of the result.
Computational Complexity
MDS requires significant computation, especially when dealing with large datasets.
Trends in Multidimensional Scaling
Finally, let’s take a glance at the ongoing trends in MDS.
Integration with Machine Learning
MDS technique is being integrated with machine learning algorithms to develop hybrid models for better data visualization and prediction.
Dealing with Big Data
MDS algorithms are being adapted to effectively handle massive, complex datasets.
Non-Euclidean Distances
Increasing use of non-Euclidean distances is observed for situations where distance does not reflect similarity.
Dynamic MDS
Dynamic MDS, suitable for time-series data where the position of the points changes over time, is being used more frequently.
Quantum MDS
Researchers are exploring the application of quantum algorithms to perform MDS in an effort to reduce computation time and increase efficiency.
In conclusion, Multidimensional Scaling is a well-established tool for dealing with multi-dimensional data. It provides a useful way to visualize patterns in complex data, contributing to understanding and communication. However, proper application of MDS requires a good understanding of its principles, assumptions, and potential pitfalls.
Nonetheless, with ongoing advances and trends, its adaptation and further development are likely to continue, making it an even more useful tool in the analysis and interpretation of multi-dimensional data.
Frequently Asked Questions (FAQs)
How Can Multidimensional Scaling Benefit Data Visualization?
Multidimensional Scaling (MDS) simplifies high-dimensional data into a lower-dimensional space, making it easier to visualize and understand.
How Does Stress Measure the Effectiveness of MDS?
Stress quantifies the difference between actual distances in high dimensions and those in the reduced space, indicating the quality of MDS.
Can MDS Help in Clustering Analysis?
Yes, MDS can simplify clustering by reducing dimensionality while preserving relative distances, aiding in revealing underlying structures in the data.
Does the Choice of Distance Metric Impact MDS?
The choice of distance metric significantly impacts MDS outcomes, as it determines how dissimilarities between data points are calculated in the high-dimensional space.
How Does MDS Manage Non-Euclidean Distances?
MDS can handle non-Euclidean distances, making it ideal for cases where data does not follow typical Euclidean geometry (e.g., geographical or graph data).