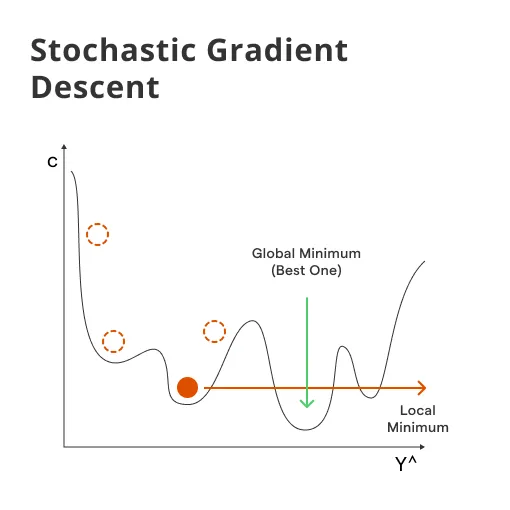
What is Stochastic Gradient Descent?
Let's start by breaking Stochastic Gradient Descent down to its fundamentals.
Definition
Stochastic Gradient Descent (SGD) is an iterative method used in machine learning and optimization to find the best parameters for a model in order to minimize the objective function, primarily when dealing with large datasets.
Role in Machine Learning
In the context of machine learning, stochastic gradient descent is a preferred approach for training various models due to its efficiency and relatively low computational cost.
Operation
SGD optimizes parameters by iteratively adjusting them to minimize the result of a particular loss function.
Applicability
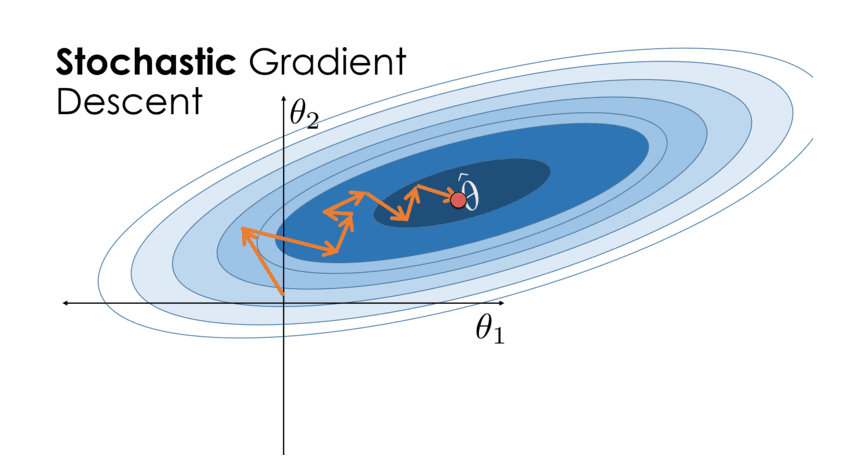
While applicable to many optimization problems, SGD is particularly suited for those with large-scale, high-dimensional data or functions that are too complex for analytical solutions.
Intuition
Imagine standing at the top of a high mountain with the aim of reaching the sea level.
SGD is like taking steps downwards depending on the steepness of the slope, adjusting your direction based on the terrain encountered, rather than the entire landscape.
Why is Stochastic Gradient Descent Important?
Let's discuss why Stochastic Gradient Descent is an integral part of machine learning and optimization.
- Efficiency: SGD, by updating parameters on a per-sample basis, performs notably faster than batch gradient descent, which calculates the gradient using the whole dataset.
- Scalability: SGD is ideal for datasets too large to fit in memory since it only requires one training sample at a time, promoting scalability.
- Flexibility: SGD can work with any loss function that is differentiable, giving it flexibility across a range of machine learning problems.
- Noise Handling: Being stochastic in nature, SGD is good at escaping shallow local minima in the loss landscape, thus often finding better solutions in a non-convex setting.
- Regularization: SGD, combined with certain types of regularization (such as L1 or L2 regularization), can help prevent overfitting of the model.
Who Uses Stochastic Gradient Descent?
Next, let's identify the key players who frequently use Stochastic Gradient Descent in their tasks.
- Data Scientists: Data scientists dealing with large-scale, high-dimensional data often use SGD as a primary tool for model optimization and predictive analytics tasks.
- Machine Learning Engineers: For machine learning engineers, SGD is a fundamental tool that is applied across various learning models, including linear regression, SVMs, and neural networks.
- AI Researchers: Researchers investigating AI algorithms utilize SGD as a pivotal step in the development and refining of complex models.
- Statistical Analysts: Those involved in predictive modeling or optimization in areas like economics and finance also adopt SGD due to its robustness and scalability.
- Software Developers: Software developers building Machine Learning applications with large datasets harness SGD's power to ensure effective and efficient model training.
When is Stochastic Gradient Descent Used?
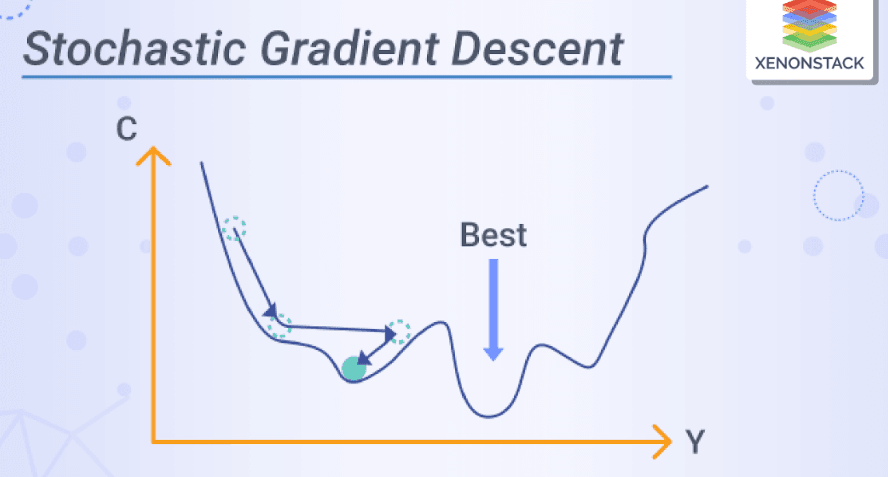
To better understand its applications, we need to discuss when and in what scenarios Stochastic Gradient Descent is applied.
- Large Datasets: SGD shines when dealing with very large datasets that are too computationally expensive for batch gradient descent.
- Complex Models: For training complex models such as deep learning networks, SGD and its variants (like Mini-batch SGD) are often employed.
- Non-Convex Problems: In non-convex optimization scenarios where multiple minimums exist, the stochastic nature of SGD helps to escape shallow minima.
- Real-Time Applications: SGD is ideal for real-time or online learning scenarios where data arrives in a sequential manner, and the model needs to be updated on the go.
- Resource-Constrained Environments: In situations where computational resources are limited, the efficiency of SGD makes it a suitable choice for model optimization.
Where in the Algorithm is Stochastic Gradient Descent Implemented?
Grasping where SGD fits into a machine learning algorithm can shed light on how it works.
- Model Parameter Optimization: SGD is employed in the optimization step where model parameters are fine-tuned to minimize the loss function.
- Training Loop: Within the training loop, SGD updates the model's parameters after calculating the gradient of the loss function with respect to a random training sample.
- Weight Updates: In neural networks, SGD is used for weight updates, adjusting neuron connection strengths to improve the model's predictive performance.
- Gradient Calculation: Each iteration of SGD involves the calculation of gradients, which determine how to adjust the model's parameters.
- Convergence Check: SGD is involved until the algorithm convergence criteria are met, i.e., until the changes in the loss function fall beneath a small, defined threshold.
How is Stochastic Gradient Descent Implemented?
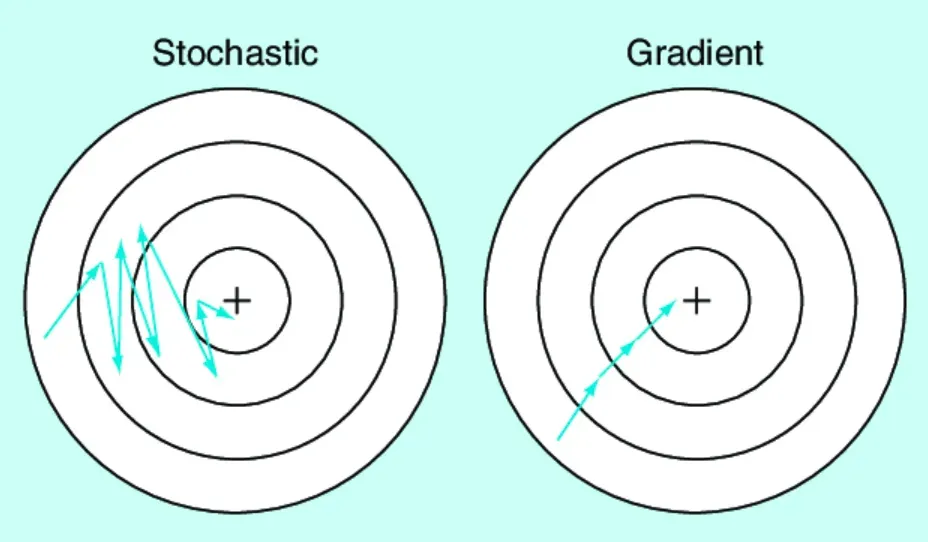
Unravel the algorithmic process behind Stochastic Gradient Descent implementation.
- Initialization: First, the model parameters are initialized randomly or with some predetermined values.
- Sample Selection: In each iteration, a random sample is selected from the training dataset.
- Gradient Calculation: The gradient of the loss function with respect to the parameters is calculated using the selected sample.
- Parameter Update: The parameters are updated in the opposite direction of the gradient, with the magnitude of the change proportional to the learning rate and the gradient.
- Iterative Process: Steps 2-4 are repeated until the algorithm has either run a predefined number of iterations or the change in loss becomes negligibly small.
Conceptual Underpinnings of Stochastic Gradient Descent
Getting to the conceptual foundations of Stochastic Gradient Descent can help appreciate the method's working.
Learning Rate
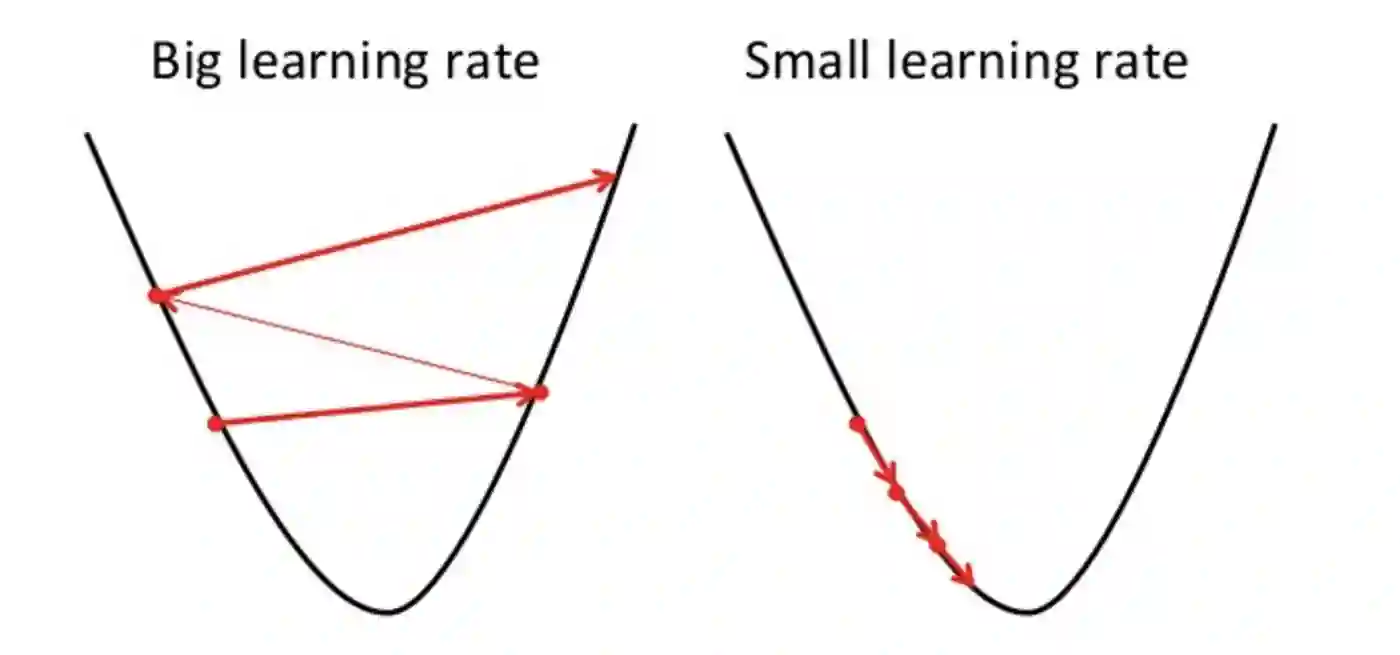
The learning rate is a vital hyperparameter that decides how much the parameters should be updated in each iteration.
Loss Function
The choice of the loss function depends on the problem at hand, and it plays a pivotal role in the effectiveness of SGD.
Convergence Criteria
Deciding the termination condition is critical to avoid overfitting or underfitting and achieve a reliable model.
Regularization
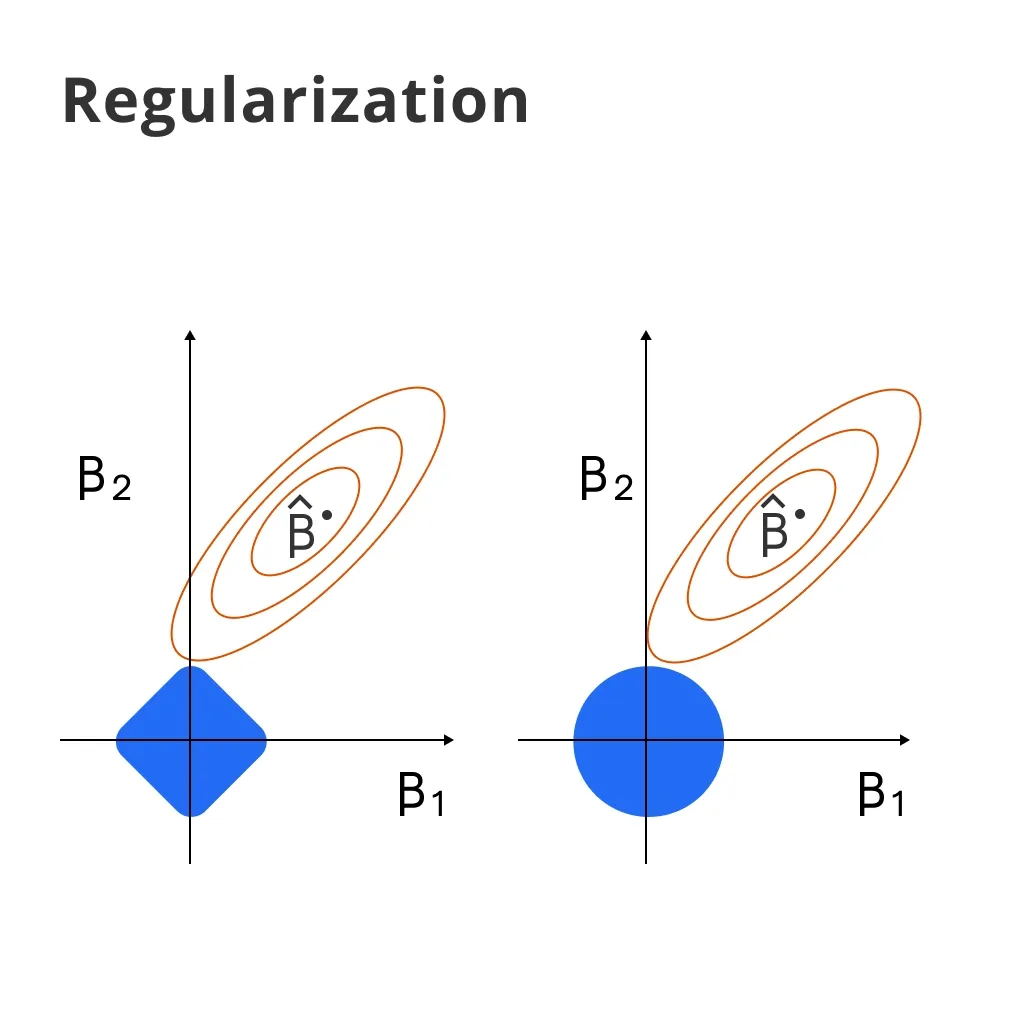
Options for regularization methods like L1 and L2 can be integrated into SGD to prevent overfitting.
Mini-Batch SGD
A variant of SGD, mini-batch SGD, uses a small number of random samples in each iteration, achieving a balance between computational efficiency and gradient estimation accuracy.
Coding Stochastic Gradient Descent
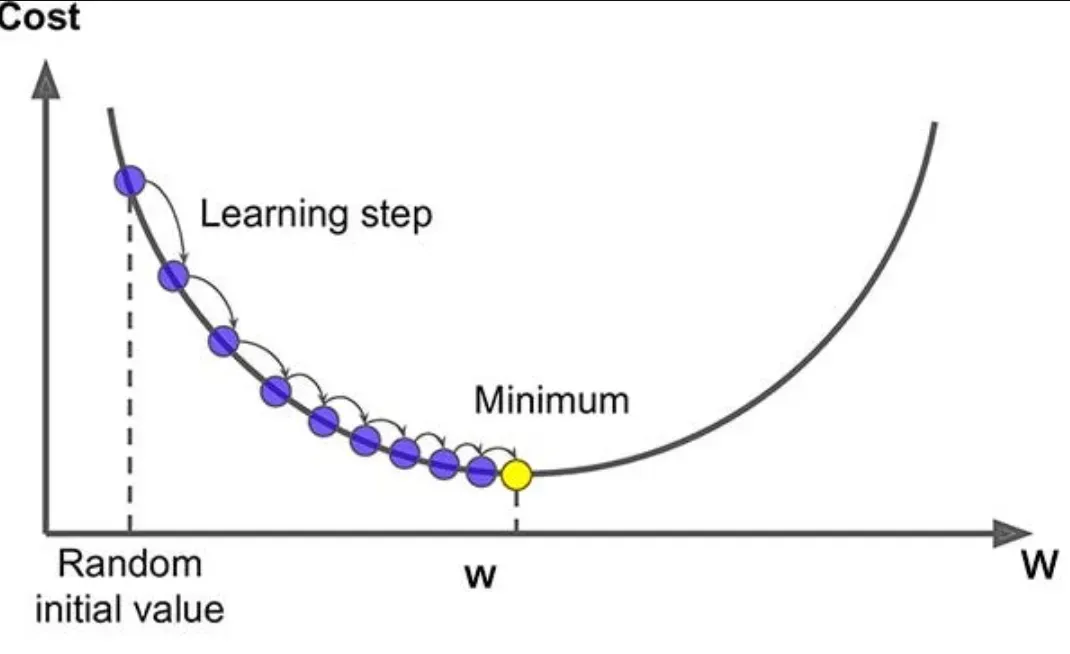
A brief look into coding Stochastic Gradient Descent gives a practical feel of its implementation.
- Language Preference: Most commonly, languages such as Python, R, or MATLAB are used to code SGD due to their rich libraries and tools.
- Libraries and Tools: Libraries like NumPy, Scikit-learn, TensorFlow, and PyTorch in Python offer built-in functions for SGD and are extensively used in machine learning tasks.
- Customization: One can code SGD from scratch for granular control and a deeper understanding of the algorithm.
- Debugging and Testing: Thorough testing and debugging of your SGD implementation is necessary to ensure its correctness and efficiency.
- Platform Choice: Platforms like Jupyter notebooks, Colab, Kaggle, or local Integrated Development Environments (IDEs) are usually preferred for model training involving SGD.
Beyond Basic Stochastic Gradient Descent
Having understood SGD, let's discuss its advanced variants and how they can enhance performance.
Momentum
SGD with momentum takes into account the previous gradients to smoothen the convergence by reducing oscillations.
Nesterov Accelerated Gradient
This is a variant of momentum which provides a better approximation to the gradient at the new position leading to faster convergence.
AdaGrad
AdaGrad adapts the learning rate to the parameters, performing larger updates for infrequent parameters and smaller updates for frequent ones.
RMSProp
RMSProp adjusts the Adagrad method in a way that it works well in online and non-convex settings by using a moving average of squared gradients.
Adam
A combination of RMSProp and Momentum, Adam is a widely used optimization method that computes adaptive learning rates for each parameter.
Best Practices for Stochastic Gradient Descent
To ensure optimal outcomes while utilizing Stochastic Gradient Descent, several practices are generally recommended.
Learning Rate Scheduling
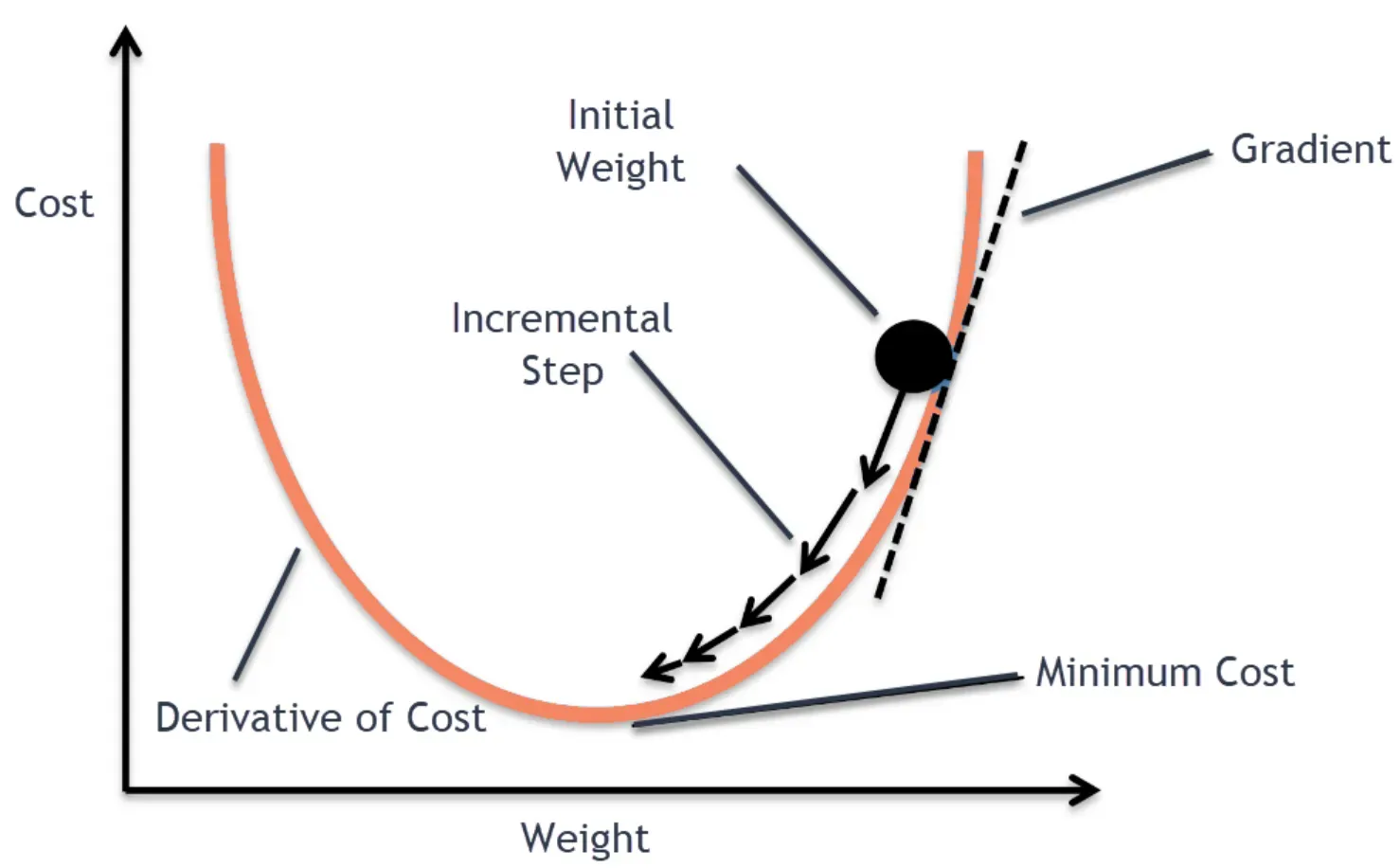
The learning rate is a critical hyperparameter that controls the step size during the optimization process. Setting it too high can cause the algorithm to oscillate and diverge; too low can result in slow convergence.
It might initially be large, to make quick progress, but gradually decreased to allow more fine-grained parameter updates to reach the optimal solution.
Examples of learning rate scheduling include:
- Step-based decay: The learning rate is reduced by a factor after a predefined number of epochs.
- Exponential decay: The learning rate decreases at an exponential rate throughout training.
- 1/t decay: The learning rate decreases in proportion to the inverse of the square root of the number of iterations.
- Adaptive learning rate methods: Methods such as AdaGrad, RMSProp, or Adam adaptively adjust the learning rate.
Regularization Techniques
Regularization prevents overfitting by adding a penalty term to the loss function that discourages complex or unstable models.
Examples of regularization techniques include:
- L1 (Lasso) regularization: It encourages sparsity (fewer parameters) by adding the absolute values of the weights to the loss function.
- L2 (Ridge) regularization: It prevents any weight from becoming overly dominant by adding the squares of the weights to the loss function.
- Dropout: In deep learning, it randomly turns off a proportion of neurons during each training iteration, promoting weight sharing and improving generalization.
Batch Normalization
In deep learning, batch normalization can make SGD more stable and robust by normalizing the activation outputs of each layer.
Early Stopping
This strategy involves monitoring the model's performance on a validation set and stopping the training when the error begins to increase (a sign of overfitting).
Challenges with Stochastic Gradient Descent
Despite its prowess, there are several challenges to using Stochastic Gradient Descent.
Hyperparameter Tuning
Choosing appropriate values for hyperparameters like learning rate, batch size, or the regularization term can significantly influence the algorithm's performance but can be complex and time-consuming.
Saddle Points and Local Minima
SGD can sometimes get stuck in saddle points (regions where some dimensions slope up and some slope down) or local minima (regions not the global best).
Vanishing and Exploding Gradients
In deep networks, gradients can become very small (vanish) or very large (explode) as they are backpropagated, making it hard to effectively update the weights.
Slow Convergence
SGD can be slower to converge than batch gradient descent because it makes frequent updates with high variance.
Stochastic Gradient Descent in Future Perspective
Finally, looking into the future role of Stochastic Gradient Descent in machine learning and artificial intelligence landscapes.
- Continual Learning: SGD's utilities in online and real-time learning situations make it well-suited to future applications requiring continuous learning.
- Deep Learning Advancements: As deep learning techniques continue to develop and gain complexity, SGD and its variants will remain foundational to training these models.
- Big Data Settings: The rise in big data will ensure SGD's relevance due to its efficiency and scalability with large datasets.
- Reinforcement Learning: Reinforcement learning, a rapidly evolving field in artificial intelligence, often involves optimization methods including SGD.
- Unsupervised Learning: The growing interest in unsupervised learning scenarios may generate novel ways and variants of SGD to optimize such models effectively.
Frequently Asked Questions (FAQs)
How does Stochastic Gradient Descent differ from Standard Gradient Descent?
Unlike standard Gradient Descent that uses the whole data batch for each update, Stochastic Gradient Descent (SGD) updates parameters for each training example one at a time, making it faster and enabling online learning.
Why is Stochastic Gradient Descent often preferred in Machine Learning?
SGD’s ability to iterate quickly through training samples makes it a preferred choice in situations where the data is too large to process in memory or computation is a constraint.
What is Mini-Batch Gradient Descent?
Mini-Batch Gradient Descent, a variation of SGD, combines the advantages of both SGD and Batch Gradient Descent. It updates parameters using a mini-batch of ‘n’ training examples, striking a balance between computational efficiency and convergence stability.
How can the learning rate affect SGD Performance?
The learning rate in SGD determines the size of steps taken towards minimum. Small learning rates ensure accurate convergence but may be slow.
Larger rates speed up the process, but risk overshooting the minimum.
What is momentum in the context of SGD?
Momentum in SGD is a technique that helps accelerate gradient vectors in the right direction, leading to faster convergence. It works by adding a fraction of the update vector from the previous step to the current step.