Introduction to Softmax Function
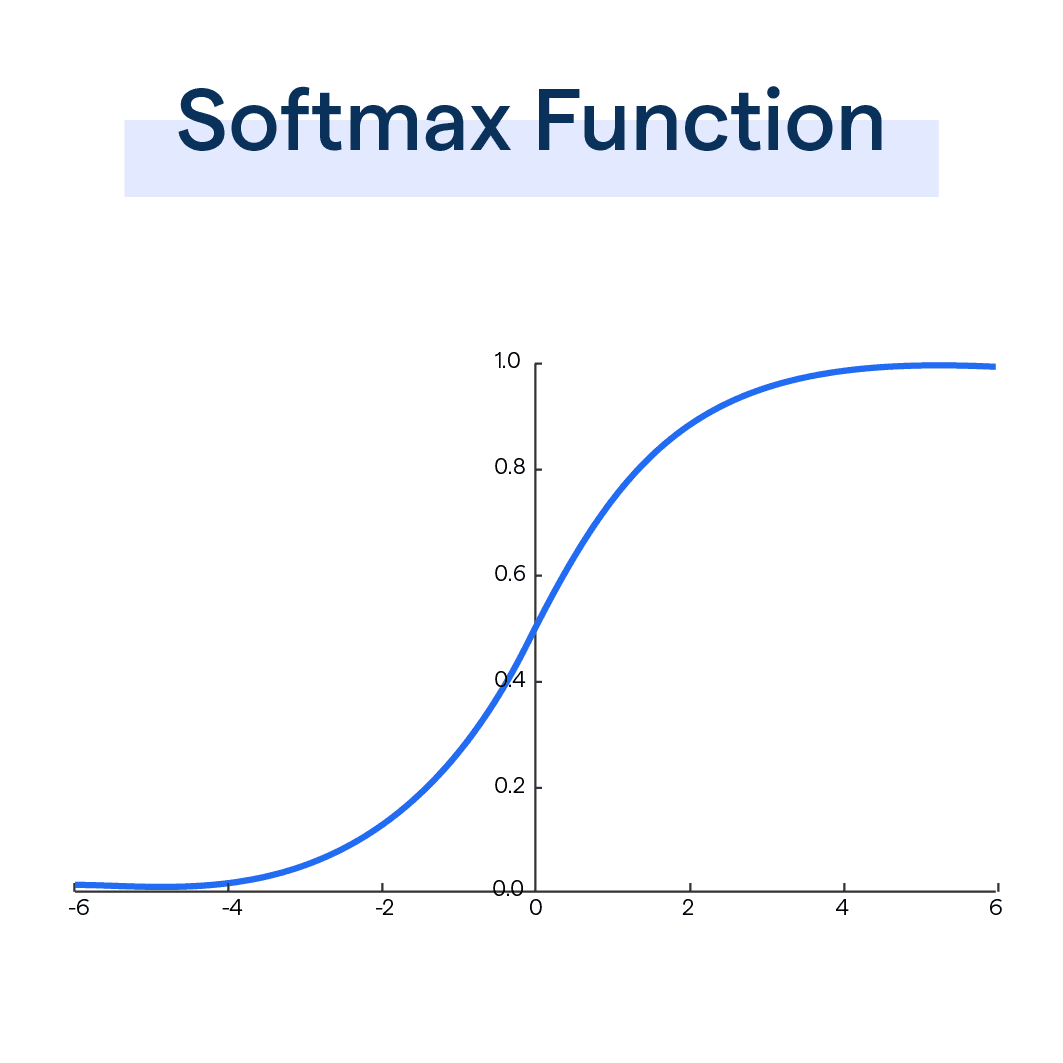
The Softmax Function is an activation function used in machine learning and deep learning, particularly in multi-class classification problems.
Its primary role is to transform a vector of arbitrary values into a vector of probabilities.
The sum of these probabilities is one, which makes it handy when the output needs to be a probability distribution.
Why is the Softmax Function Important?

Softmax comes into play in various machine learning tasks, particularly those involving multi-class classification.
It gives the probability distribution of multiple classes, making the decision-making process straightforward and effective.
By converting raw scores to probabilities, it not only provides a value to be worked with but also brings clarity to interpreting results.
Who can utilize the Softmax Function?
The Softmax Function is utilized by data scientists, machine learning engineers, and deep learning practitioners.
It's a fundamental tool in their toolkit, especially when they're working with models that predict the probability of multiple potential outcomes, as in the case of neural network classifiers.
When is the Softmax Function Used?
The Softmax Function comes into its own when dealing with multi-class classification tasks in machine learning. In these scenarios, you need your model to predict one out of several possible outcomes.
Softmax is typically applied in the final layer of a neural network during the training phase, converting raw output scores from previous layers into probabilities that sum up to one.
Where is the Softmax Function Implemented?
In practice, the Softmax Function finds its application in various fields where machine or deep learning models are used for prediction.
This could be anything from identifying objects in an image, predicting sentiment in a block of text, or even predicting market trends in finance.
Any field requiring a definitive class prediction based on multiple potential outcomes could benefit from the Softmax Function.
How does the Softmax Function work?
The Softmax function is a wonderful tool used predominantly in the field of machine learning and deep learning for converting a vector of numbers into a vector of probabilities.
But how does it do this? Let's break down its magic.
The Basic Calculation
The function works by taking an input vector and computing the exponential (e-power) of every number in the vector.
It then takes each of these results and divides each by the sum of the exponentials of all the numbers. This is the basic formula:
softmax(x)_i = exp(x_i) / Σ_j exp(x_j)
Here, x is the input vector, and i and j are individual indices in the vector.
Probabilistic Representation
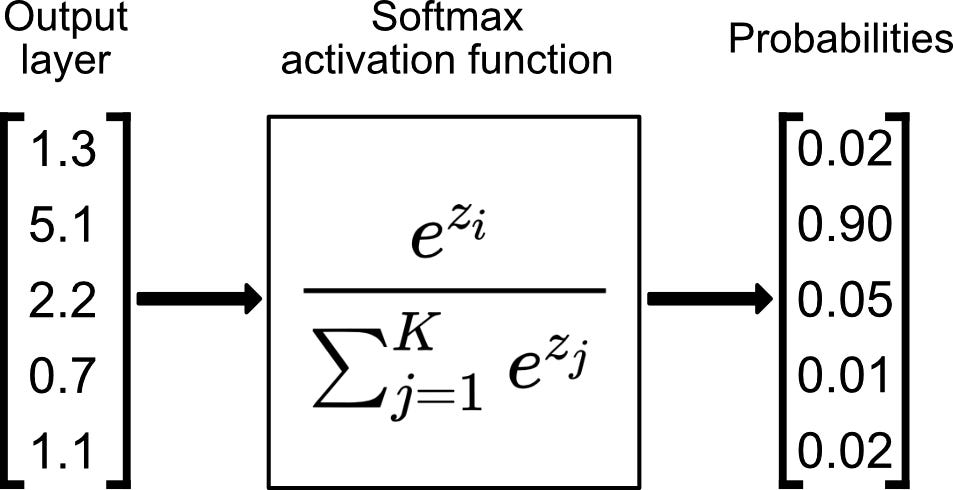
The output from this process is another vector, but with a twist - each element in the output vector represents the probabilistic representation of the input.
The values of the output vector are in the range of 0 to 1, and the total sum of the elements will be 1.
The Benefit of Softmax
The key advantage of the Softmax function is that it highlights the largest values and suppresses values which are significantly below the maximum value.
This behavior is very useful in multiclass classification problems where the model needs to be confident in its predictions, hence the extensive use of the Softmax function in deep learning for normalizing the output layer.
In Action: Classification
In the case of classification models, softmax is applied to the output layer of the model, which will then return the probabilities of each class.
The class with the highest probability is considered the model’s output (i.e., its prediction).
In a nutshell, the Softmax function interprets every number in the input vector as a representation of a certain degree or intensity, and it normalizes these values to get a probability distribution - super helpful in classification problems!
Advantages of Softmax Function
In this section, we'll discuss the key benefits of using a Softmax function in machine learning and deep learning applications.
Probabilistic Interpretation
The Softmax function converts a vector of real numbers into a probability distribution, with each output value ranging from 0 to 1.
The resulting probabilities sum up to 1, which allows for a direct interpretation of the values as probabilities of particular outcomes or classes.
Suitability for Multi-Classification Problems
In machine learning, the Softmax function is widely used for multi-classification problems where an instance can belong to one of many possible classes.
It provides a way to allocate probabilities to each class, thus helping decide the most likely class for an input instance.
Works Well with Gradient Descent
The Softmax function is differentiable, meaning it can calculate the gradient of the input values.
Therefore, it can be used in conjunction with gradient-based optimization methods (such as Gradient Descent), which is essential for training deep learning models.
Stability in Numerical Computation
The Softmax function, combined with strategies like log-softmax and softmax with cross-entropy, increases numerical stability during computations, which is important in deep learning models where numerical calculations can span several orders of magnitude.
Enhances Model Generalization
Softmax encourages model to be confident about its most probable prediction, while simultaneously reducing confidence in incorrect predictions.
This helps enhance the generalization ability of the model, reducing the chances of overfitting.
Induces Real-World Decision Making
As Softmax outputs class probabilities, it provides a level of uncertainty about the model's predictions, which closely aligns with real-world scenarios.
This is particularly useful in decision-making applications where understanding the certainty of model predictions can be critical.
Applicability Across Various Networks
The Softmax function can work effectively across numerous network structures, including convolutional neural networks (CNNs) and recurrent neural networks (RNNs).
It's also a crucial component of architectures like transformers used in natural language processing (NLP).
Applications of Softmax Function
In this section, we'll dive into various ways in which the Softmax function is applied.
Multiclass Classification Problems
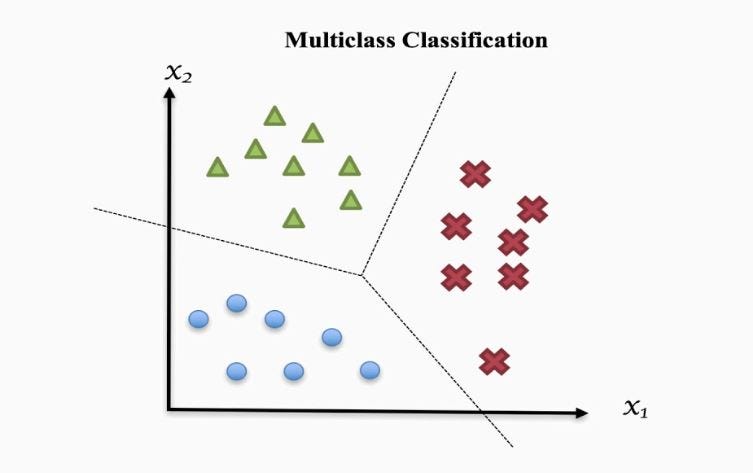
The Softmax function is extensively used in machine learning, particularly for multiclass classification problems.
It helps in assigning the probabilities to each class in a classification problem, ensuring that the sum of all probabilities equals one.
Probabilistic Models
Probabilistic models like the Gaussian Mixture model or soft clustering also apply the softmax function.
It helps in distributing probability mass among various components of the model.
Neural Networks
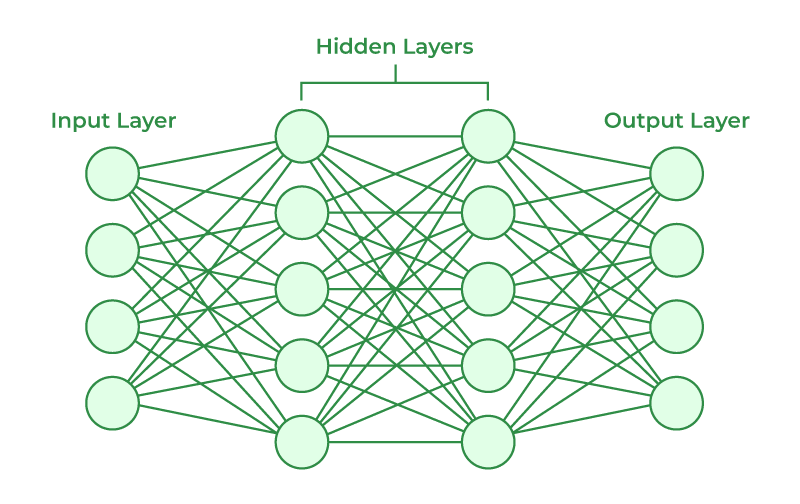
Neural Networks harness the Softmax function in the output layer. It translates the outputs of the network into probability values for each class in a multiclass problem, making the final decision of classification.
Deep Learning Models
Deep Learning models also apply the Softmax function in their architectures.
It's used in models for computer vision, natural language processing, and more, contributing to tasks such as object recognition, semantic segmentation, or machine translation.
Reinforcement Learning
In reinforcement learning, an agent can use the Softmax function to select an action to take in a particular state.
This helps in balancing exploration and exploitation, allowing the agent to learn and adapt effectively.
How to Implement the Softmax Function?
Implementing the softmax function is fairly straightforward if you're familiar with a programming language, especially one like Python, which is commonly used for mathematical operations and machine learning activities. Here's a quick guide:
Step 1
Import the Necessary Packages
First, import the required package. In Python, numpy is used for numerical computations.
import numpy as np
Step 2
Create the Softmax Function
Define the softmax function. The softmax function computes the exponential (e-power) of the given input value and the sum of exponential values of all the values in the inputs.
def softmax(inputs): return np.exp(inputs) / float(sum(np.exp(inputs)))
Step 3
Specify Your Inputs
You need to specify the input values to run the softmax function:
inputs = np.array([2.0, 1.0, 0.1])
Step 4
Run the Softmax Function
Finally, you can call the softmax function that you created with your specified inputs:
print("Softmax Function Output = ", softmax(inputs))
Once run, this program will apply the softmax function to the input array, and print out the results. It's worth noting that the results will all be probabilities and their sum will be approximately one.
That's it! The simplicity of implementation is one of the reasons the Softmax function is widely used across machine learning and data science fields.
Frequently Asked Questions (FAQs)
What is the Softmax Function used for in Machine Learning?
The Softmax Function is widely used in machine learning as it converts the output of a neural network into a probability distribution and enabling decision-making for classification tasks.
How does the Softmax Function avoid negative values in its calculation process?
The Softmax Function exponentiates the input array before division, which means that negative values are shifted towards zero, resulting in only non-negative outputs.
Is it possible to apply the Softmax Function to non-classification problems?
Yes, the Softmax Function can be used for any problem that requires calculation of a probability distribution from a set of numbers.
It is commonly used in multi-class classification but can also be used in other regression models.
How to select the number of neurons in the output layer when using the Softmax Function?
The number of neurons in the output layer of a model using the Softmax Function should match the number of classes in the classification problem.
For example, if there are five classes, five output neurons should be used.
What are the common techniques used to handle the overflow and underflow errors when calculating the Softmax Function?
To handle overflow and underflow errors, techniques such as the log-sum-exp trick, which works by using natural logarithms, can be implemented.
The max function can also be used to normalize the inputs before applying the exponential.