What is Combinatorial Optimization?
Combinatorial optimization is a fascinating area of study that focuses on finding the most optimal object from a finite set of possibilities.
With numerous applications in operations research, computer science, mathematics, and more, this field continues to grow and evolve, providing insights into various real-world problems. In this glossary, we delve deep into the key concepts and aspects of combinatorial optimization.
Algorithms
Algorithms lie at the heart of combinatorial optimization. These step-by-step procedures help find optimal solutions for complex problems.
Brute Force Algorithm
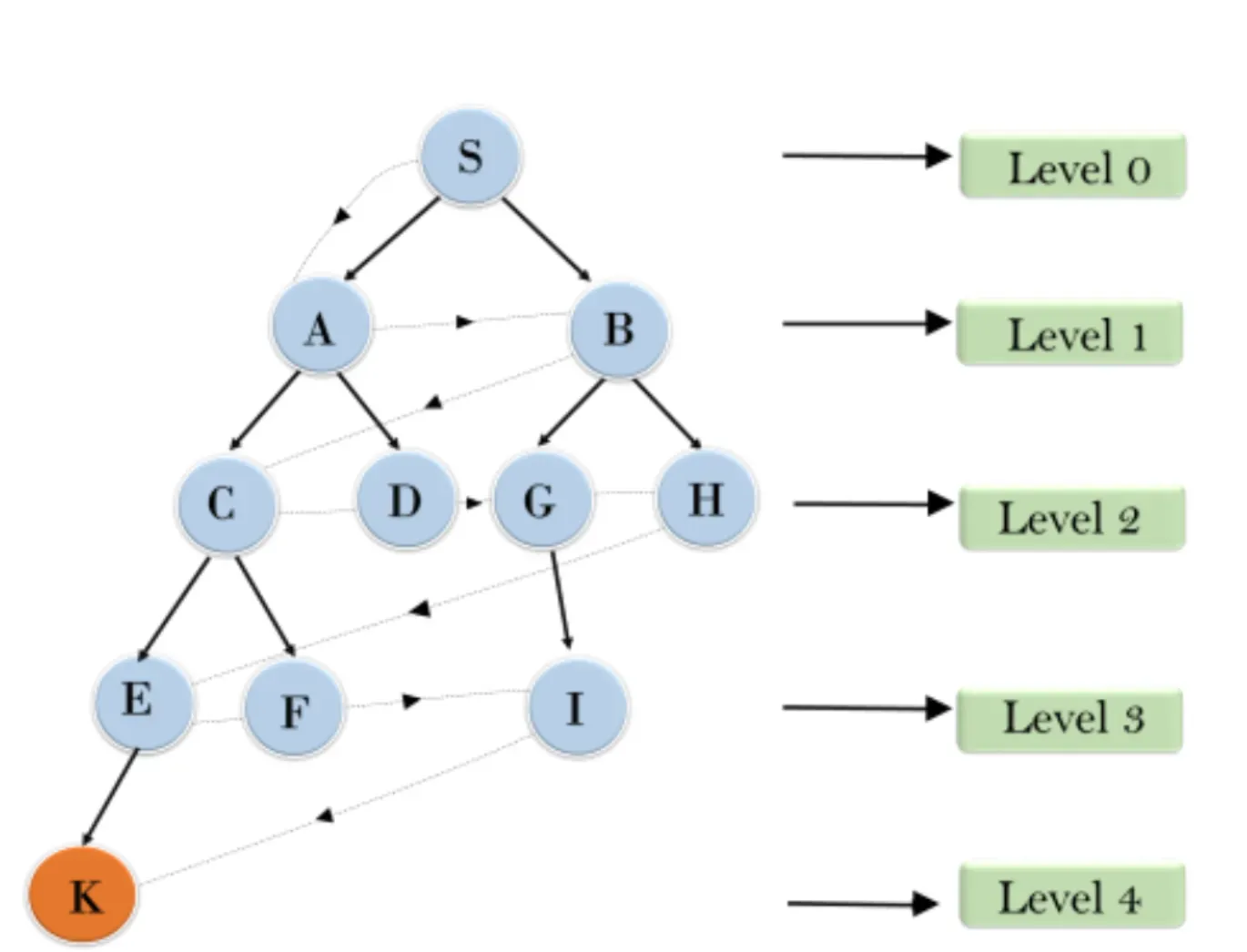
A brute force algorithm examines every possible solution for a problem in a systematic manner. While simple to implement, these algorithms tend to be inefficient for large problems, as their computational complexity can grow exponentially.
Greedy Algorithm
Greedy algorithms aim to find local solutions by making decisions that appear to be optimal at each step. While often easy to implement and fast to execute, greedy algorithms may not find the global optimum, especially in problems with a more complex structure.
Dynamic Programming
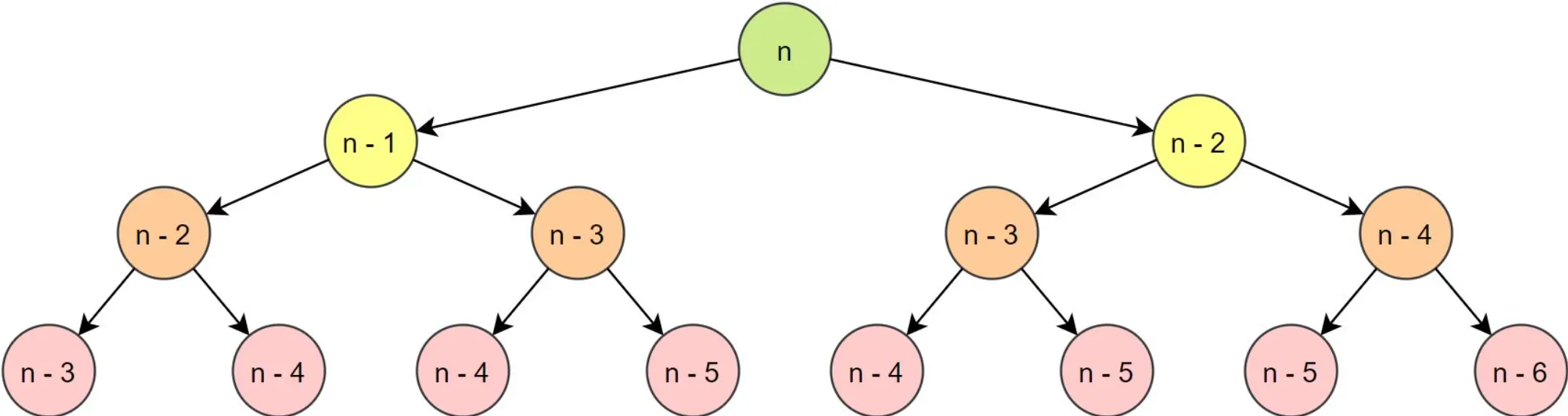
Dynamic programming is a technique that solves problems by breaking them down into smaller, overlapping subproblems. It then uses memoization to store and reuse previously computed solutions, making it an efficient approach for problems with overlapping substructures and optimal subproblem solutions.
Metaheuristic Algorithms
Metaheuristic algorithms are high-level problem-solving approaches that guide other algorithms to find near-optimal solutions. Examples include genetic algorithms, simulated annealing, tabu search, and ant colony optimization.
Branch and Bound
Branch and bound is an algorithmic framework that helps find optimal solutions for discrete and combinatorial optimization problems.
Branching
Branching is the process of dividing the problem into smaller subproblems by creating a decision tree. The tree's nodes represent possible decisions or constraints, while branches represent the connections between these nodes.
Bounding
Bounding involves setting upper and lower bounds for the optimal solution, enabling efficient pruning of insignificant branches and accelerating the solution search process. Bounding techniques can be problem-specific or general (e.g., linear programming relaxation).
Pruning
Pruning is the process of eliminating parts of the decision tree that are guaranteed not to contain the optimal solution based on the bounding information. Early pruning can significantly reduce the problem's search space, enhancing computational efficiency.
Backtracking
Backtracking is the process of returning to a previously explored decision node, undoing any decisions made at that level, and starting the search again. This strategy helps explore alternative paths in the search space that might lead to a better solution.
Complexity Theory

Complexity theory studies the inherent difficulty of computational problems and classifies them according to their computational resources, such as time and space.
Polynomial Time
A problem is solvable in polynomial time if there exists an algorithm that can find a solution within a number of steps that is proportional to a polynomial function of the input size (e.g., linear, quadratic, or cubic). Problems solvable in polynomial time are considered efficiently solvable.
NP-complete Problems
NP-complete problems are a distinct class of problems that are at least as hard as the hardest problems in NP (nondeterministic polynomial time). These problems are typically computationally intensive and lack efficient algorithms for finding optimal solutions.
Approximation Algorithms
Approximation algorithms aim to find near-optimal solutions to problems, with a guarantee on the solution's quality relative to the optimal one. These algorithms are particularly useful for tackling NP-hard problems, where finding an exact solution may be computationally infeasible.
Heuristics
Heuristics are problem-solving strategies that prioritize simplicity and practicality. They offer a fast, often efficient way to find good solutions but without any guarantee of optimality or approximation quality.
Decision Variables
Decision variables represent the choices made within combinatorial optimization problems.
Binary Decision Variables
Binary decision variables take on only two values: 0 or 1. They are especially useful for modeling problems that involve yes/no decisions or selecting from mutually exclusive options.
Integer Decision Variables
Integer decision variables are restricted to integer values, representing discrete quantities (e.g., the number of units produced or items selected).
Continuous Decision Variables
Continuous decision variables can take on fractional values within a specific range. They are more common in continuous optimization problems but can occasionally appear in combinatorial contexts (e.g., mixed-integer optimization).
Vector and Matrix Variables
Vector and matrix variables represent collections of decision variables. They are particularly useful for representing structured data, such as adjacency matrices in graph theory problems or assignment matrices in scheduling problems.
Frequently Asked Questions (FAQ)
What is the difference between combinatorial optimization and continuous optimization?
Combinatorial optimization focuses on problems with discrete or finite solution spaces, whereas continuous optimization deals with problems involving continuous variables and infinite solution spaces.
Why is combinatorial optimization important?
Combinatorial optimization helps solve complex real-world problems, such as scheduling, routing, and resource allocation. Its techniques and algorithms play a crucial role in decision-making and optimization across various domains.
What are some common application areas of combinatorial optimization?
Some common application areas include logistics, network design, manufacturing, project management, finance, and operations research.
Can all combinatorial optimization problems be solved efficiently?
Not all combinatorial optimization problems can be solved efficiently. Many problems, such as the traveling salesman problem (TSP), are NP-hard, making it challenging to find exact solutions in a reasonable amount of time.
What is the role of heuristics and metaheuristics in combinatorial optimization?
Heuristics and metaheuristics provide practical and efficient problem-solving strategies for complex problems, especially when exact solutions are computationally costly or infeasible. They help find good solutions quickly, even if they may not guarantee optimality.