Introduction to Dynamic Programming
Dynamic Programming sounds fancy, doesn't it? But it's not as complicated as it sounds. Imagine it as a method to solve problems by breaking them down into simpler subproblems. Let's dive into what exactly this approach is all about.
What is Dynamic Programming
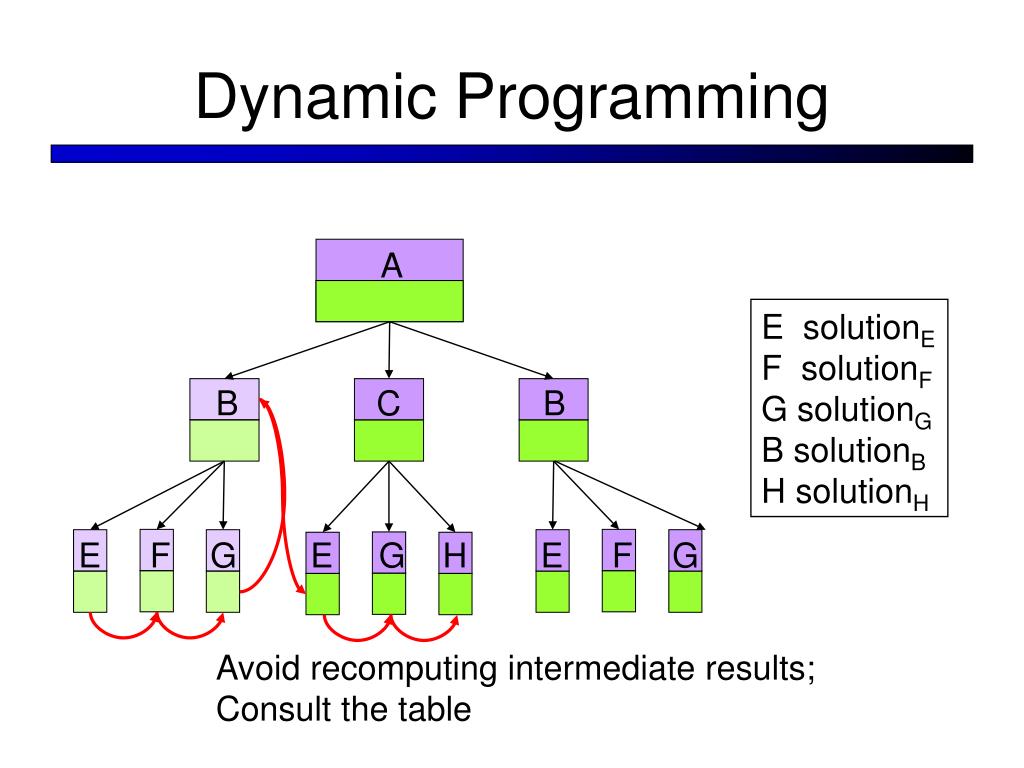
Dynamic Programming is like a strategy game where you solve complex problems by breaking them into smaller, more manageable chunks. Each chunk, or subproblem, is solved just once, and its solution is stored. This way, when you encounter that subproblem again, you don't waste time-solving it anew. Instead, you just fetch the solution you've already computed. It's like having a cheat sheet for tough problems!
Importance and Applications of Dynamic Programming

Dynamic Programming isn't just a fancy trick; it's a powerful tool used in various fields. Let's explore why it's so important and where it's applied.
Importance
Dynamic Programming is like having a superpower in problem-solving. It helps you tackle problems efficiently by avoiding redundant computations. Imagine you're trying to find the shortest path in a maze. Instead of trying every possible route from scratch each time, Dynamic Programming remembers the shortest path from each cell. So, when you reach a cell, you've been to before, you know the shortest path from there. It's like leaving breadcrumbs to find your way back!
Applications
Dynamic Programming is everywhere once you know where to look. From computer algorithms to everyday life problems, its applications are vast.
In computer science, dynamic programming is the backbone of many algorithms, such as the famous Fibonacci sequence and shortest path algorithms. It's like having a secret weapon in your coding arsenal.
In economics and finance, dynamic programming helps in decision-making in uncertain times. Think of it like a financial advisor predicting the best investment strategy for maximum profit with minimal risk.
In biology, dynamic programming is used in sequence alignment, which helps compare DNA or protein sequences efficiently. It's like solving a puzzle to understand the building blocks of life.
In Operations Research, Dynamic Programming optimizes resource allocation and scheduling. It's like finding the best route for a delivery truck to save time and fuel.
In Game Theory, Dynamic Programming models strategic decision-making in competitive situations. It's like playing chess, thinking ahead to outsmart your opponent.
Suggested reading: Application Programming Interface
Key Algorithms in Dynamic Programming

Dynamic Programming is like a treasure trove of clever algorithms that can solve a wide range of problems efficiently. Let's take a peek at some of the most popular ones.
Fibonacci Sequence: Imagine a sequence where each number is the sum of the two preceding ones (starting with 0 and 1). This seemingly innocent sequence is the basis for one of the most famous Dynamic Programming algorithms. It's like unraveling a mystery to find the next number in the sequence.
Knapsack Problem: Picture yourself with a knapsack, trying to maximize the value of items you can carry without exceeding its weight limit. This classic optimization problem is where Dynamic Programming shines. It's like packing for a trip, trying to fit in as much as possible without overloading yourself.
Longest Common Subsequence: Think of two sequences of items, and you want to find the longest sequence of items present in both, but not necessarily in the same order. Dynamic programming comes to the rescue here by efficiently finding the longest common subsequence. It's like spotting patterns in a jumble of words to find the hidden connection.
Suggested reading: Dynamic Link
How Does Dynamic Programming Work?
Dynamic Programming may sound complex, but it's actually pretty straightforward. Let's break down how it works into simple steps.
Steps in Formulating a Dynamic Programming Solution
Here's a quick guide on how to tackle a problem using Dynamic Programming:
Identify Subproblems: Start by breaking down the main problem into smaller, more manageable subproblems. These subproblems should be similar in nature and can often be solved independently.
Find Optimal Solutions: For each subproblem, find the optimal solution. This might involve solving the subproblems recursively or iteratively.
Store Solutions: Once you find the solutions to the subproblems, store them in a data structure. This prevents redundant computations and speeds up the overall process.
Construct Final Solution: Finally, use the solutions to the subproblems to construct the solution to the main problem. This might involve combining the solutions in a certain way to achieve the desired result.
Key Components
To implement a Dynamic Programming solution effectively, you need to understand its key components:
Recurrence Relations: These are mathematical equations that define the relationship between the solution to a larger problem and the solutions to its subproblems.
Memoization: This technique involves storing the results of expensive function calls and returning the cached result when the same inputs occur again.
Tabulation: Tabulation is an alternative approach to memoization where solutions to subproblems are stored in a table and filled iteratively.
Examples of Dynamic Programming Solutions
Let's explore some Dynamic Programming examples in action:
Fibonacci Sequence: This dynamic programming examples can efficiently calculate Fibonacci numbers by storing previously computed values and reusing them to compute new ones.
Knapsack Problem: When faced with the Knapsack Problem, Dynamic Programming can determine the optimal combination of items to maximize value without exceeding the weight limit.
Longest Common Subsequence: This Dynamic Programming examples shines in finding the longest common subsequence between two sequences of characters, efficiently identifying shared patterns.
suggested Reading: Dynamic Modelsdynami
Frequently Asked Questions(FAQs)
What is dynamic programming?
Dynamic programming is an optimization approach that solves complex problems by breaking them down into simpler subproblems, solving each once, and storing their solutions.
How does dynamic programming differ from recursion?
Dynamic programming uses memoization or tabulation to store the results of subproblems, thus avoiding the repeated work that pure recursion involves, which does not store solutions.
What are memoization and tabulation in dynamic programming?
Memoization and tabulation are techniques used in dynamic programming to store the results of subproblems. Memoization stores results on demand, while tabulation does it in a bottom-up manner.
When should I use dynamic programming?
Use dynamic programming when the problem can be broken down into overlapping subproblems whose solutions can be combined to solve the overall problem and when it has an optimal substructure.
Can dynamic programming be used for non-numeric problems?
Yes, dynamic programming can be applied to a wide range of problems, including non-numeric ones, as long as they can be broken into overlapping subproblems with optimal substructures
What are some common problems solved using dynamic programming?
Common problems solved using dynamic programming examples include Fibonacci sequence calculation, shortest path problems, knapsack problems, and edit distance problems. Dynamic programming offers efficient solutions to these and many other computational problems.
