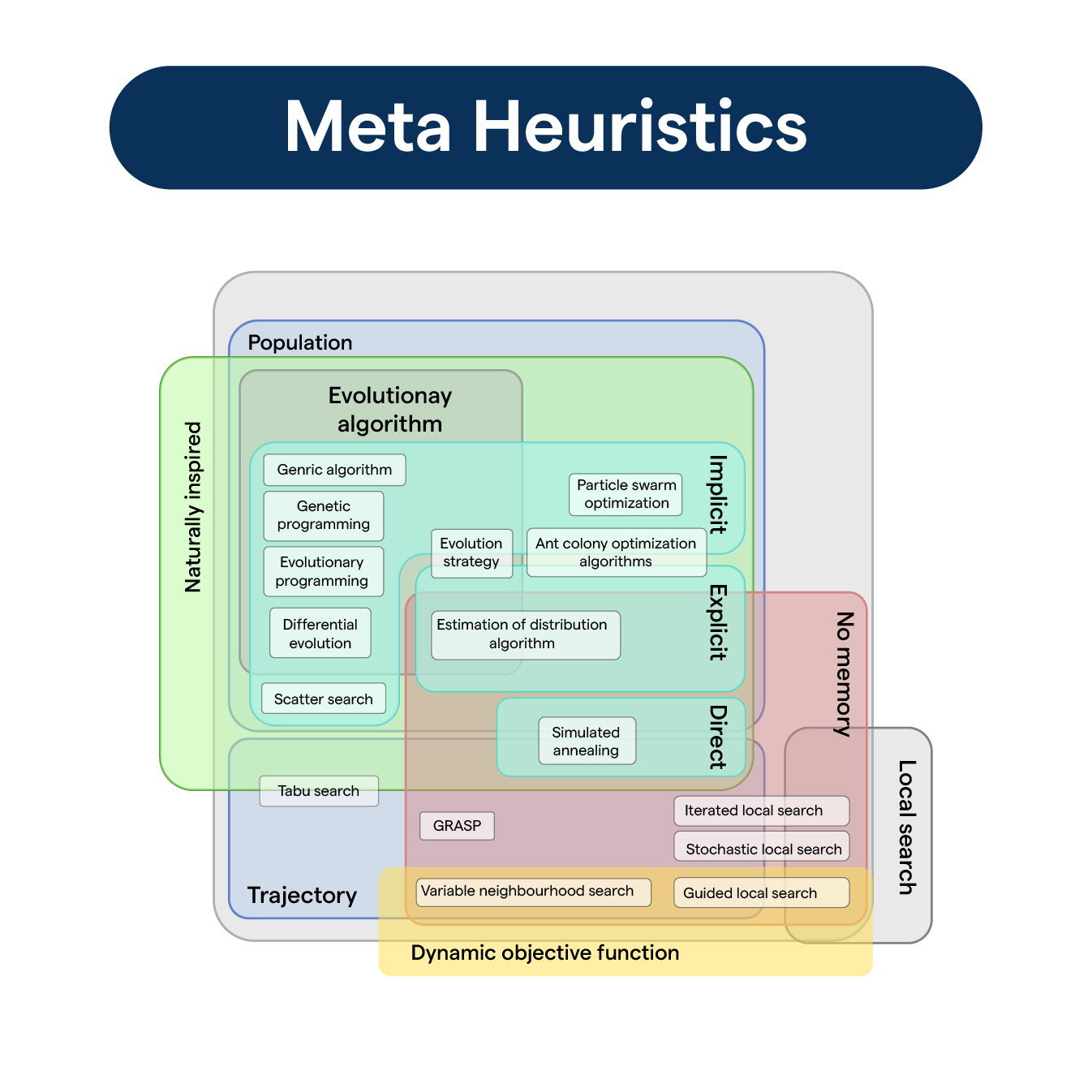
What are Metaheuristics?
Metaheuristics are strategies that guide the process of solving complex optimization problems that are hard to solve through traditional methods.
Key Characteristics
They are known for being flexible, adaptable, and capable of finding good enough solutions in a reasonable amount of time for very hard problems.
Applications
Useful in various domains like logistics, scheduling, network design, and many more, wherever complex optimization is needed.
Advantages
The beauty of metaheuristics lies in their applicability to a wide range of problems and the balance they maintain between exploration and exploitation.
Limitations
They don’t guarantee an optimal solution but are prized for their ability to find very good solutions more often than not.
Who Uses Metaheuristics?
Understanding who benefits from these nifty algorithms can shed light on their importance.
Computer Scientists
They often design and test metaheuristics to solve computational problems.
Operations Researchers
Professionals in this domain apply metaheuristics to optimize logistical operations.
Engineers
From designing efficient systems to optimizing resource use, engineers rely on metaheuristics for many solutions.
Economists
Economists use them for modeling and solving economic forecasting problems.
Data Scientists
They employ metaheuristics for optimizing machine learning models and dealing with big data challenges.
Why are Metaheuristics Used?
The reasons for choosing metaheuristics over other methods are quite intriguing.
Complexity Handling
For problems too complex for exact methods, metaheuristics offer a viable solution path.
Flexibility
They can be adapted to various types of problems without needing specific problem-domain knowledge.
Efficiency
Metaheuristics can find good solutions faster than exhaustive search methods, especially in large search spaces.
Scalability
They scale well with problem size, maintaining their ability to find good solutions even as the problem grows.
Accessibility
The general principles of metaheuristics can be understood and applied without in-depth knowledge of the problem domain.
When are Metaheuristics Used?
Timing can be everything when it comes to employing metaheuristics.
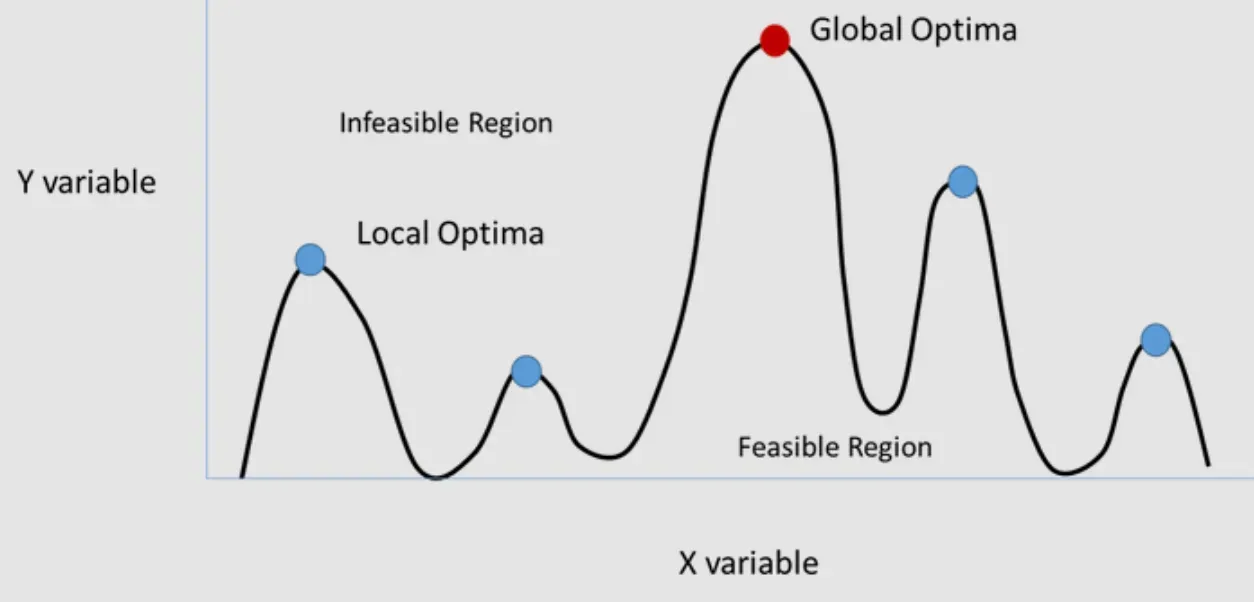
Solving NP-Hard Problems
When problems are NP-Hard, meaning no known algorithm can solve them quickly as the problem size increases, metaheuristics come to the rescue.
Limited Computation Time
When quick decisions are needed, and there’s not enough time for exhaustive searches.
New Problem Domains
In newer or less studied problem areas where bespoke solutions haven’t been developed.
High Dimensionality
For problems with many variables (high dimensionality), where traditional methods struggle.
Real-World Applications
Whenever real-world complexity renders traditional optimization methods inadequate or infeasible.
How Are Metaheuristics Implemented?
Let’s walk through the nuts and bolts of how metaheuristics are brought to life.
Algorithm Selection
Choosing the metaheuristic algorithm best suited for the problem at hand, such as genetic algorithms, simulated annealing, or others.
Parameter Setting
Fine-tuning parameters that control the algorithm's behavior, which can significantly influence the solution quality.
Problem Encoding
Designing a way to represent the problem so that the metaheuristic algorithm can work on it effectively.
Solution Evaluation
Creating a mechanism to evaluate how good a solution is relative to others, usually through a fitness function or objective function.
Iterative Improvement
Running the algorithm, which iteratively searches for better solutions until a stopping condition is met (like time limit or solution quality).
Key Components in Metaheuristics
Understanding the building blocks can make metaheuristics less of a black box.
Exploration and Exploitation
Balancing the search between exploring new areas and exploiting known good areas is critical for effectiveness.
Fitness Function
This evaluates how close a given solution is to the optimum, guiding the search process.
Operators
Actions that modify solutions, such as mutation in genetic algorithms, are tailor-made to navigate the solution space.
Population
Some metaheuristics work with a single solution at a time, while others like genetic algorithms evolve a set of solutions.
Termination Criteria
Determines when the algorithm should stop, often a function of time, iterations, or lack of improvement.
Types of Metaheuristics
Diving deeper, let’s look at some commonly used metaheuristic algorithms.
Genetic Algorithms
Inspired by the process of natural selection, these algorithms evolve solutions over time.
Simulated Annealing
Mimics the process of heating and slowly cooling metal to minimize energy states, used analogously to find minimum cost solutions.
Ant Colony Optimization
Draws inspiration from the foraging behavior of ants and their ability to find shortest paths.
Particle Swarm Optimization
Imitates the social behavior of animals (like birds flocking) to explore the solution space.
Tabu Search
Employs a memory structure to store previously visited solutions to avoid cycling back to them.
Challenges in Metaheuristics
Despite their versatility, metaheuristics face challenges that affect their effectiveness.
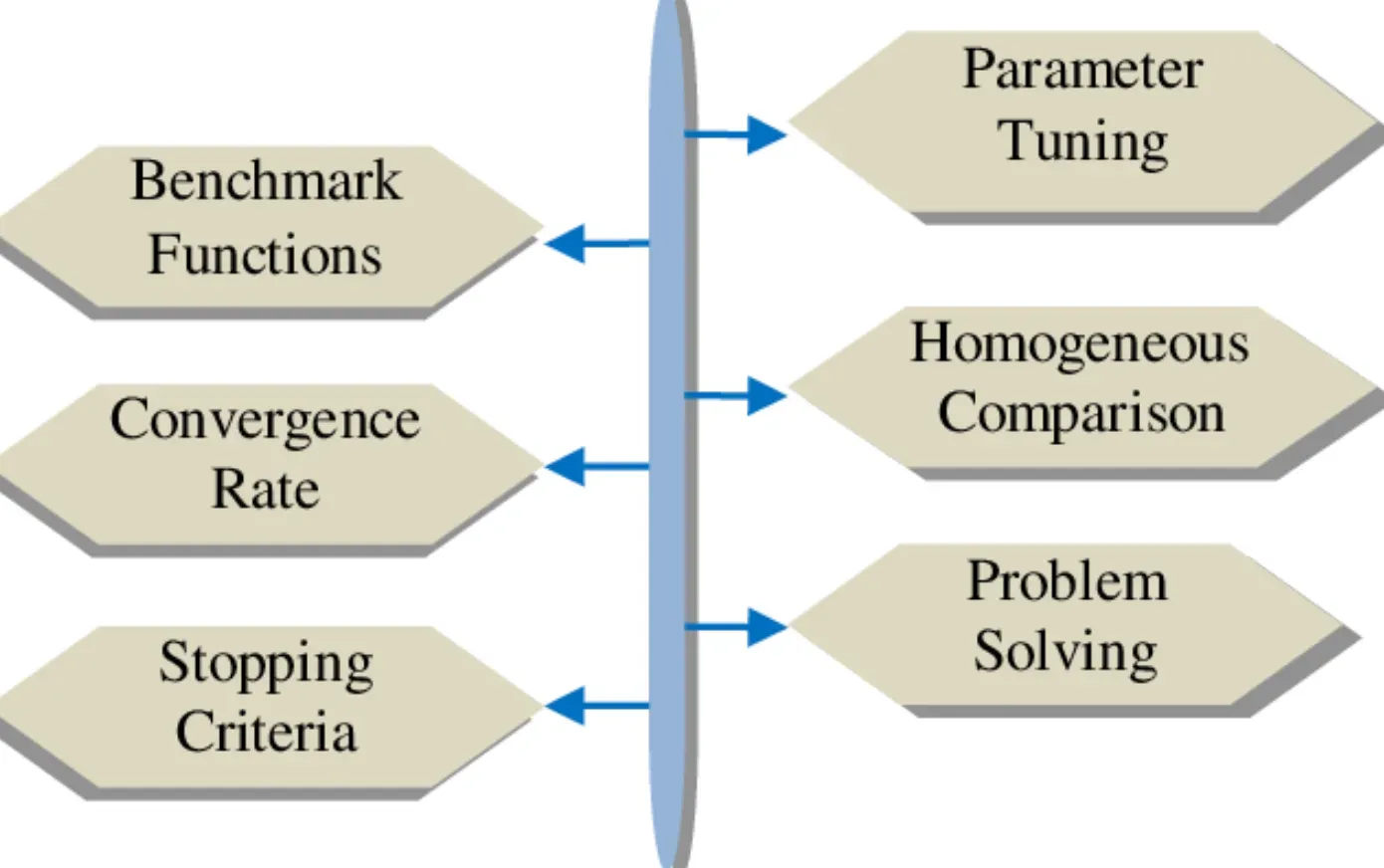
Parameter Tuning
Finding the optimal set of parameters for an algorithm can be time-consuming and requires expertise.
Convergence
Ensuring the algorithm converges to a good solution without getting stuck in local optima is challenging.
Scalability
Maintaining effectiveness as problem size and complexity increase is an ongoing challenge.
Theoretical Understanding
The lack of comprehensive theoretical frameworks for many metaheuristics can make their behavior difficult to predict.
Solution Quality
Balancing the solution quality with computational resources is a fine line that needs careful consideration.
Best Practices in Metaheuristics
Applying best practices can significantly improve the outcomes of metaheuristic applications.
Understand the Problem
A deep understanding of the problem and domain can guide the choice and customization of the algorithm.
Experimentation
Iterative testing and experimentation with different algorithms and parameters can yield better results.
Hybrid Approaches
Combining elements from different metaheuristics or incorporating problem-specific knowledge can enhance performance.
Use Existing Libraries
Leveraging existing software libraries can save time and provide insights into the algorithms’ inner workings.
Continuous Learning
Staying updated with the latest research and advancements in the field can reveal new and more effective strategies.
Trends in Metaheuristics
Emerging trends are shaping the future direction of metaheuristic research and applications.
Machine Learning Integration
Incorporating machine learning techniques for parameter tuning and strategy selection is growing in popularity.
Parallel and Distributed Computing
Utilizing powerful computing resources to run metaheuristic algorithms in parallel can drastically reduce computation times.
Real-World Applications
Expanding the use of metaheuristics to solve real-world problems across various domains continues to grow.
Adaptive Mechanisms
Developing algorithms that can adapt their strategies during the search process is an area of active research.
Green Computing
Efforts to increase the energy efficiency of metaheuristic algorithms are becoming more prominent.
Frequently Asked Questions (FAQs)
What are metaheuristics used for?
Metaheuristics are used to solve complex optimization problems where an exhaustive search isn't feasible due to the problem’s size, time constraints, or complexity.
How do metaheuristics differ from heuristics?
Unlike heuristics, which are problem-specific, metaheuristics are higher-level, generic strategies that guide the search process to efficiently explore the solution space.
Can metaheuristics guarantee optimal solutions?
Typically, metaheuristics cannot guarantee optimal solutions but are effective in finding good-quality solutions within reasonable computation times.
What are some examples of metaheuristics?
Well-known metaheuristics include Genetic Algorithms, Simulated Annealing, Tabu Search, and Ant Colony Optimization.
How does diversification and intensification play into metaheuristics?
Diversification refers to exploring the solution space broadly, while intensification focuses on searching around promising solutions. Balancing these is key to avoid being trapped in local optima.