What is Greedy Algorithm?
A Greedy Algorithm is a problem-solving approach that optimizes the solution by making the locally optimal choice at each step, hoping to find a global optimum solution.
In other words, a Greedy Algorithm always chooses the next best thing without worrying about the consequences in the future.
Problem-Solving Heuristic
Greedy algorithms are used to solve optimization problems that require finding the best possible solution.
These algorithms work by iteratively picking the best candidate from the available options and adding it to the solution set until the whole problem is solved.
Local optimization
The locally optimal choice at each step taken by a Greedy Algorithm may not always lead to a global optimal solution. But, it tries to find the best possible solution by making the most optimal decision at each step.
Components of Greedy Algorithms
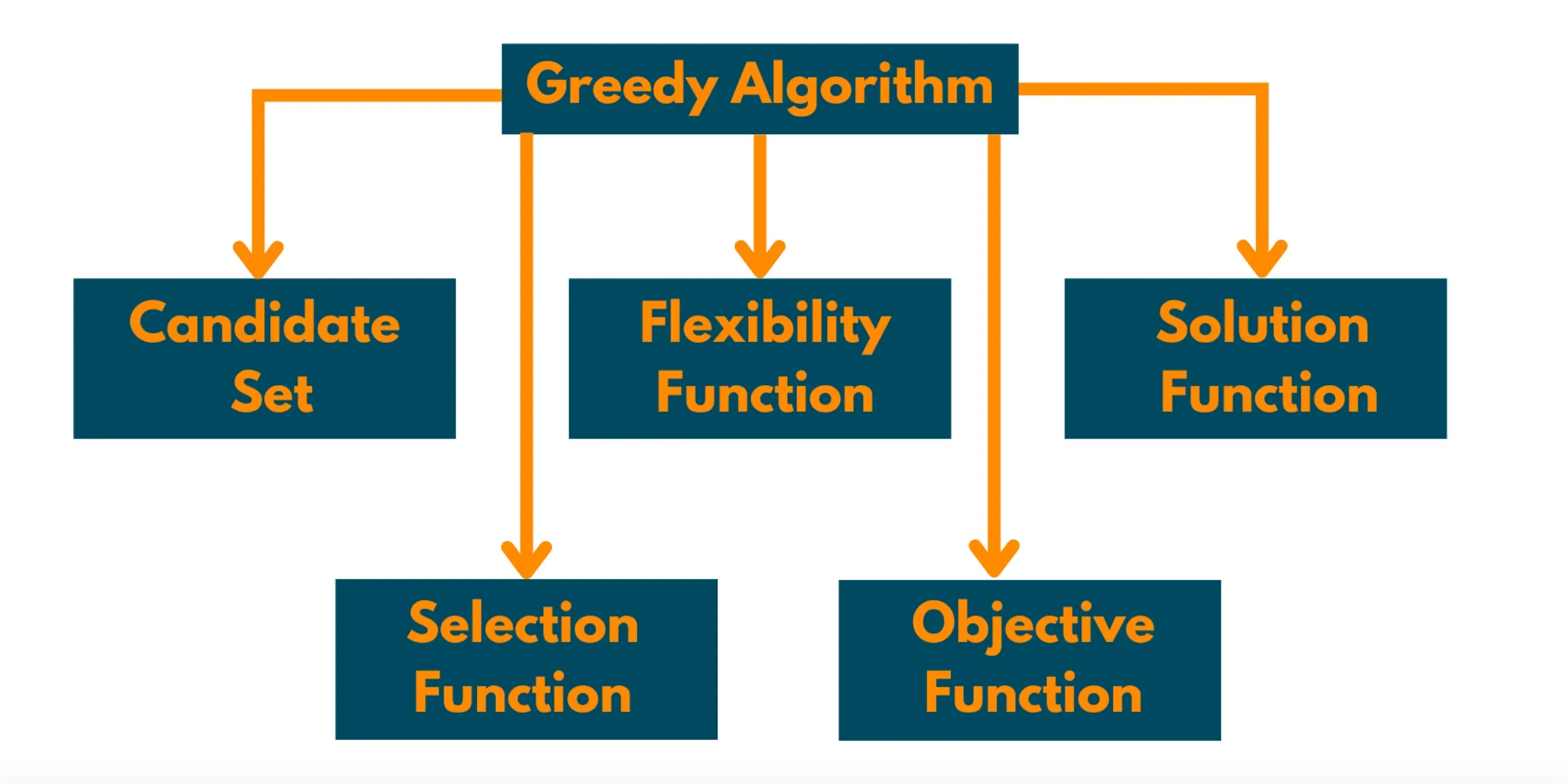
In the realm of Greedy Algorithms, key components shape the decision-making process: candidate set, selection, feasibility, objective, and solution functions. Let’s learn more about them.
- Candidate Set: The candidate set is the set of available choices or options that the Greedy Algorithm chooses from at each step. The Greedy Algorithm makes the locally optimal choice from this set.
- Selection Function: The selection function is a function that determines the criteria for selecting the next item from the candidate set that will be added to the solution.
- Feasibility Function : The feasibility function checks whether the selected item from the candidate set can be added to the current solution set or not.
- Objective Function: The objective function is used to evaluate the quality of the final solution produced by the Greedy Algorithm.
- Solution Function: The solution function takes the output of the Greedy Algorithm and converts it into the desired output format.
Properties of Problems Solved by Greedy Algorithms
Here are the properties of problems that are typically solved by Greedy Algorithms, along with brief explanations:
- Greedy Choice Property: The problem must exhibit the Greedy Choice Property, which means that at each step or subproblem, the local optimal choice leads to the globally optimal solution. This property ensures that the Greedy Algorithm consistently makes the best choice at each step.
- Optimal Substructure: The problem must have an optimal substructure, which means that an optimal solution to the problem contains optimal solutions to its subproblems.
This property allows the Greedy Algorithm to build up the overall optimal solution by consistently making locally optimal choices.
- No or limited backtracking: Greedy Algorithms typically make irreversible decisions, meaning there is no or limited backtracking.
Once a decision is made, it cannot be changed or reconsidered in future steps. This property simplifies the implementation and reduces the computational complexity.
- Independent subproblems: The subproblems of the problem being solved by the Greedy Algorithm should be independent. This means that solving one subproblem does not affect the solution or choices made for other subproblems. This property allows for a divide-and-conquer approach to solving the problem.
Characteristics of Greedy Algorithm
Here are the characteristics of a Greedy Algorithm with brief explanations:
- Ordered list of resources: Greedy Algorithms often work in conjunction with an ordered list of resources. The algorithm selects the best resource from the list in a particular order until a solution is found.
- Maximum resource approach: In the maximum resource approach, the Greedy Algorithm tries to maximize the resource, such as profit or efficiency, at each step.
This involves choosing the locally optimal solution that maximizes the amount of resources gained.
- Decision-making at each step: In a Greedy Algorithm, decisions are made at each step based on the current conditions of the problem.
The algorithm selects the best option available immediately without considering the consequences of future decisions.
- Well-defined subproblems: Greedy Algorithms work well in problems with well-defined subproblems. Each subproblem should be solvable independently, and the solution to the global problem should be obtained by combining the solutions of its subproblems.
- Efficient in time and space: The time and space complexity of Greedy Algorithms is usually more efficient than other optimization algorithms.
This makes them useful for solving large problems with limited computational resources.
Applications of Greedy Algorithm

- Activity Selection Problem: The activity selection problem is a famous application of a Greedy Algorithm. In this problem, a person has to choose the highest number of activities they can participate in, given a list of activities that have their start and end times.
- Fractional Knapsack problem: The Fractional Knapsack problem is another popular application of a Greedy Algorithm.
In this problem, we have to fill a knapsack with items of different weights and values, such that the total weight of the knapsack is less than or equal to a given limit.
- Job Sequencing: Job sequencing is a scheduling problem where given a set of jobs with their respective deadlines and profits, the objective is to find the maximum profit by scheduling the jobs in a way that maximizes the output.
- Huffman Coding: Huffman coding is a data compression technique that uses a Greedy Algorithm to assign variable-length codes to characters based on their frequency of occurrence.
- NP-Hard problems: Greedy Algorithms are also used in solving NP-hard problems, where finding the optimal solution is practically impossible. In such cases, Greedy Algorithms are used to find an approximate solution.
Advantages of Greedy Algorithms
The advantages of greedy algorithms are:
Easy Implementation
Greedy Algorithms are relatively easy to implement compared to other complex algorithms.
They often involve simple logic and straightforward steps, making them accessible for problem-solving.
Smaller Time Complexities
Greedy Algorithms tend to have smaller time complexity compared to other algorithms.
This means that they can execute faster, making them more efficient for solving problems, especially with limited computational resources.
Optimization and Approximate Solutions
Greedy Algorithms can be used to find optimal or approximate solutions for a wide range of problems.
While they may not always guarantee the absolute best solution, they can often provide a sufficiently good solution in a reasonable amount of time.
Flexibility and Adaptability
Greedy Algorithms can be adapted and modified to handle variations of a problem.
Their simple nature allows for easy tweaking and experimentation to find the best fit for a specific context or set of constraints.
Heuristics for Complex Problems
Greedy Algorithms can serve as heuristics for solving complex problems.
They can provide a useful starting point and guideline for finding solutions and can be combined with other algorithms or techniques to improve results.
Disadvantages of Greedy Algorithms
- Local Optima vs. Global Optima: Greedy Algorithms may sometimes get stuck in local optima and fail to reach the global optimum solution.
This happens when the algorithm makes locally optimal choices at each step, but these choices do not lead to the best overall solution.
- Limited Application: Greedy Algorithms have limited applicability as they can only be used to solve problems that satisfy the Greedy Choice Property and have optimal substructure, which are not very common in real-world scenarios.
- Lack of Flexibility: Greedy Algorithms are not very flexible in terms of adapting to changes in the problem or adding new constraints.
This is because the algorithm makes decisions based on the current state of the problem and does not take future changes or modifications into account.
- Not Always the Optimal Solution: Greedy Algorithms may not always lead to the optimal solution, even if they find a locally optimal solution.
This is because they rely on the greedy heuristic, which may not always make the best choice at each step.
- Difficult to Prove Optimality: Proving the optimality of a Greedy Algorithm for a given problem is often a difficult task. In some cases, the algorithm's optimality can only be proven under specific conditions or with specific constraints.
Frequently Asked Questions (FAQs)
What is Greedy Algorithm and can it be used for optimization problems?
A greedy algorithm is a problem-solving method that follows a simple, intuitive strategy: at each step, it chooses the most advantageous option available, without considering future implications.
This approach aims for local optimization, hoping it leads to a globally optimal solution, though it's not guaranteed for all problems.
Yes, Greedy Algorithms can be used for optimization problems where the objective is to maximize or minimize a certain value, such as maximizing profit or minimizing distance.
Are Greedy Algorithms always the best choice for solving optimization problems?
No, Greedy Algorithms are not always the best choice. While they can provide efficient solutions for some problems, they may not always produce the optimal solution or work for problems that do not meet the required properties.
Are Greedy Algorithms suitable for dynamic programming problems?
While Greedy Algorithms and dynamic programming share some similarities, they are different approaches. Greedy Algorithms make locally optimal choices at each step, while dynamic programming builds solutions by solving overlapping subproblems.
Can Greedy Algorithms be applied to graph problems?
Yes, Greedy Algorithms can be applied to graph problems. For example, Dijkstra's algorithm and Prim's algorithm are both examples of Greedy Algorithms used to solve graph-related problems.
How do you analyze the time complexity of a Greedy Algorithm?
The time complexity of a Greedy Algorithm depends on the specific problem and its implementation. It typically involves iterating through the list of resources or steps, resulting in a time complexity of O(n) or O(log n), where n is the size of the input.


