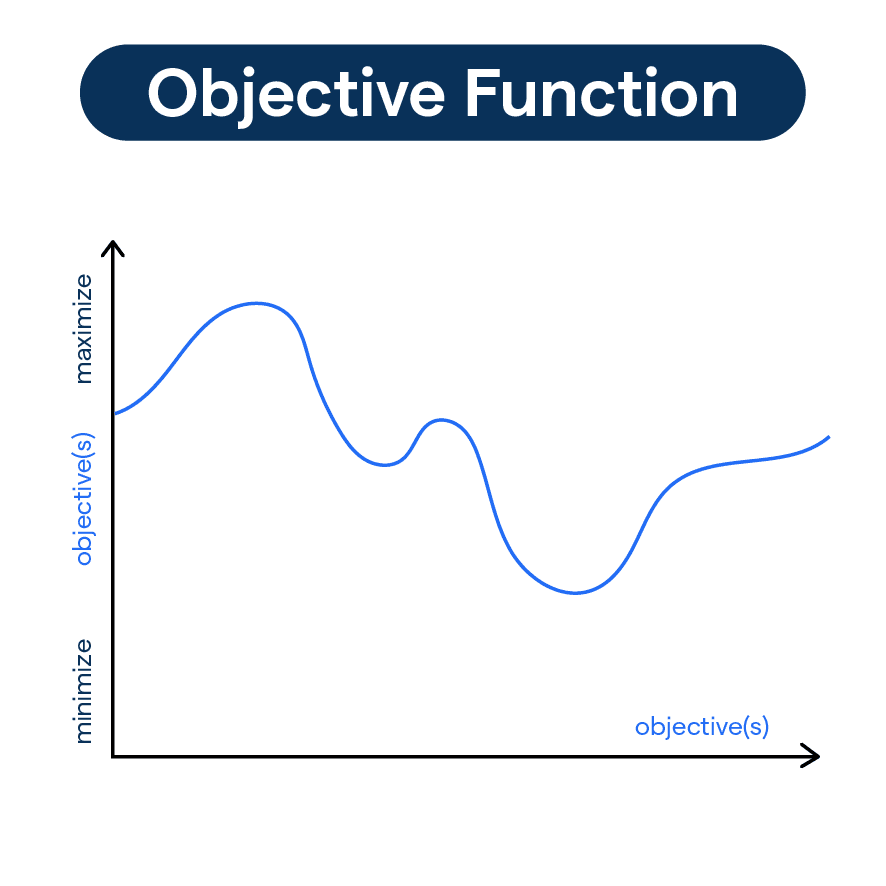
What is an Objective Function?
At its core, an objective function is a mathematical representation of our desired outcome. It enables us to measure the success of our solution by assigning a numerical value to it.
In linear programming, the objective function is typically expressed as a linear equation, combining decision variables and their coefficients.
Why is the Objective Function Important?
The objective function holds tremendous importance in the world of optimization. It allows us to define and prioritize our objectives, guiding us towards optimal decisions.
By systematically quantifying these objectives, we can effectively evaluate different courses of action and select the one that best meets our goals.
When is the Objective Function Used?
The objective function is used whenever there is a need to make optimal decisions within a set of constraints.
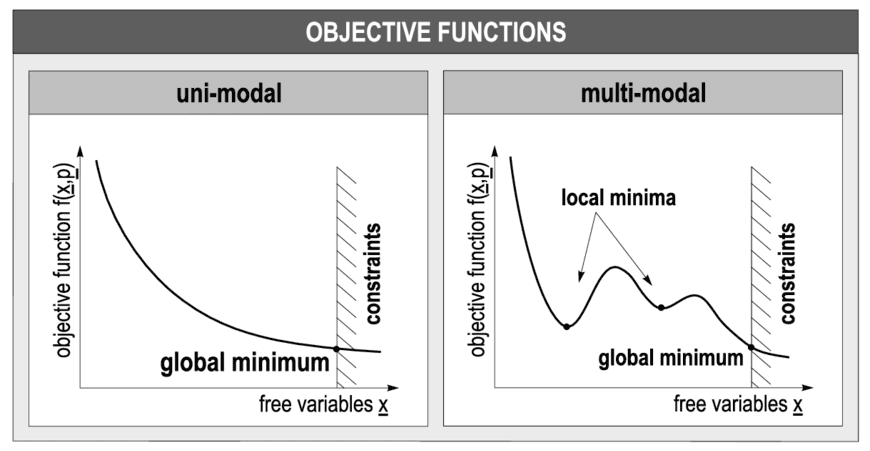
It finds applications in various industries, such as supply chain management, manufacturing, finance, transportation, and more. Whenever we encounter a problem where we need to optimize our resources, the objective function comes into play.
Where is the Objective Function Used?
The objective function finds utility in a wide range of domains. In industries like oil and chemical refining, it helps optimize production processes and maximize profitability.
In vendor selection scenarios, it assists in identifying the most cost-effective suppliers. It aids in determining the optimal shipping routes in logistics and optimizing fleet management for transportation companies.
How to Solve an Objective Function?
An objective function is a mathematical expression that needs to be maximized or minimized. The goal is to find the best solution for a particular problem within given constraints.
Identifying the Variables
Define the variables utilized in the objective function. These will change and adapt until the optimal condition is found.
Setting up Constraints
Constraints are often a set of inequalities or equalities involving the variables. It is within these constraints that the objective function must find its optimal value.
Visualizing the Feasible Region
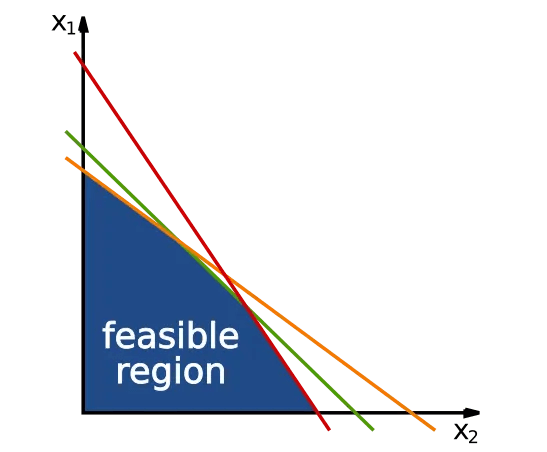
Graphically representing the constraints helps in identifying the feasible region: the set of all possible solutions to the given constraints. In high-dimensional cases, computational methods might be needed.
Finding Optimal Solution
For linear functions, the optimal solution is always at the vertices or corners of the feasible region. By substituting the coordinates of these vertices back into the objective function, the values can be compared to identify the optimal solution.
Verifying the Solution
Once identified, double-check the solution for feasibility. The result should satisfy all the initial constraints and should also verify if the objective function has been minimized or maximized (as originally intended).
The process of solving an objective function involves a combination of variable identification, constraint application, solution visualization, rigorous analysis, and final solution verification, ensuring that the best possible result is achieved.
How to Maximize an Objective Function?
This section will help you in understanding the steps and methods involved in optimizing an equation for the maximum output value.
Identifying the Objective Function
The first step in maximizing an objective function is correctly identifying it.
This function represents an equation that you wish to optimize - it could represent maximizing profits, improving efficiency, or increasing production levels in a real-world setting.
Understanding the Constraints
The constraints are a key component of the problem. They represent certain conditions or limitations that the solutions must adhere to.
Identifying these restrictions helps narrow down the feasible solutions. For example, budget limited might be a constraint when maximizing a company's profits.
Leveraging Graphical Analysis
When dealing with problems involving two variables, using graphical analysis can often simplify the task.
By graphing the constraints and determining the feasible region (the area that satisfies all the constraints), one can visually inspect possible solutions.
Finding Feasible Solutions
Feasible solutions denote a set of values that satisfy all the given constraints.
Depending on the complexity of the problem, you can use algebraic methods, quadratic programming, linear programming, or other optimization techniques to find these solutions.
Determining the Optimal Solution
Once you have the feasible solutions, the next step is to determine which of them, when substituted into the objective function, will produce the maximum output.
This solution is the 'maximum' or the optimal solution.
How to Minimize an Objective Function?
In this section, we will discuss ways to minimize an objective function, a crucial step in a variety of computational problems ranging from business optimization to machine learning models.
Understanding the Objective Function
An objective function, also known as a cost or a loss function, measures the difference between the prediction from a model and the actual outcome, with the aim being to minimize this difference.
It quantifies the goal of a computational problem, acting as a guide for decision-making processes.
Simply put, the objective function defines what we're trying to minimize.
Selection of Optimization Algorithm
To minimize an objective function, an optimization algorithm must be selected. This algorithm helps find the minimum value of the objective function.
The choice of the optimization algorithm can depend on several factors, like the nature of the problem, computational expense, precision required, and more.
Commonly used optimization algorithms include Gradient Descent, Stochastic Gradient Descent, Newton's Method, and more.
Initializing Parameters
The parameters of your algorithm need to be initialized. These initial parameter settings affect the starting point of the optimization process.
It's essential to choose an appropriate initialization method, as a poor choice can lead to slow convergence or the algorithm getting trapped at inferior local minima.
Iterative Processing
Optimization is an iterative process. Each iteration involves calculating the value of the objective function and adjusting the parameters, aiming to reduce the function's value.
The adjustments are typically based on the gradients (derivative) of the objective function with respect to each parameter.
Regularization and Checking Convergence
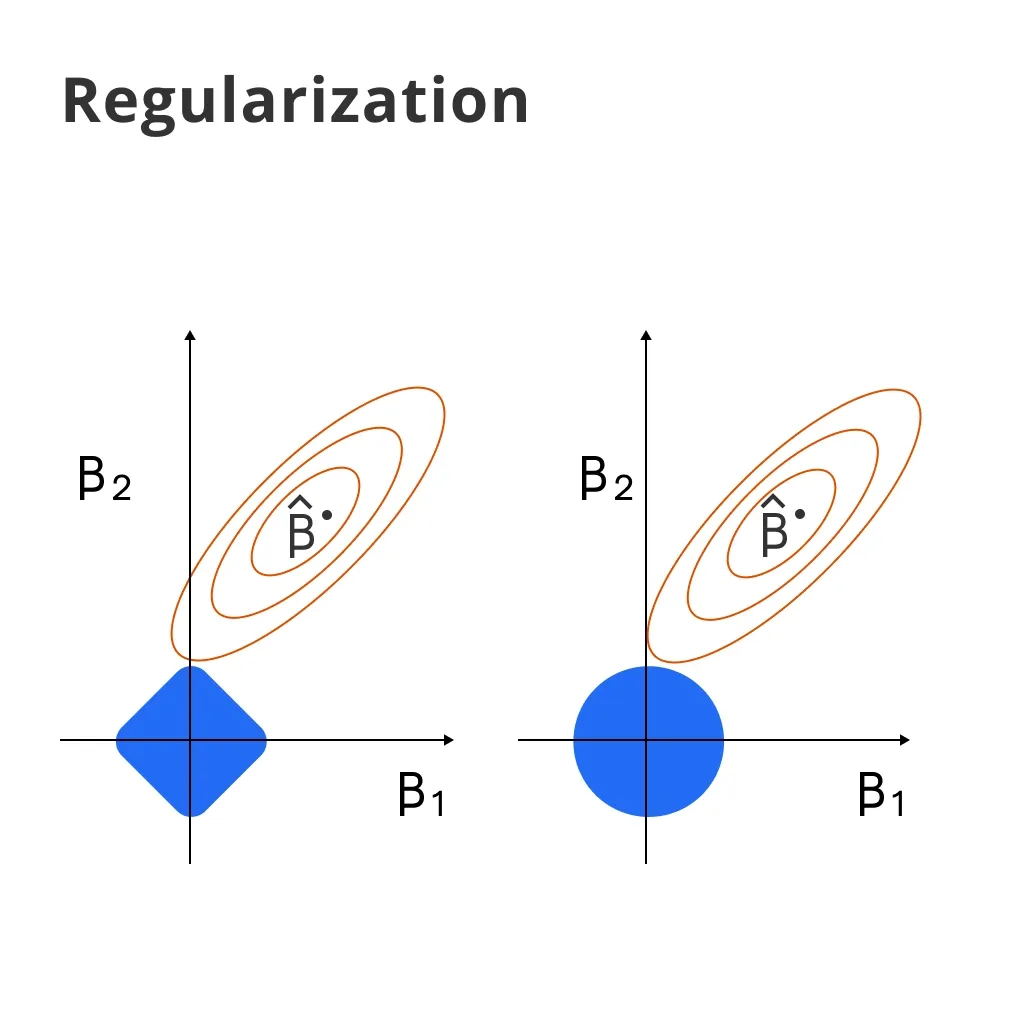
Regularization techniques, like L1 and L2 regularization, can help prevent overfitting by adding a penalizing term to the objective function.
Moreover, it's also important to monitor the convergence of your optimization algorithm.
Convergence is when the values of the parameters and objective function stop changing significantly, indicating the minimal point might have been reached.
Frequently Asked Questions (FAQs)
What is Objective Function and its Purpose?
An objective function is a mathematical function that an algorithm tries to optimize.
In machine learning, it's the function that the algorithm tries to minimize (like error) or maximize (like accuracy) during training.
Its purpose is to quantify our goals and objectives mathematically, helping us make better decisions and find optimal solutions in various fields.
How is the objective function used in optimization?
The objective function is used to measure the success of our solution by assigning a numerical value to it.
It helps us prioritize objectives and select the best course of action.
Can you give examples of industries where objective functions are used?
Objective functions are used in industries like supply chain management, manufacturing, finance, transportation, oil and chemical refining, and more, to optimize processes and maximize profitability.
What are the steps to solve an objective function?
The steps to solve an objective function include formulating the objective, defining constraints, graphically representing the feasible region, determining the optimal solution, and conducting sensitivity analysis.
What are the types of objective functions?
There are maximization objective functions, used to maximize the value of the objective, and minimization objective functions, used to minimize the value.
They can also be standard or have mixed constraints.