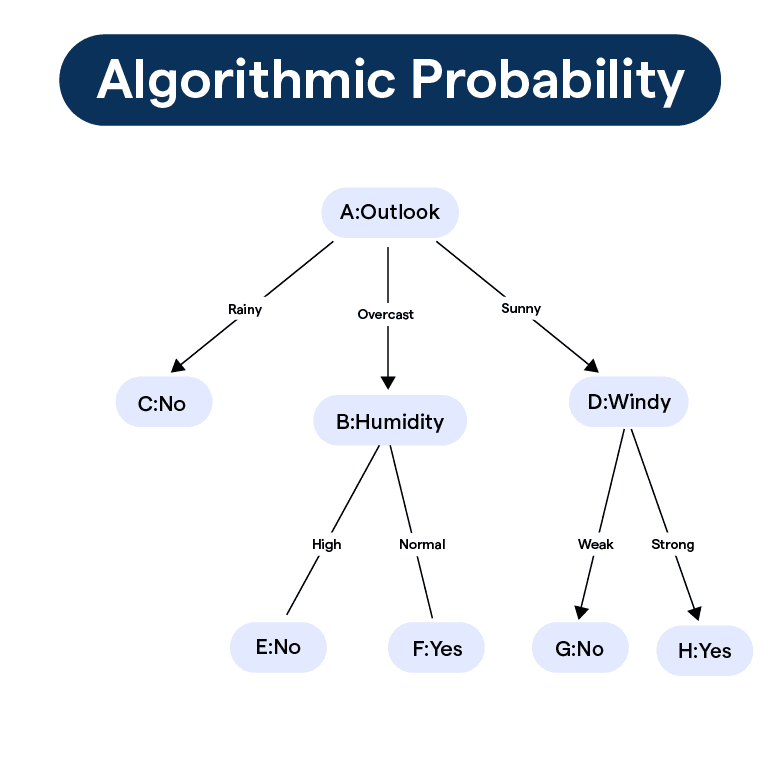
What is Algorithmic Probability?
At its core, algorithmic probability is a theory that unites computation and probability theory. It offers a method to estimate the probability of a given string of data or an event based on the length of the shortest program that can generate it on a universal Turing machine.
Infinity and Beyond
It's critical to read between the lines and recognize that algorithmic probability offers us a deep dive into infinities. Because it deals with infinite sets and possibilities, calculus and its infinite series logic play a key role in the actual calculations.
The Shortest Program Notion
A key principle underpinning algorithmic probability is that of the shortest program. The idea is that the most likely outcome corresponds to the shortest program that produces that outcome. This idea is a nod to the concept of "Occam's razor," where the simplest explanation tends to be the correct one.
Uncomputability Paradox
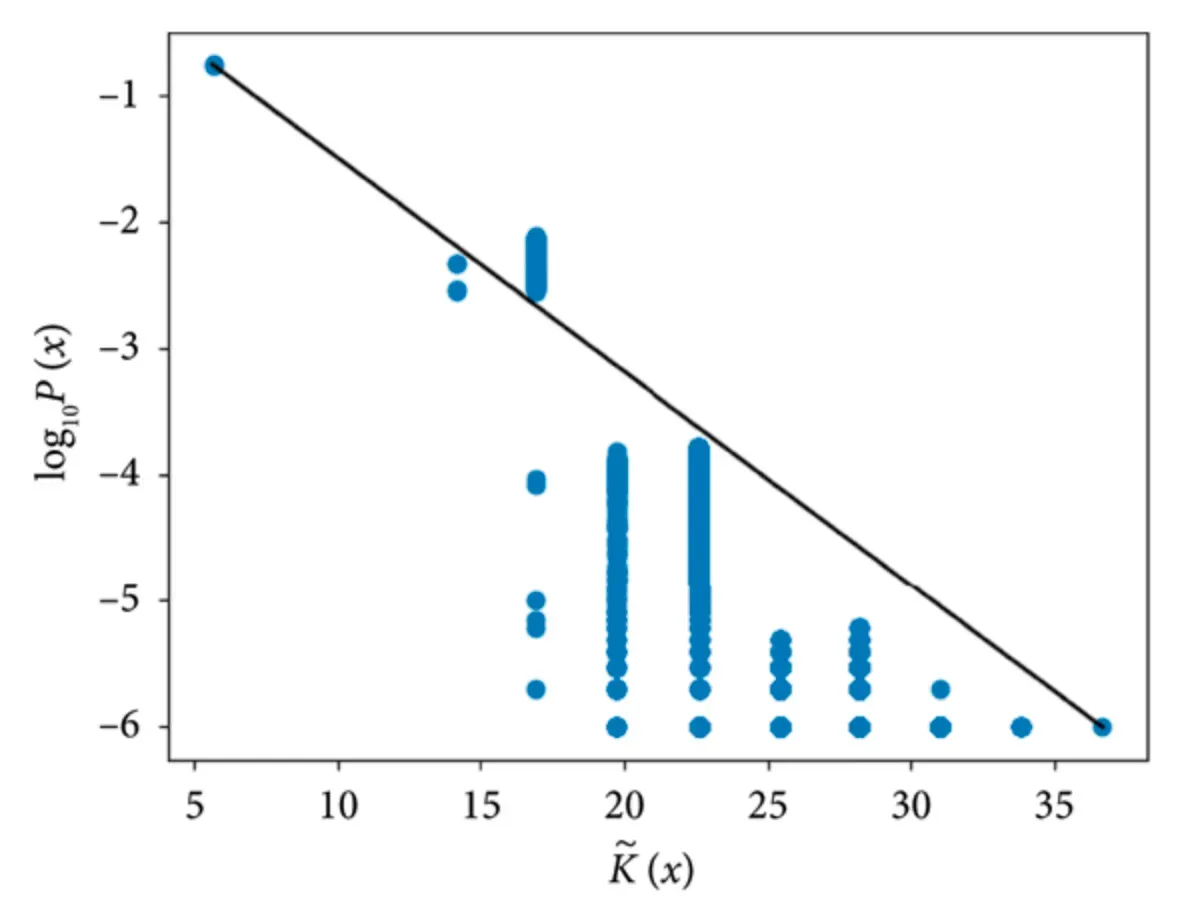
Despite its compelling mathematical elegance, algorithmic probability comes with a paradox—it's uncomputable. This means that for any given string, no algorithm can definitively compute its exact algorithmic probability.
The Turing Machine
Let's get better acquainted with a key player in algorithmic probability: the Turing machine.
Turing Machine Basics
The Turing machine, named after its creator Alan Turing, is a theoretical computing machine. It manipulates symbols according to a set of rules and serves as a model for how computations are made.
Turing Machination in Algorithmic Probability
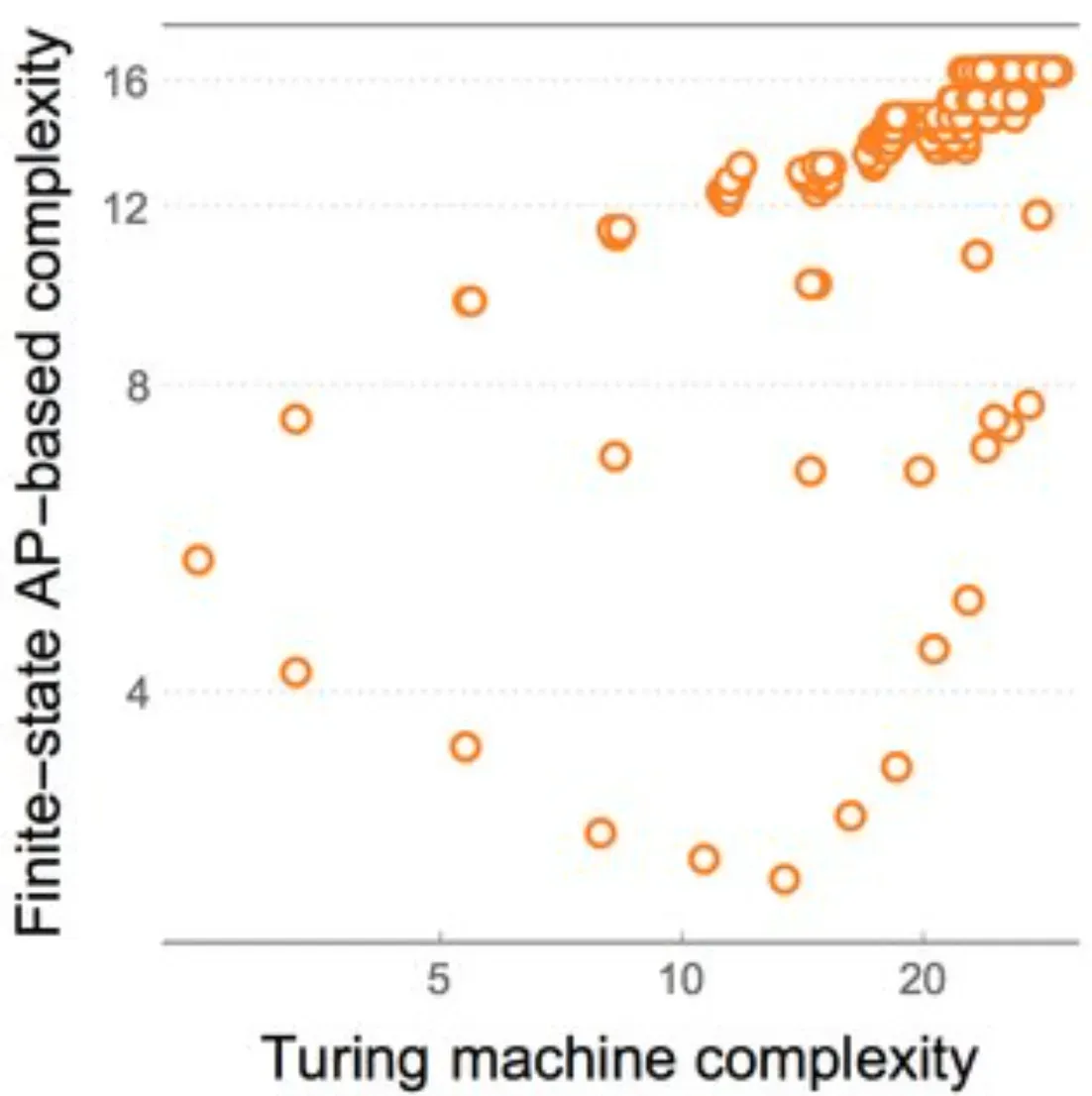
In discussions of algorithmic probability, we often talk about 'universal Turing machines.' These special Turing machines can simulate all other Turing machines, and they're the playground for programs with differing lengths and corresponding probabilities.
Universality and Invariance
One interesting property here is invariance. Despite different universal Turing machines having different sets of probabilities for the same outputs, the probability distributions tend to converge as the length of programs increases.
Turing Machines and Real-World Computing
Despite being a purely theoretical concept, Turing machines serve as a fundamental model for real-world computers. Understanding them helps computer scientists uncover the principles underlying effective algorithms.
How is Algorithmic Probability Used?
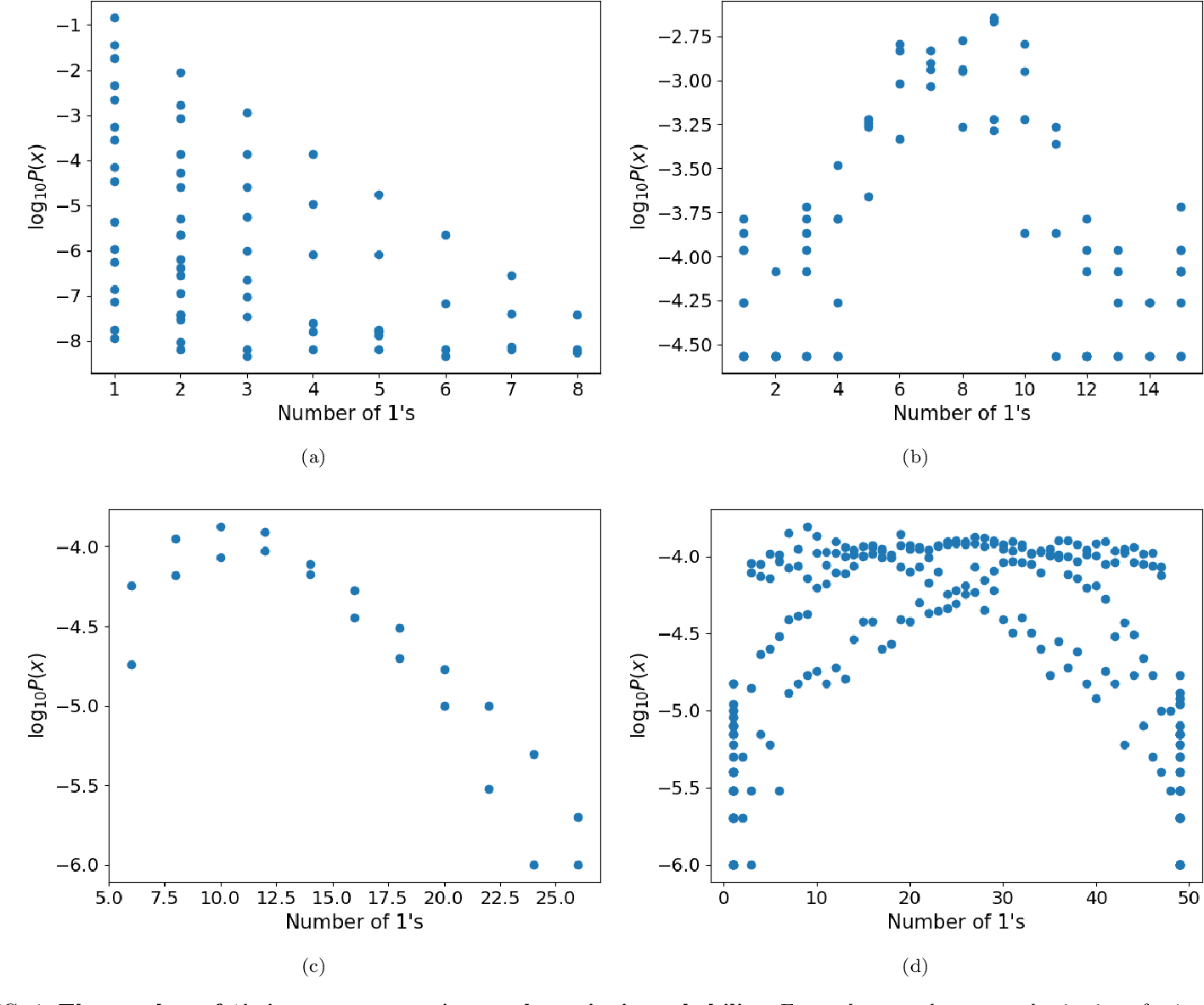
Algorithmic probability may seem abstract, but it paves the way for some fascinating applications.
Machine Learning Influence
Algorithmic probability plays a crucial role in machine learning, providing a theoretical foundation and guiding principle for developing learning algorithms.
Implications for AI
In AI, algorithmic probability helps shape intelligence systems and decision-making mechanisms. AI models, influenced by algorithmic probability, can reason inductively about the future outcomes based on past experience.
Use in Data Compression
The principle of algorithmic probability can be employed in data compression. Here, the motive is to develop the smallest program or representation possible for a given data set, following the direct parallel with the shortest program notion.
Informing Cybernetics
Algorithmic probability has also influenced the field of cybernetics, where it's used to build more robust and adaptable systems that can predict and respond effectively to changes in their environment.
Navigating Challenges: The Complexities of Algorithmic Probability
While it's a powerhouse of insight, algorithmic probability also poses complex challenges.
Dealing with Infinite Sets
As mentioned, algorithmic probability dives into the realm of infinite possibilities, and dealing with these in actual calculations can get extremely dicey.
Fruits of the Paradox
The uncomputability of algorithmic probability is a fundamental paradox that's challenging to navigate. While it sparks intriguing research questions and fuels theoretical exploration, it also limits its practical applications.
Computing Power Limitations
To put algorithmic probability to work, demanding computational power and resources are required. This restraint becomes particularly evident when dealing with large datasets.
The Complexity of Real-World Data
The challenge of dealing with real-world data, with all its noise and inconsistencies, is another hurdle in fully utilizing algorithmic probability. Finding the shortest, simplest representation of complex data is inherently a tough problem.
How Does Algorithmic Probability Relate to Other Concepts?
How does algorithmic probability integrate with—or stand apart from—other key probability or computational theories?
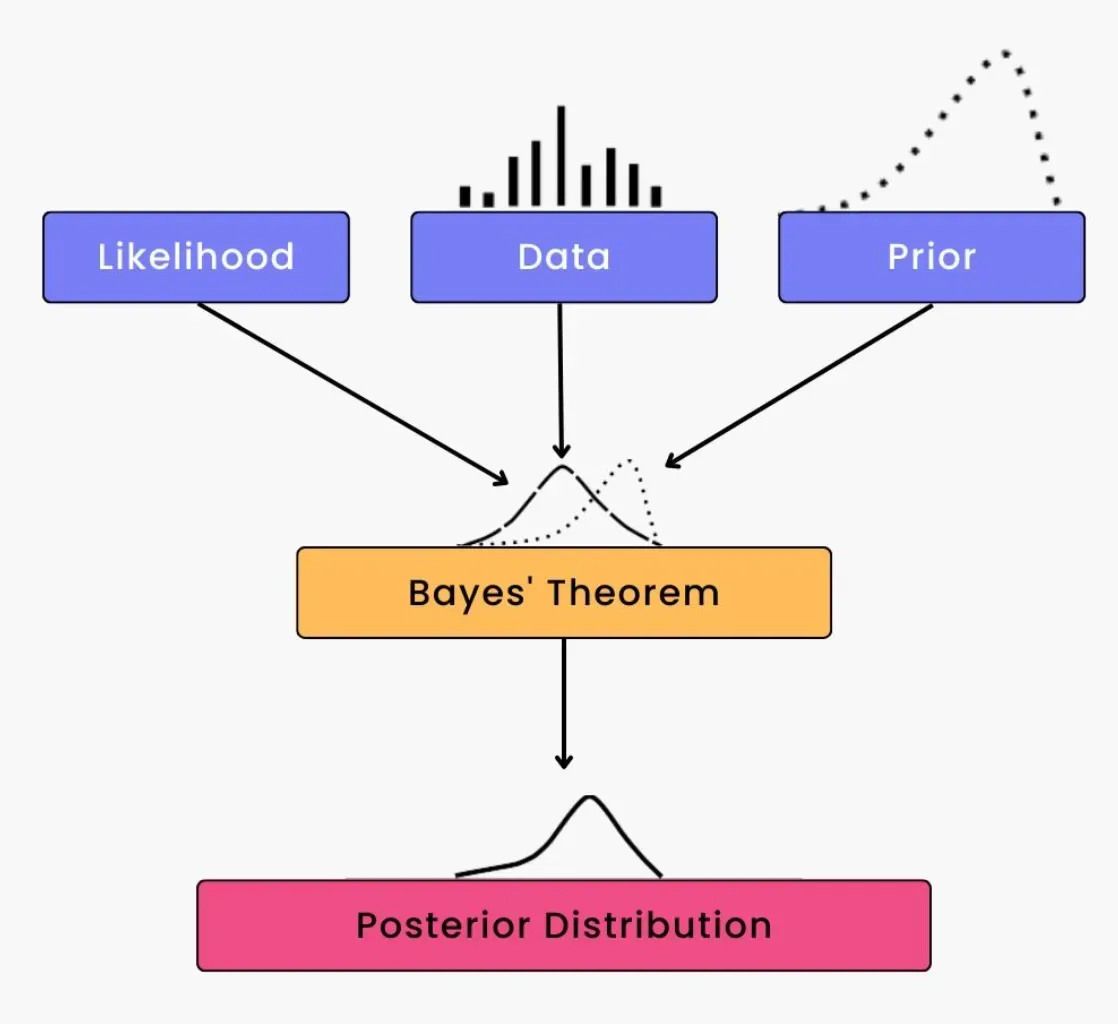
Relationship with Bayesian Probability
Algorithmic probability can be seen as a twist on Bayesian probability, merging it with the computational perspective. The shortest program principle mirrors the Bayesian likelihood, providing an algorithmic spin on predicting future events based on prior knowledge.
Different from Classical Probability
Algorithmic probability diverges from classical probability which is built around equally likely events. In algorithmic probability, events are not equally likely; instead, their likelihood is tied to the complexity of the program that generates them.
Algorithmic Information Theory
Algorithmic probability is undoubtedly linked to algorithmic information theory, as both deal with the representation and complexity of data in terms of algorithms.
Concepts of Randomness
Algorithmic probability also offers unique insights into the concept of randomness. According to this perspective, a string (or event) is deemed random if no program significantly shorter than the string itself can generate it.
Frequently Asked Questions (FAQs)
What is Algorithmic Probability?
Algorithmic Probability is a theoretical approach that combines computation and probability to predict the likelihood of a given piece of data based on the length of the shortest algorithm that could produce it on a Universal Turing Machine.
Who developed the concept of Algorithmic Probability?
The concept of Algorithmic Probability was developed by mathematician and computer scientist Ray Solomonoff in the 1960s.
How does Algorithmic Probability relate to Machine Learning and AI?
Algorithmic Probability forms a theoretical base for developing learning algorithms. In AI, it helps shape intelligence systems and decision-making mechanisms, allowing AI models to reason inductively about future outcomes based on past experiences.
What is the paradox of Algorithmic Probability?
Despite its mathematical elegance, algorithmic probability is uncomputable. This means that for any given string or data, no algorithm can definitively compute its exact algorithmic probability.
How does Algorithmic Probability connect with the Turing Machine?
Algorithmic probability is fundamentally tied to a 'universal Turing machine.' The probability of an outcome corresponds to the shortest program that can generate that outcome on such a machine. Different universal Turing machines might assign different probabilities, but these distributions tend to converge for larger-sized programs.