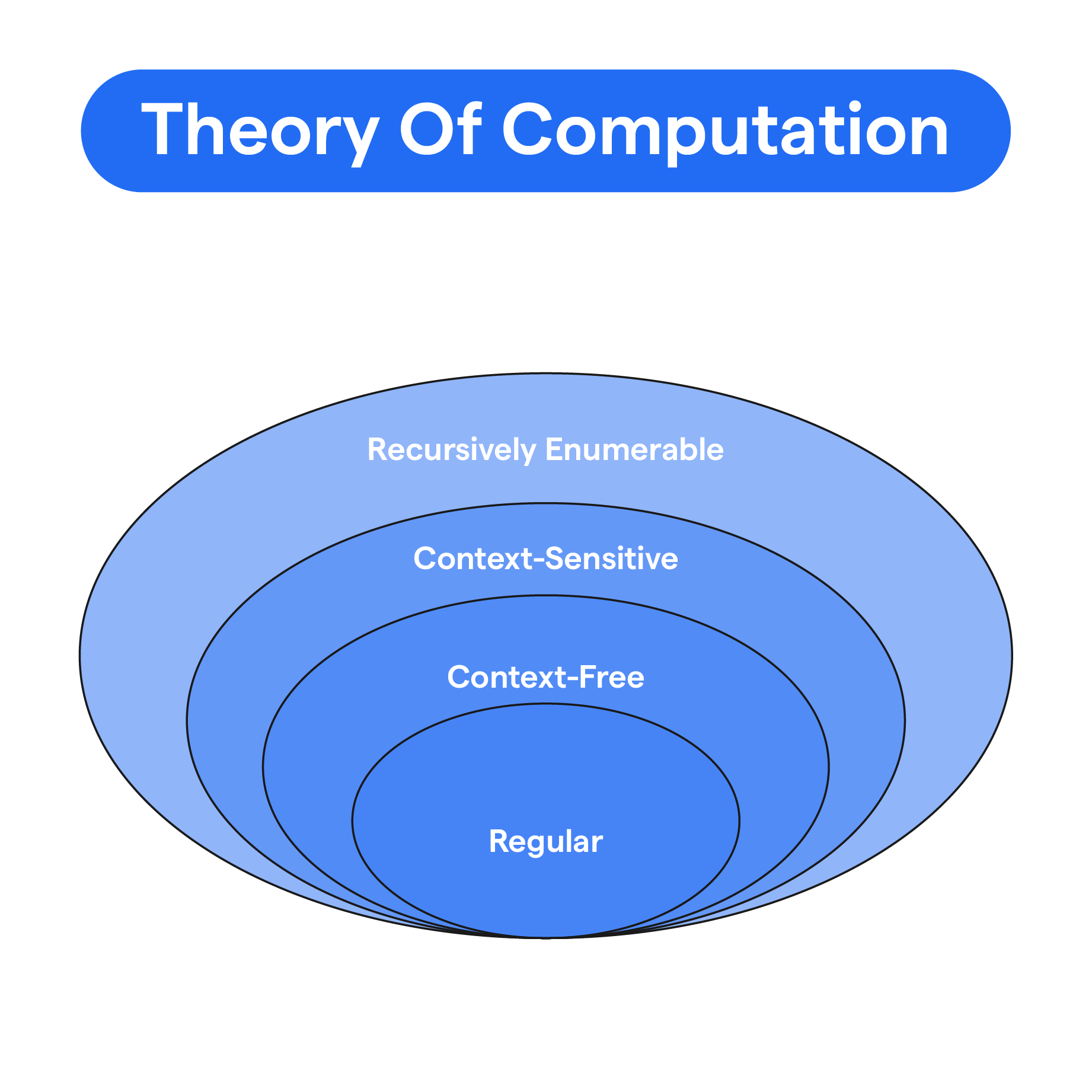
What is Theory of Computation?
The Theory of Computation is a branch of computer science that deals with how efficiently problems can be solved on a model of computation using an algorithm.
Basics in Theory of Computation
Key basics include subjects like
- Automata
- Formal languages
- Computability
- Complexity
- Algorithms
Importance of Theory of Computation
The Theory of Computation helps in providing the foundation for designing and understanding computing systems and algorithms.
Impact of Theory of Computation
It is among the foundational streams in Computer Science degrees and has wide-ranging implications from compilers to cryptography.
Who Developed the Theory of Computation and When?
The Theory of Computation was developed in the 20th century, grounded in the works of great mathematicians and logicians like Alonzo Church, Alan Turing, and John von Neumann.

Alan Turing's work on computation and his conceptual machine, now called the Turing Machine, forms one of the pillars of this theory.
Alonzo Church's Lambda Calculus was another foundational development leading to the birth of the Theory of Computation.
Today, the Theory of Computation is recognized as a distinct discipline within Computer Science, and witnessed significant developments since the 1930s and 1940s.
Why is the Theory of Computation Important?
Let's explore the importance and significance of the Theory of Computation in context.
The Theory of Computation provides a logical foundation to understand what is computable, how efficiently it can be computed, and what isn’t computable.
- Limitations and Potential of Computation: It allows us to comprehend the limitations and potential of computation, which forms the bedrock of virtually every technology today.
- Classification of Problems: The Theory of Computation plays a vital role in classifying problems based on their inherent complexity and computational resources required.
- Decision Making and Optimization: It guides us in making decisions and optimizations, shedding light on algorithmic efficiencies.
- Pioneering Advances in Computation: By understanding the basics of computation, we can pioneer advances in computation, such as quantum computing.
Where is the Theory of Computation Applied?
Now let's see how and where the Theory of Computation finds its applications.
- Computer Science and Engineering: The Theory of Computation is fundamental to Computer Science and Engineering. It provides the theoretical basis around which the entire discipline is built.
- Software Design and Development: In software design and development, it guides in understanding the inherent computational complexity and choosing the appropriate algorithmic strategies.
- Compiler Design: In compiler design, automata and formal languages, key components of the Theory of Computation, are used.
- Cryptography and Security: The Theory of Computation has significant implications in cryptography and security—in understanding what makes a cryptographic protocol secure and computationally hard to break.
- Quantum Computing: In the growing field of quantum computing, the Theory of Computation provides the groundwork for understanding the landscape of quantum computation.
How is the Theory of Computation Implemented?
Understanding how is crucial to comprehend the practicality of the Theory of Computation.
- Determining Computational Complexity: Through established theories like P vs NP, we can determine the computational complexity of problems, and know whether they are solvable in polynomial time or not.
- Designing Efficient Algorithms: The Theory of Computation helps in designing efficient algorithms by knowing the inherent complexity of problems and finding more efficient algorithms if possible.
- Using Formal Languages and Automata: Through the use of formal languages and automata, the Theory of Computation comes into play while designing and implementing compilers, interpreters, and text processing tools.
- Implementation in Security Protocols: The Theory of Computation is implemented while designing unbreakable security protocols through computational hardness.
- Challenges and Unsolved Problems: The implementation also means tackling challenges and pondering unsolved problems such as the P vs. NP question, which has significant practical implications.
Fundamental Concepts in Theory of Computation

Understanding the key elements or fundamental concepts in the Theory of Computation.
Formal Languages and Grammars
Formal languages are studied as part of the Theory of Computation, providing an accepted set of strings.
Grammars generate these strings, and the association between languages and grammars lies at the heart of understanding computation.
Computability Theory
In Computability Theory, we study what can be computed and what cannot.
Automata Theory
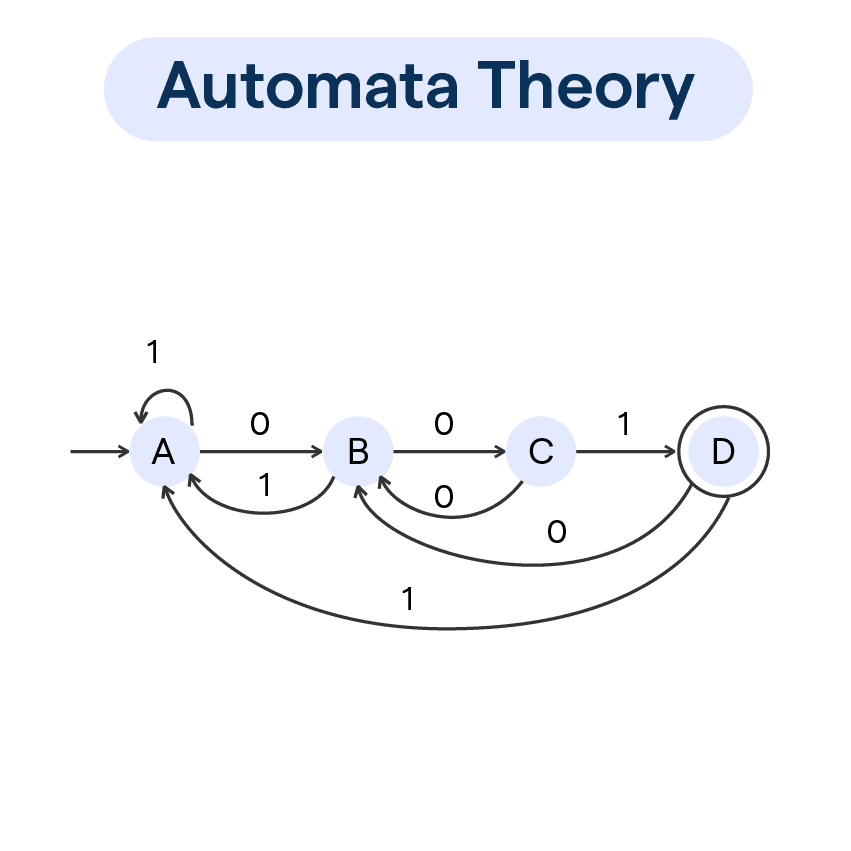
Automata theory involves the study of abstract machines and the computational problems that can be solved using these machines.
Quantum Computation
Quantum computation, while still in its infancy, attempts to understand what can be computed using a quantum model of computation.
Complexity Theory
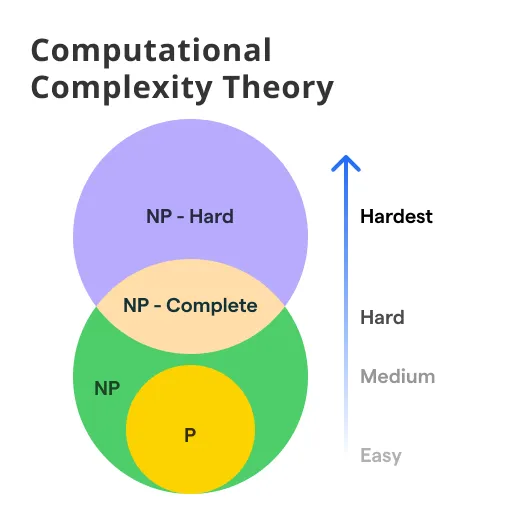
Complexity Theory involves the study of computational resources needed to solve a given problem, classifying problems into feasible and infeasible problems.
Noteworthy Theorems in Theory of Computation
Discussing some of the groundbreaking theorems in the Theory of Computation.
Church-Turing Thesis
The Church-Turing Thesis suggests that any real-world computation can be translated into an equivalent computation involving a Turing machine.
Rice's Theorem

Rice's Theorem states that properties of Turing-recognizable languages are non-trivial.
Undecidability of Halting Problem
One of Turing's key breakthroughs was proving the halting problem is undecidable.
Finite Automata and Regular Language Theorems
There are several key theorems related to finite automata and regular languages, such as the Pumping Lemma for regular languages.
P vs NP Problem
The P vs NP problem, which remains among the most significant open problems in computer science, questions whether problems whose solution can be checked quickly (NP) can also be solved quickly (P).
Major Issues and Controversies in Theory of Computation
Examining the debates within the Theory of Computation.
P vs NP Problem
The P vs NP problem remains a major unresolved issue and a subject of intense research and debate, especially its implications for cryptography.
Continued Relevance of Theory
The argument over the continued relevance of the Theory of Computation in a world dominated by machine learning and data science is a current debate.
Determinism vs Non-Determinism
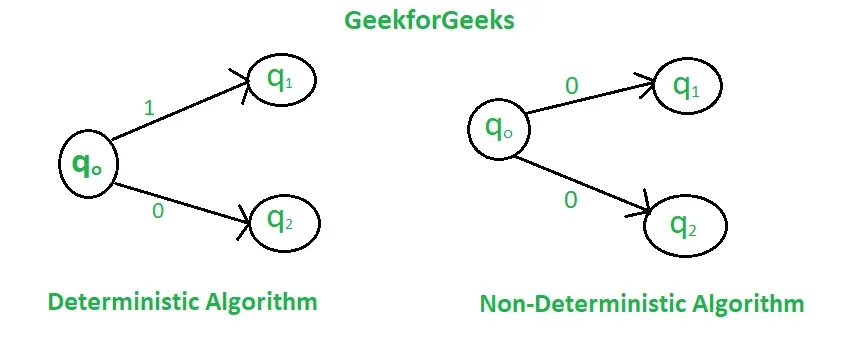
The nuanced understanding and implications of the power of determinism vs non-determinism in computational models is another area of ongoing exploration.
Quantum Computing's Promises and Challenges
The emergence of quantum computing challenges the traditional Theory of Computation and promises to redefine our understanding of computation.
Ethical Implications of Computation
As computation capability continues to grow exponentially, discussions around the ethical implications and policies surrounding computational powers become more prominent.
Challenges in the Theory of Computation
Despite its maturity, the Theory of Computation still poses several challenges.
- Unresolved Problems: The most apparent challenge is the numerous open and unresolved problems in the field, the most notable one being the P vs NP question.
- Applicability in Real-world Cases: The theoretical nature of the concepts can make it challenging to find its practical, real-world applications.
- Keeping up with Rapid Evolution: The rapid evolution of computation theories, especially with introductions like quantum computation, creates an ongoing learning curve.
- Integration with Other Areas: The integration of computation theory with other areas such as machine learning, data science, and artificial intelligence presents a complex challenge.
- Understanding Quantum Computation: Quantum computation, still in its infancy, poses challenges due to its complex mathematical structure and non-intuitive principles.
Frequently Asked Questions (FAQs)
What's the significance of Finite Automata in Theory of Computation?
Finite Automata represent simple computational models that help in understanding basic computational capabilities.
They model elementary computational tasks and serve as the foundation for more complex models like Turing machines.
How do Regular Expressions relate to Theory of Computation?
Regular expressions are a tool for describing regular languages in Theory of Computation.
They enable expressing patterns in strings effectively and are used as the basis for pattern matching algorithms in programming languages and text processing.
What contributions has the Church-Turing Thesis made?
The Church-Turing Thesis, a hypothesis, claims that any function computable through human calculation is also computable by Turing machines.
It forms the foundation for understanding computability and the limits of what computers can and cannot solve.
How does the Halting Problem influence Theory of Computation?
The Halting Problem, proved to be unsolvable by Turing, asserts that no general algorithm can determine whether another algorithm halts or runs indefinitely.
As a result, this problem highlights computability boundaries and inherent limitations in algorithm design.
Why do Complexity Classes matter in Theory of Computation?
Complexity classes, such as P and NP, categorize problems based on the time or resources required for their solutions.
Understanding these classes helps identify computationally feasible problems and design more efficient algorithms for solving practical concerns.