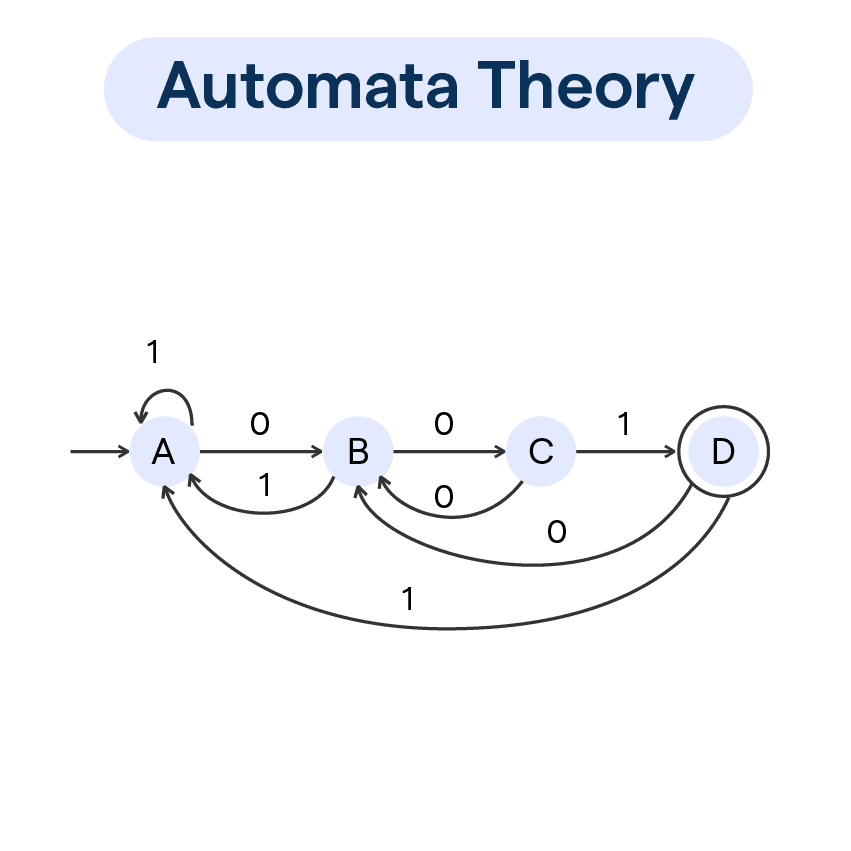
What is Automata Theory?
Automata Theory is a fascinating area of computer science that primarily deals with abstract computational devices, or "machines," and the computational problems these machines can solve. Here's a deep dive into key terms, concepts, and interesting facets of Automata Theory.
Definition of Automata
An "automaton" (plural, "automata") is essentially a self-operating machine that follows a predetermined sequence of operations. In theory, these machines can represent mathematical models of computation.
Purpose of Automata Theory
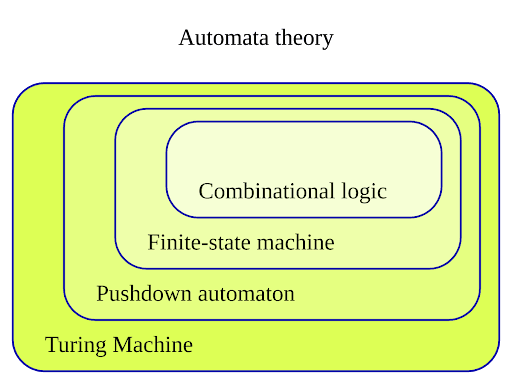
Automata Theory aims to understand and classify different computational models based on their sequential or parallel processing capabilities, symbolic density, granularity, and many other factors.
Application of Automata Theory
Automata Theory has applications across a wide range of fields, from the design of compilers and microprocessors to cryptography, natural language processing, and even biological modeling.
Key Concepts in Automata Theory
There are several fundamental concepts and types of automata that you'll encounter in Automata Theory.
Finite Automata
As one of the simplest models, finite automata are systems with a limited number of states and transitions used to model simple computational processes or devices.
Pushdown Automata
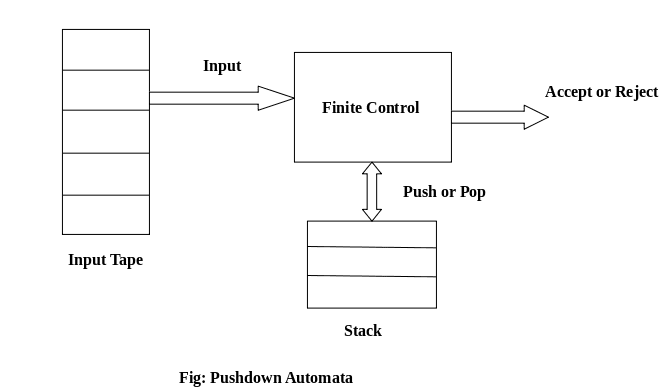
Pushdown automata incorporate an additional layer of complexity with an infinite stack in their state model, useful for processes with nested or hierarchical structures, such as syntactic analysis in compilers.
Turing Machines
These theoretical devices represent one of the most robust models of computation in Automata Theory. A Turing Machine can simulate any other automaton and forms the base of the universally accepted Church-Turing Thesis.
Formal Language Theory
Automata are often designed to work with formal languages, bringing about an intersection between Automata Theory and Formal Language Theory.
- Formal Languages: These are languages comprising sets of strings generated by specific rules or grammars. They are used in programming languages and can be processed by various forms of automata.
- Grammars: Grammars are set of production rules used to generate strings in formal languages. They're often classified according to their expressive capacity aligned with the Chomsky Hierarchy.
- Regular Expressions: Regular expressions are popular tools for describing regular languages (a subset of formal languages) and are primarily processed by finite automata.
Computation Models in Automata Theory
Automata Theory encompasses models of both sequential and parallel computation.
Sequential Computation
Sequential computation describes processes where inputs are processed one step at a time in a linear sequence. Finite Automata and Turing Machines demonstrate this type of computation.
Parallel Computation
Parallel computation integrates multiple processes at once. Models such as Cellular Automata present this concept, showing how a grid of cells changes state simultaneously according to a local interaction rule.
Non-deterministic Computation
Non-deterministic computation models allow multiple possible transitions from a given state, allowing branching paths of computation as opposed to a single, 'determined' next step.
Decidability and Complexity
Two significant areas of investigation within Automata Theory are decidability and computational complexity.
Decidability
Decidability pertains to whether a particular problem can be solved algorithmically. Some problems are undecidable, as famously demonstrated by the Halting Problem proof.
Computational Complexity
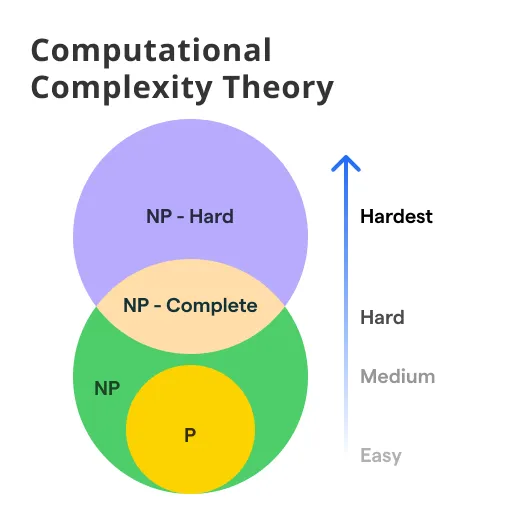
This field evaluates the resource consumption (like time or space) of an algorithm or computational process, as influenced by the input size.
Automata Theory in Practice
Automata Theory finds practical application in numerous computer science domains.
Compiler Design
Finite automata and formal grammars heavily influence compiler design, including lexical analysis and syntax parsing stages.
Pattern Matching
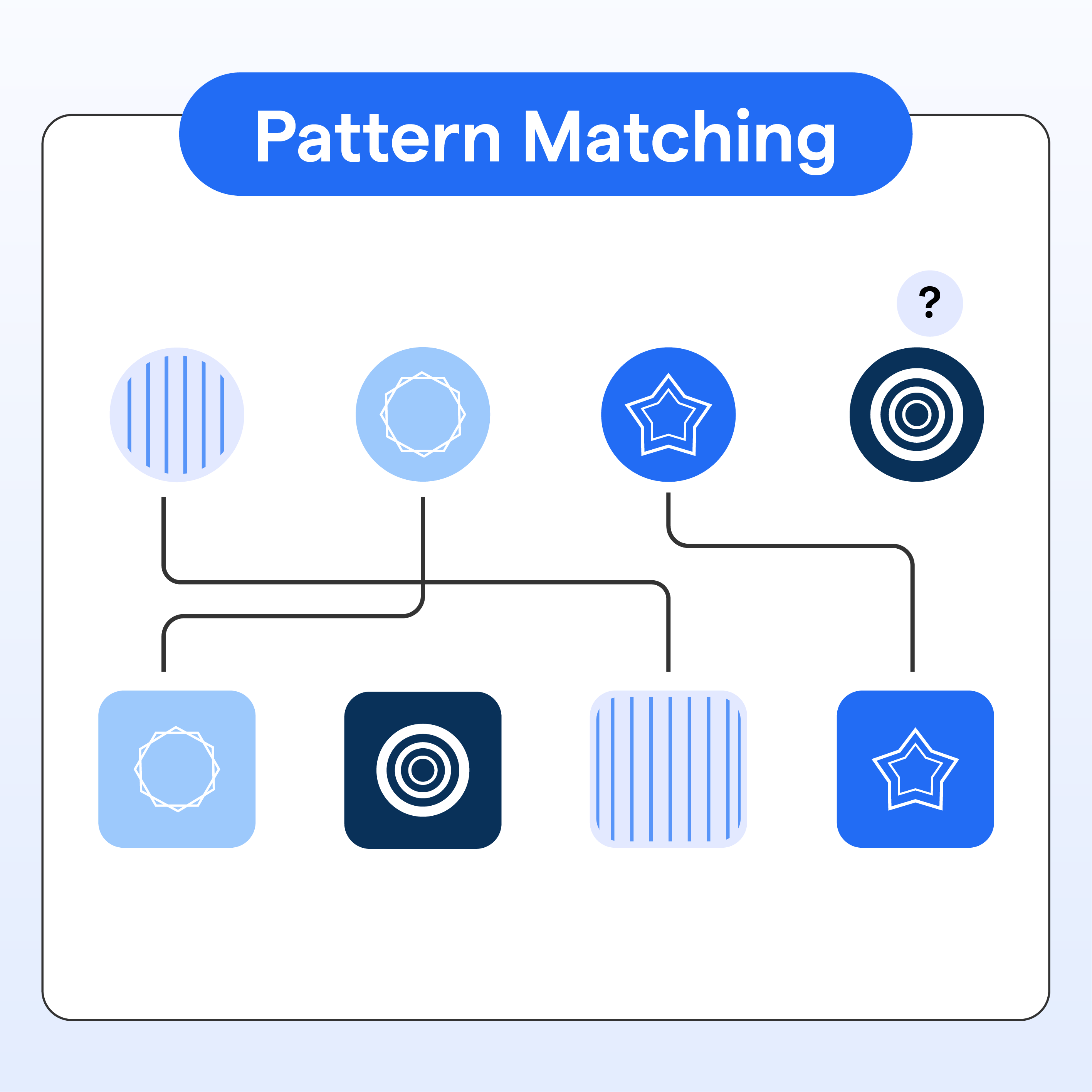
Regular expressions and automata are used in string pattern matching algorithms, a fundamental aspect of fields like bioinformatics and textual analysis.
Cyber-security
Automata Theory also influences cyber-security practices. For example, Intrusion Detection Systems use finite automata to map network behavior patterns and detect anomalies.
Frequently Asked Questions (FAQs)
What is Automata Theory?
Automata Theory is a branch of computer science that deals with the mathematical abstraction of machines, or "automata," and what computational problems they can solve.
What are some types of automata?
Key types of automata include finite automata, pushdown automata, and Turing machines. These represent different classes of computational models.
How is Automata Theory relevant to programming?
Automata Theory is fundamental to programming, especially in the design of compilers. It’s also used in pattern matching, artificial intelligence, and parsing languages.
What is the Church-Turing Thesis?
The Church-Turing Thesis proposes that any computation that can be performed by a human following a simple set of instructions, excluding resource limitations, can be executed by a Turing Machine.
How does Automata Theory affect decision problems?
Automata Theory helps classify decision problems based on their 'decidability' - whether they can be solved algorithmically. It aids in understanding the limits of algorithmic problem solving.