What is Finite Automata?
At its core, Finite Automata are simple models used to recognize patterns within input strings.
They are called "finite" because they operate with a limited, or finite, amount of memory.
These mathematical models simulate a sequence of operations, states, or conditions that are determined by a set of rules or transitions.
Concept and Definition
Finite Automata is essentially a mathematical abstraction used to design both computer algorithms and various computational processes.
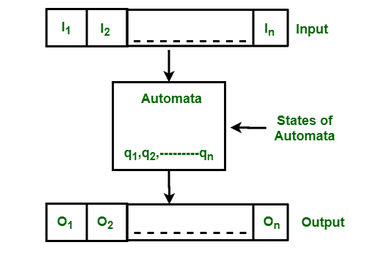
Imagine it as a blueprint that guides how a system transitions from one state to another, based on specific inputs.
Types of Finite Automata
There are primarily two types: Deterministic Finite Automata (DFA) and Nondeterministic Finite Automata (NFA).
- DFAs boast a one-to-one relationship between states and symbols, making understanding their operation straightforward.
- NFAs, on the other hand, allow for multiple transitions, adding complexity but also versatility.
Components
The primary components of FA include a set of states, a set of input symbols (also known as the alphabet), a transition function, a start state, and a set of accept states.
Operation
The operation revolves around transitioning from one state to another based on the input symbols.
The end goal is often to determine if the input string is accepted by the automata, which would mean it ends in an accepted state after processing all input symbols.
Importance
Understanding finite automata is crucial for fields like compiler design, network protocols, and even artificial intelligence, highlighting its significance beyond theoretical computer science.
Why Finite Automata?
Diving into the "why", let's explore the significance of finite automata in practical and theoretical realms.
Pattern Matching
One of the classic applications of FA is in pattern-matching algorithms. They can efficiently process text to find occurrences of a pattern, critical in fields like bioinformatics and search engines.
Language Processing
Compilers, interpreters, and other language processors widely use finite automata to parse and evaluate the syntax of programming languages, ensuring that code written by developers adheres to linguistic rules.
Network Protocol Design
FA principles are applied in designing and analyzing network protocols, ensuring data is transmitted over networks reliably and securely.
Automata Theory
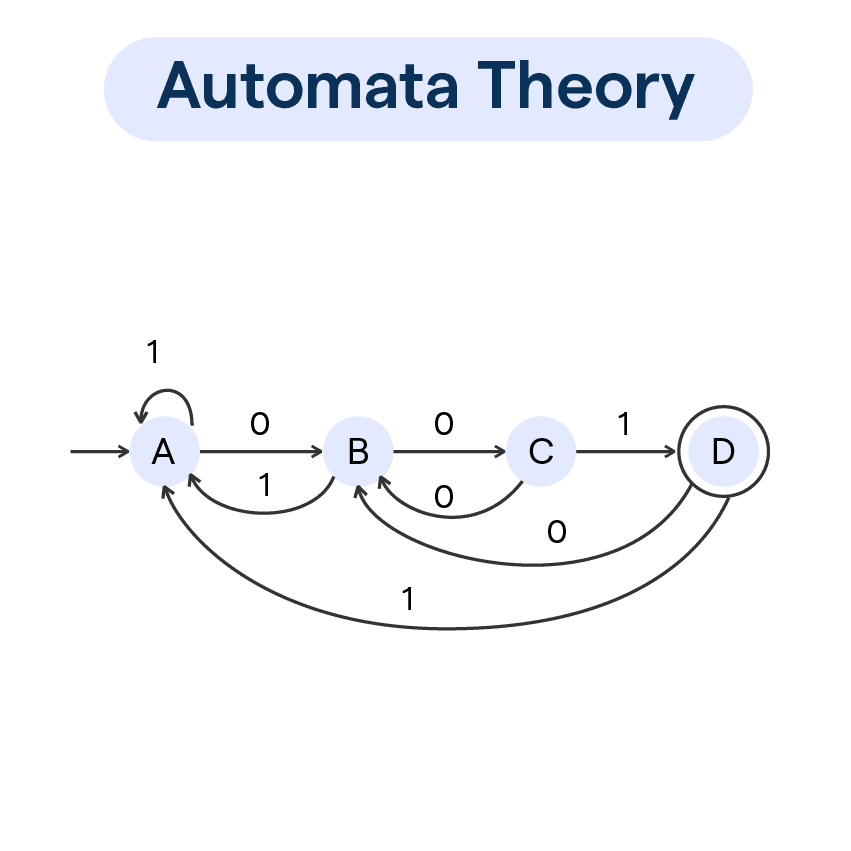
It forms the foundational stone of automata theory, a theoretical framework that explores the capabilities and limits of computing.
Educational Tool
FA serves as an excellent educational tool, helping students and newcomers understand the basic concepts of algorithm design and computational theory.
How Does Finite Automata Work?
Let's unravel the mechanism behind these mathematical models and how they translate theory into action.
Transition Function
This defines how an automaton moves from one state to another based on the input symbol it reads. It's the heart of FA, dictating the flow of operations.
Acceptance of Input
An automaton accepts input if it ends in an accept state after processing all the input symbols. This concept is crucial for validating patterns or strings in computational processes.
Deterministic vs. Nondeterministic
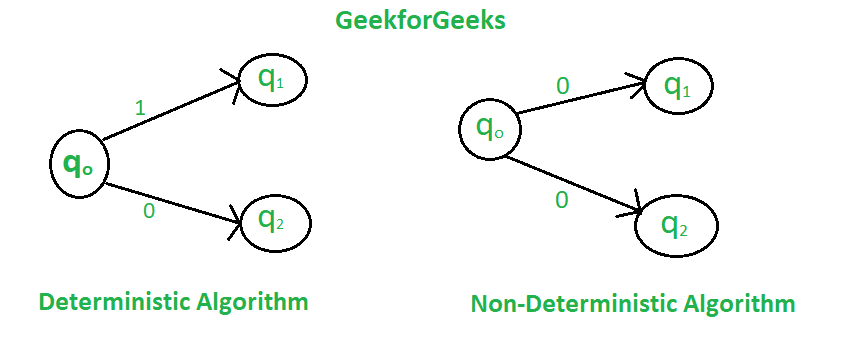
The approach to processing inputs varies significantly between DFA and NFA.
DFA's clear-cut transitions make its operation predictable, whereas NFA can explore multiple paths, making it potentially more powerful but also more complex to understand.
Closure Properties
Finite Automata exhibits closure properties under operations like union, concatenation, and Kleene star, enabling the construction of complex automata from simpler ones.
Pumping Lemma for Regular Languages
This principle offers insight into the structure of languages that can be recognized by FA, providing a means to prove whether a given language can be processed by an automaton.
When to Use Finite Automata?
Identifying the right scenarios to apply finite automata can leverage its strengths and avoid pitfalls where it might not be the best fit.
- Regular Language Identification: Whenever there's a need to process or identify regular languages, FA is your go-to model due to its inherent design for these tasks.
- Simple Parsing Tasks: For lightweight parsing needs, such as those in text processing or simple lexical analysis, finite automata can efficiently do the job.
- Protocol Design: Designing communication and network protocols often involves specifying state transitions clear-cut for FA applications.
- Educational Purposes: Teaching foundational concepts in computing, algorithm design, or even logic, finite automata provides tangible examples to learn from.
- Software Testing: Finite automata can be used to model and test software systems’ state transitions, ensuring they behave as expected under various conditions.
Who Uses Finite Automata?
While seemingly niche, the applications of FA span across various domains, illustrating its versatility and wide-ranging impact.
- Computer Scientists: At the forefront of FA applications, computer scientists employ these models for theoretical research and practical problem-solving in computer science and information technology.
- Software Developers: Developers leverage FA principles for tasks like input validation, lexical analysis in compilers, and even in designing complex game AI.
- Network Engineers: In the realm of network protocol design and analysis, engineers use finite automata to model the behavior and ensure reliability and efficiency in data transmission.
- Data Analysts: Analysts apply FA for pattern matching and data extraction tasks, especially in fields dealing with large volumes of textual data.
- Educators and Students: As an excellent educational tool, FA is widely used in academia to introduce and explore concepts in computer science and mathematics.
Trends and Innovations
Keeping an eye on the horizon, we observe evolving trends and innovations that push the boundaries of what's possible with finite automata.
Quantum Automata
Exploring the intersection of quantum computing and automata theory, quantum automata promise unprecedented computational power and efficiency.
Application in Machine Learning
Leveraging FA in machine learning, especially in natural language processing, opens up new avenues for efficient pattern recognition and linguistic structure analysis.
Enhanced Algorithm Design
Ongoing research focuses on refining and developing new algorithms to address the inherent limitations and challenges of FA, expanding its applicability.
Automata in Cryptography
The application of FA concepts in designing cryptographic protocols and analyzing security mechanisms is a growing trend, capitalizing on their mathematical rigor.
Modeling Biological Systems
Drawing parallels between biological processes and computational models, FA is increasingly used to simulate and understand complex biological systems, from genetic regulation to neural networks.
Best Practices in Finite Automata
Adhering to best practices can significantly enhance the design, understanding, and functionality of finite automata. Here are some curated tips for doing so effectively:
Start Simple
- Begin with DFA: When faced with the task of designing an automaton for a given problem, always start with a Deterministic Finite Automaton (DFA) if possible.
DFAs are easier to understand, design, and debug due to their straightforward nature—every state has exactly one transition per input symbol.
- Iterative Development: Develop your automaton iteratively, starting with recognizing the simplest forms of the desired pattern and gradually adding complexity. This approach facilitates easier error detection and correction.
Modular Design
- Leverage Closure Properties: Use the closure properties of regular languages (union, concatenation, and Kleene star) to construct complex automata from simpler ones. This modular approach enables easier maintenance and understanding.
- Component-Based Construction: Design individual components or modules for recurring patterns or functionalities. These can be reused across different automata, promoting code reuse and efficiency.
Automata Minimization
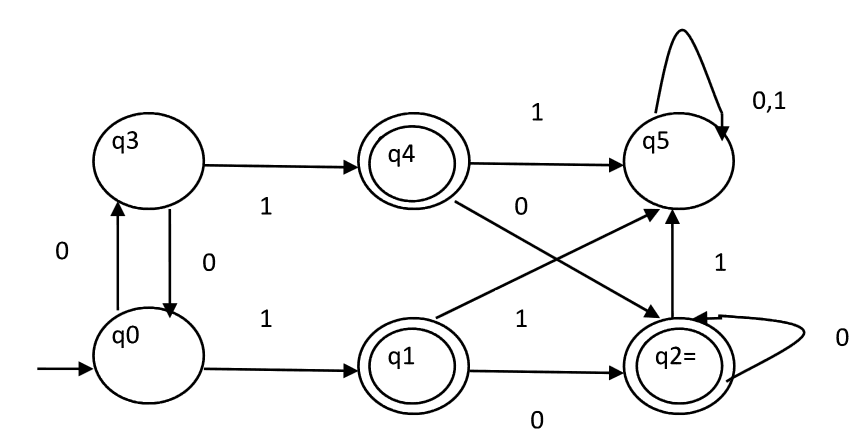
- Minimize After Design: Once you have a working DFA, apply minimization techniques to reduce the number of states and transitions. This streamlines the automaton, making it more efficient during execution.
- Leverage Minimization Algorithms: Utilize algorithms like Hopcroft's algorithm for efficient DFA minimization. This process involves identifying and merging equivalent states that lead to identical outcomes for all input sequences.
Clear Documentation
- Detailed State Descriptions: Document each state comprehensively, including its purpose and the inputs leading to and from it. This clarity aids in debugging and future modifications.
- Reasoning Behind Transitions: Document the logic or conditions behind each state transition. This is particularly helpful for non-deterministic finite automata (NFA) where multiple transitions may be possible.
Continuous Learning
- Stay Updated: The field of automata theory is ever-evolving, with new findings, optimizations, and applications being discovered. Keeping abreast of these developments can inspire innovative uses and improvements in your automata designs.
- Experimentation: Don’t hesitate to experiment with new designs or applications of finite automata. Hands-on experience is invaluable for deeply understanding the nuances and capabilities of these models.
Challenges in Finite Automata
Working with finite automata presents several challenges that can complicate their design, understanding, and implementation:
Complexity in NFA
- Managing Non-Determinism: NFAs introduce the concept of non-determinism, where multiple transitions from a state could be made based on the same input symbol.
This flexibility, while powerful, complicates the design and analysis process, making it difficult to predict and understand the automata's behavior.
Limitations in Computational Power
- Inability to Handle Context-Sensitive Languages: Finite automata are limited to recognizing regular languages. They lack the memory (or stack) necessary to process languages that require more context, such as context-free and context-sensitive languages, limiting their applicability in parsing complex syntactic structures.
State Explosion
- Designing for Complex Patterns: When an automaton is designed to recognize complex patterns, it can suffer from 'state explosion'—a rapid increase in the number of states required to accurately model the language. This escalation complicates the design and can make the automaton inefficient.
Non-determinism Ambiguity
- Ambiguous Outcomes: The ability of NFAs to pursue multiple pathways for a given input can lead to ambiguous outcomes, making it challenging to determine the exact path the automaton should follow to recognize a string.
Optimization
Finding the optimal balance between the complexity of an automaton and its performance is a perennial challenge. Designers strive to create automata that are both simple to understand and efficient in execution.
Examples of Finite Automata
To illustrate the concepts, practices, and challenges associated with finite automata, let's delve into some detailed examples:
Pattern Recognition: Email Validation

- Problem: Design a DFA to validate email addresses, ensuring they follow a basic format: local_part@domain.
- Implementation Challenges: The DFA must be comprehensive enough to handle various characters in the local part and domain, including periods, underscores, and hyphens. Avoiding state explosion while ensuring accuracy is challenging.
- Best Practices: Starting with a simple DFA that recognizes the '@' symbol and then iteratively adding complexity for period placement and character allowance can streamline the process. Minimization post-design removes redundant states, optimizing the DFA.
Network Protocol: TCP Handshake
- Problem: Model the TCP three-way handshake using an automaton to establish a connection between a client and server.
- Implementation Challenges: The automaton must accurately represent the state transitions involved in SYN, SYN-ACK, and ACK packet exchange while handling potential packet loss or duplication.
- Best Practices: A modular design approach can model individual packet exchanges as separate automata components, later combining them for the complete handshake process. Detailed documentation of each transition's meaning (e.g., "waiting for SYN-ACK after sending SYN") aids in clarity.
Educational Tool: Teaching Basic Logic Gates
- Problem: Use finite automata to teach the functioning of basic logic gates (AND, OR, NOT).
- Implementation Challenges: Converting the logic gate operations into state transitions that can be easily understood by students without a background in automata theory.
- Best Practices: Start with the simplest gate (NOT) to introduce the concept of transitions based on input bits. Use clear, concise documentation to explain how transitions represent gate operations. Iterative addition of complexity allows students to build understanding progressively.
Frequently Asked Questions (FAQs)
What is Automata Theory?
Automata theory is a branch of computer science that studies abstract machines (automata) and their capabilities.
It's the foundation for understanding how computers process information and helps design efficient algorithms
How does Finite Automata Work in Formal Language Theory?
In formal language theory, finite automata interpret symbols from an alphabet to determine if strings belong to a language, based on a set of states and transitions.
What is the Difference Between Deterministic and Non-deterministic Finite Automata?
Deterministic Finite Automata (DFA) have only one transition for each state and symbol, while Non-deterministic Finite Automata (NFA) can have multiple transitions.
Can Finite Automata Recognize Regular Languages?
Yes, finite automata are specifically designed to recognize regular languages, helping in language acceptance or rejection decision-making.
What's the Role of Transitions in Finite Automata?
Transitions guide the finite automaton from one state to another based on the input symbol, determining the path through the automaton.
What is the Final State of a Finite Automaton?
The final state also called an "accepting state," is where the automaton ends after processing the input string. If the final state is within the set of accepting states, the string is accepted.