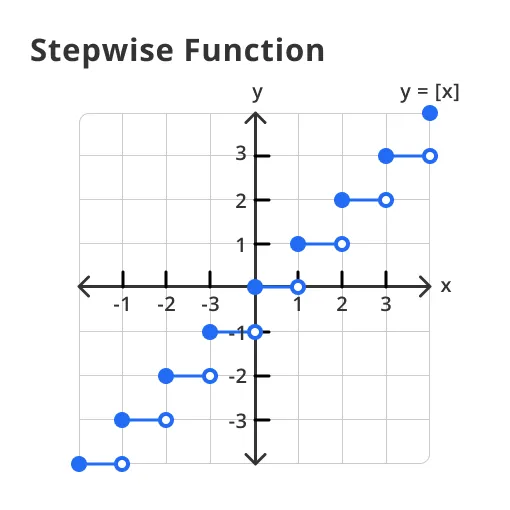
What is a Stepwise Function?
A stepwise function, also known as a step function or staircase function, is one of the most fundamental concepts in calculus and mathematical analysis.
A stepwise function is a type of function that is constant within certain intervals. It's called a "step" function because its graph looks like steps on a staircase, with each "step" corresponding to a specific interval.
Characteristics of Stepwise Functions
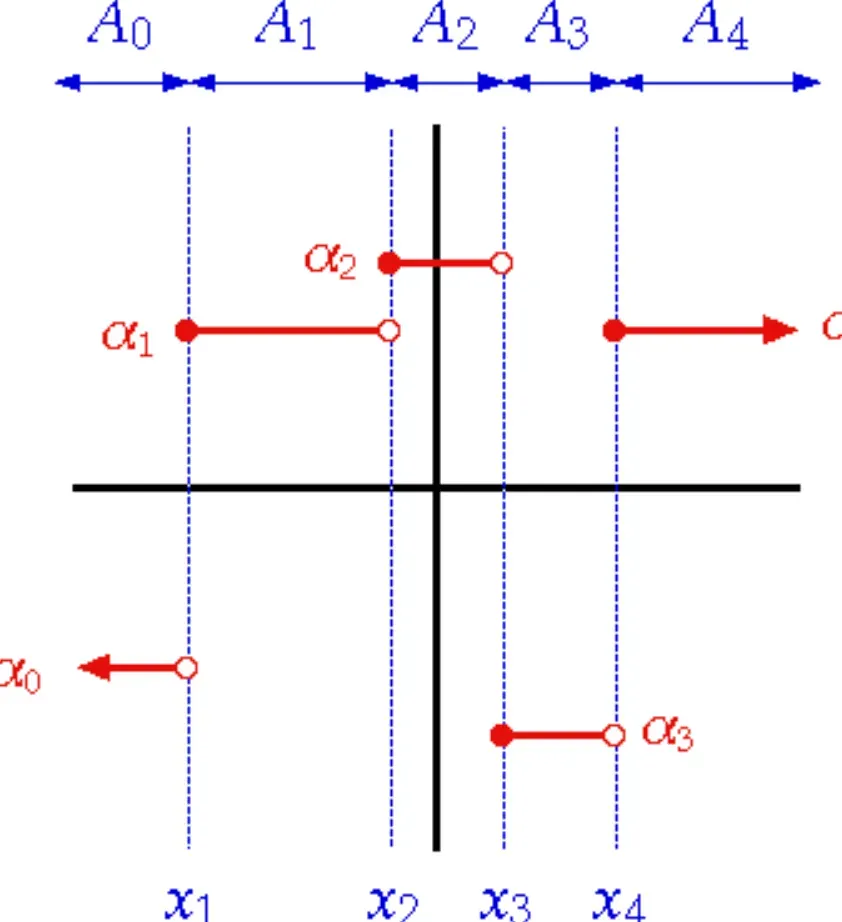
The primary characteristic of a stepwise function is the existence of constant values for different intervals of the independent variable. This means that within these intervals, the function’s value remains unchanged.
Types of Stepwise Functions
There are different types of stepwise functions, each with its distinct properties. Some commonly known types include floor function, ceiling function, and greatest integer function.
Importance in Mathematics
Stepwise functions are a core part of calculus, number theory, and other branches of mathematics. They facilitate understanding piecewise continuous functions and concepts like integrals and limits.
Real-World Applications
Stepwise functions are widely used in real-world applications, such as calculating taxes, fares, and other segmented pricing strategies.
Who uses Stepwise Functions?
Stepwise functions are extensively used in a multitude of domains and disciplines. Let's discuss the various professions and domains where step functions are of key importance.
Mathematicians
Mathematicians are the primary users of stepwise functions. These functions are employed to represent various phenomena, solve mathematical problems and understand abstract concepts.
Engineers
Engineers, particularly electrical and mechanical engineers, use step functions to represent signals and system responses.
Economists
Economists use step functions to model different economic situations where values stay constant over a range and then suddenly change.
Computer Scientists
Computer scientists use step functions, especially the floor and ceiling functions, during mathematical computations and algorithm design.
Educators
Educators use stepwise functions to teach complex mathematical concepts to students in an easily understandable form.
When to use Stepwise Functions?
Stepwise functions come into play under various scenarios, primarily when we need to represent or model certain real-world or abstract systems.
Representing Piecewise Constants
Stepwise functions are used when we need to represent piecewise constant functions, where the function's value remains constant over certain intervals.
Approximating Continuous Functions
In calculus, step functions play a pivotal role. They are used to approximate continuous functions, leading to the concept of integration.
Modeling Signal Processing
In engineering, particularly in signal processing, step functions are used to model unit step signals.
Implementing Pricing Models
Stepwise functions are used in economics and commerce to implement various pricing models and strategies.
Education and Training
In an educational context, stepwise functions are used as teaching aids for explaining complex mathematical concepts.
Where are Stepwise Functions Used?
From theoretical mathematics to practical, real-life applications, the use of stepwise functions is wide and varied. Let’s look at where stepwise functions are used in more detail.
Mathematical Theories
Stepwise functions are ubiquitous in many branches of mathematics, including calculus, number theory, and analysis.
Engineering Fields
Engineering fields, especially mechanical and electrical, use stepwise functions to model physical systems and signal responses.
Economic Modelling
Economists use stepwise functions to construct economic models where variables change at different levels of income, output, or other factors.
Commerce and Business
Businesses and commerce sectors use stepwise functions in pricing strategies where prices are constant over certain quantities and suddenly rise or drop beyond those limits.
Education and Research
Institutions dealing with mathematics education and research make extensive use of stepwise functions in teaching and academic investigation.
Suggested Reading:
Why use Stepwise Functions?
Stepwise functions are valuable mathematical tools for several reasons. They connect discrete and continuous aspects of mathematics, making them advantageous in different areas.
Simplification of Complex Concepts
Stepwise functions simplify complex mathematical phenomena, making them easier to understand and interpret.
Facilitation of Real-World Modelling
With their ability to mimic abrupt changes, step functions can be essential in representing real-world scenarios like segmented pricing models.
Basis for Important Mathematical Concepts
Stepwise functions are foundational for many mathematical concepts such as the integral, helping shape our understanding of calculus.
Widely Applicable
Given their wide range of applications across fields like engineering and economics, stepwise functions are valuable across various domains.
Conceptual Understanding
Step functions enhance conceptual understanding of mathematical and practical themes by bringing in clarity and simplicity.
How to Create a Stepwise Function?
Creation of a stepwise function involves deciding over which intervals the function will be constant, and then defining the function accordingly.
Determining Intervals
Decide over which intervals you want the step function to be constant on the x-axis (the domain).
Setting Function Values
For each of these intervals, assign a constant value that the function will take.
Using Mathematical Notation
Use proper mathematical notation to write down the step function. It is usually written in a piecewise manner.
Drawing the Graph
To visualize a stepwise function, you can draw its graph using the intervals and constant values you've defined.
Applying in Real Scenarios
Step functions can be easily built and applied in various real-life scenarios like calculating fares, data analysis, or signal processing.
Best Practices While Using Stepwise Functions
When working with stepwise functions, a few best practices can guide you to use them efficiently and correctly.
Proper Interval Selection
While defining a stepwise function, proper selection of intervals is crucial. It ensures that the function correctly represents the scenario you're modeling.
Clarity in Defining Constants
The constant value assigned to each interval should be defined clearly and unambiguously to avoid confusion.
Correct Mathematical Notation
Use correct mathematical notation while writing out stepwise functions. Misuse of notation could result in misunderstanding and incorrect solutions.
Visual Representation
Always consider drawing the graph of a stepwise function for visual understanding and verification.
Regular Practice
Like any other mathematical concept, regular practice is key to mastering stepwise functions.
Challenges in Using Stepwise Functions
Despite their usefulness, stepwise functions may present some challenges when it comes to their practical implementation.
Mathematical Complexity
While step functions are simpler than most other functions, they can still present a challenge for beginners, especially when dealing with complex interval selections.
Difficulties in Real-Life Applications
Applying step functions in real-life scenarios like economic modeling can be tricky as it often requires careful consideration of the intervals and constant values.
Understanding Mathematical Notations
The mathematical notation used to represent step functions could be confusing initially, particularly for those new to such concepts.
Graphical Interpretation
Interpreting the graph of a step function might be challenging, especially when dealing with complex step functions that involve overlapping intervals.
Knowledge of Foundations
Lack of foundation knowledge in calculus and mathematical analysis could be a hurdle towards understanding stepwise functions, as the concept is heavily based on these principles.
Trends in Stepwise Functions
Although stepwise functions are a fundamental mathematical concept, trends in their application and use still exist and evolve with development in related fields.
Innovation in Teaching Methods
In education, new innovative methods for teaching stepwise functions are being designed to simplify complex mathematical concepts and make learning more engaging.
Application in Modern Engineering
Emerging fields like data science and machine learning are also finding unique uses of stepwise functions, displaying their enduring relevance.
Advanced Financial Modeling
In the field of finance, sophisticated models using stepwise functions are being developed to accommodate complex financial scenarios and strategies.
Use in Artificial Intelligence
In recent years, stepwise functions are finding application in the emerging field of artificial intelligence, particularly in the design and training of neural networks.
Interdisciplinary Studies
Interdisciplinary research, where fields like mathematics, physics, and computer science converge, is witnessing innovative uses and applications of stepwise functions.
Stepwise functions are an invaluable tool in mathematics, engineering, and many other fields. They reflect the beauty of mathematics, where simple structures can represent complex scenarios and ideas.
By learning about and mastering stepwise functions, we gain an appreciation of their simplicity, versatility, and the profound concepts they embody.
Frequently Asked Questions (FAQs)
What is a Stepwise Function in Mathematics?
A stepwise function is a type of function that remains constant within certain intervals of the independent variable, creating a staircase-like graph.
Are Stepwise Functions Different from Constant Functions?
Yes, while a constant function has a constant output, a stepwise function has different outputs depending on the intervals of the input.
Can a Stepwise Function be Differentiated?
Typically, stepwise functions are non-differentiable at the points of 'jump', though they are differentiable between these points.
Why are Stepwise Functions important in Real-World Applications?
Stepwise functions represent real-world situations where values change abruptly at certain intervals, like tax brackets or shipping charges.
How is Integration Applied to Stepwise Functions?
Although stepwise functions have discontinuities, they can still be integrated. The integral is usually split into integrals over each constant interval.