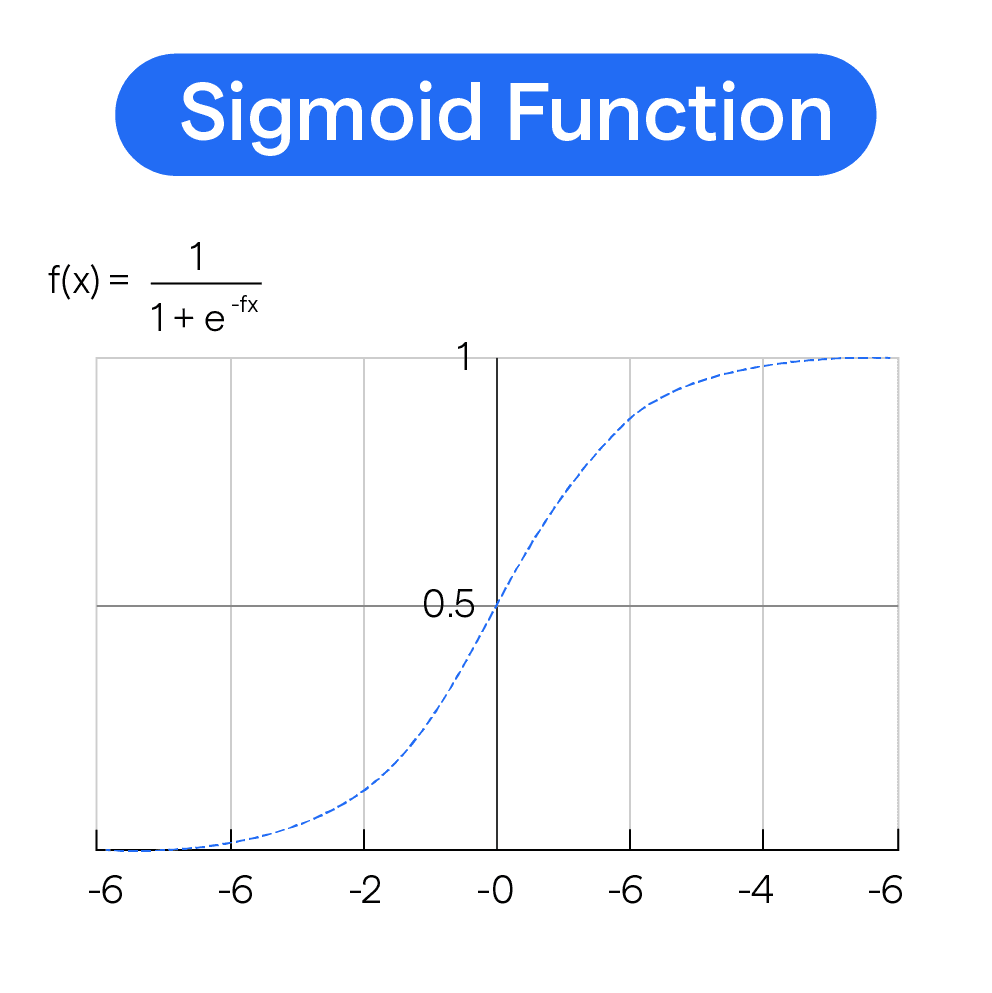
What is a Sigmoid Function?
A sigmoid function, to put it simply, takes any real value and squeezes it into a range between 0 and 1. It's like taking a zebra and turning it into a unicorn, but without the glitter and sparkles.
The most common sigmoid function is called the logistic function, which has a nice S-shaped curve.
Using some mathematical prowess, we can express it as Y = 1 / (1 + e^(-z)), where Y is the output, e is Euler's number (2.71828), and z is the input. So essentially, the sigmoid function turns your input value into a probability!
History of the Sigmoid Function
The sigmoid function has been studied for over 200 years. It was first introduced in the early 1800s by mathematician Daniel Bernoulli. Bernoulli used an early form of the sigmoid to model population growth.
In the 1870s, statistician Francis Galton built on Bernoulli's work. Galton explored sigmoid curves to represent growth and decay processes. He studied how the sigmoid could model natural phenomena.
In the early 1900s, mathematicians Pierre Verhulst and Pearl Reed further developed sigmoid models, known as the logistic function. Their work deepened understanding of the S-shaped curve and applications in statistics.
In the 1950s, statistician George Box propagated the logistic function across various fields. The sigmoid gained widespread use in econometrics and psychometrics during this time.
In the 1980s, the sigmoid saw major use in artificial neural networks. It became the standard activation function for backpropagation algorithms in deep learning. This cemented its significance in machine learning.
Today, the sigmoid remains an indispensable tool across statistics, econometrics, epidemiology, and machine learning. It continues to find novel applications in modeling natural processes and probabilities.
Types of Sigmoid Functions
In this section, we'll explore various types of sigmoid functions and their associated formulas to get a better understanding.
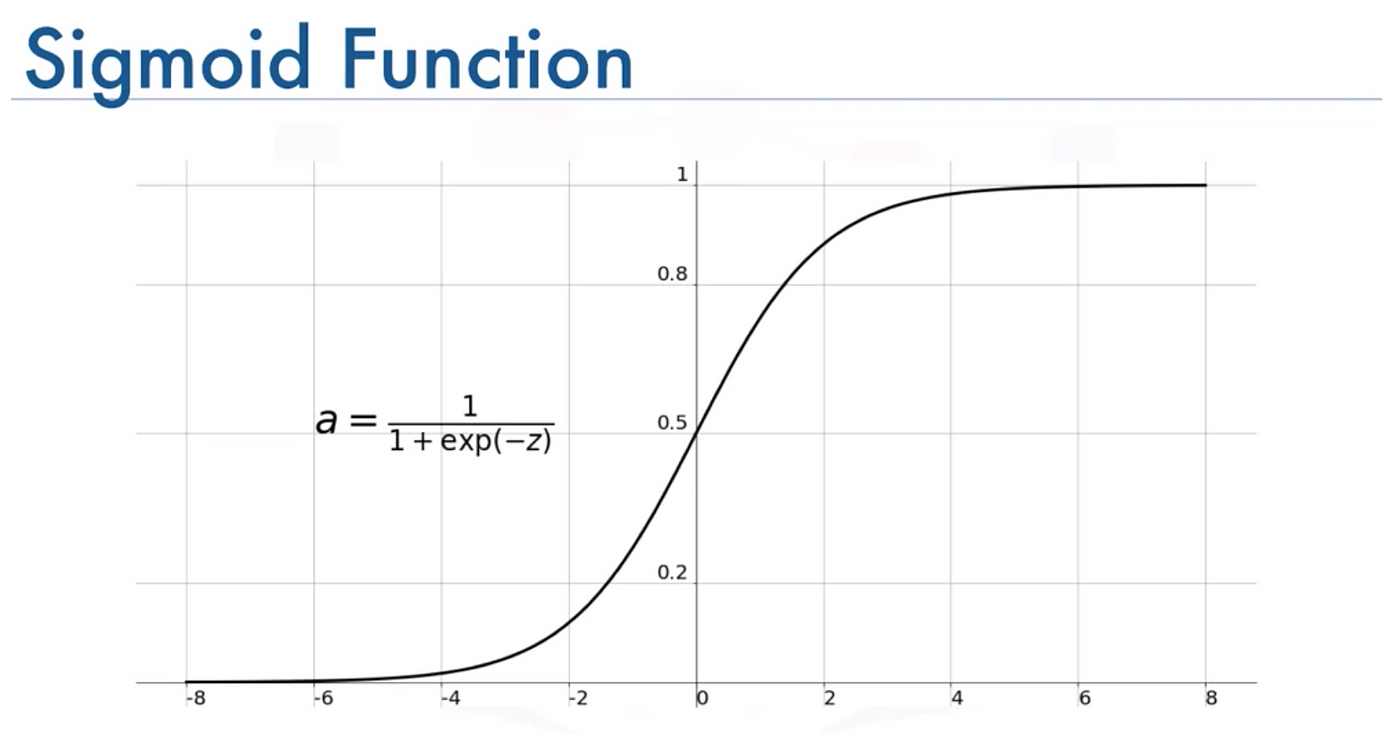
Logistic Sigmoid Function
The logistic sigmoid function is probably the most common type of sigmoid function used in machine learning, especially in binary classification problems.
Its output is limited to a range of 0 and 1, ideal for models where we need to calculate probabilities.
Formula: f(x) = 1 / (1 + exp(-x))
Hyperbolic Tangent Function (tanh)

The hyperbolic tangent function, or tanh for short, is another sigmoid function that instead maps the input values to a range between -1 and 1.
This is especially useful when the model needs to accommodate negative outputs.
Formula: f(x) = tanh(x) = (exp(x) - exp(-x)) / (exp(x) + exp(-x))
Arctangent Function (arctan)
The arctangent function, another sigmoidal function, returns values from -π/2 to π/2, and it is generally used for inverse tangent operations.
Formula: f(x) = arctan(x)
Rectified Linear Unit (ReLU)
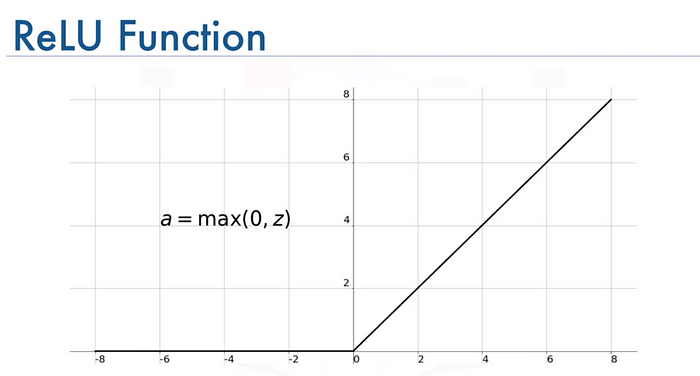
Although not technically a sigmoid function, the Rectified Linear Unit (ReLU) is an important activation function in neural networks.
It provides simplicity and improved training performance as it discards negative inputs, which can help mitigate the problem of gradient vanishing.
Formula: f(x) = max(0, x)
Leaky ReLU
Leaky ReLU is an improved version of the ReLU function that allows small, non-zero outputs for negative inputs.
This helps to address the "dying ReLU" problem, where some ReLU neurons essentially become inactive and only output 0.
Formula: f(x) = max(0.01x, x), where 0.01 is a typical value for the slope when x < 0.
Exponential Linear Unit (ELU)

The exponential linear unit (ELU) is another variant of ReLU that minimizes the vanishing gradient problem and increases the learning speed of neural networks.
Unlike the ReLU, ELU outputs negative values when input is less than zero, which allows the mean activations to be closer to zero and thus helps to push the derivatives closer to natural gradient.
Formula: f(x) = x for x > 0 and α(exp(x) - 1) for x <= 0 where α > 0.
Softplus Function
The Softplus function is another variation of the ReLU function.
It's smooth across all real-valued inputs, making it differentiable everywhere, which can be an advantage when training models that require differentiation of the activation function.
Formula: f(x) = log(1 + exp(x))
These various types of sigmoid and related functions largely determine the behavior of the artificial neurons, and in turn, play a distinct role in shaping the performance of machine learning and deep learning models.
Applications of Sigmoid Function
In this section, we'll understand the varied applications of the sigmoid function across multiple domains.
Logistic Regression

In statistics, the sigmoid function plays a crucial role in logistic regression, a technique for analyzing and modeling the relationship between multiple inputs and a binary outcome.
It aids in predicting probabilities and classifying data points.
Image Processing
In the realm of image processing, the sigmoid function is applied to transform pixel values.
This manipulation can enhance image attributes such as contrast and brightness, leading to better image quality and clarity.
Signal Processing
Utilization of the sigmoid function in signal processing helps to model how neurons transmit signals across vast biological networks.
This characteristic makes it invaluable in designing systems that mimic neural behavior, such as artificial neural networks.
Activation in Neural Networks

The sigmoid function serves as a popular activation function within neural networks in machine learning.
It transforms input values into a probability range between 0 and 1, allowing for further processing and learning from data patterns.
Economics Modeling
The sigmoid function finds its place in economics as well, where it can represent the response of economic agents to stimuli.
For example, it might be employed to model the transition of consumers between different market alternatives for a product or service.
Sigmoid Function in Deep Learning
Deep learning is the current buzzword in the world of AI, and sigmoid functions play a crucial role in this exciting field.
Let’s take an in-depth look at the sigmoid function and it’s significance in Deep learning.
Sigmoid for Binary Classification

Binary classification is the task of classifying items into one of two groups. Sigmoid function's output range of 0 to 1 is perfect for this.
It can be seen as providing a probability that an input belongs to one of the classes.
The Role of Sigmoid as an Activation Function
In the context of a neural network, the sigmoid function is popularly used as an activation function, defining the output of a node given an input or a set of inputs.
It helps to introduce non-linearity into the output of a neuron.
Benefits of Sigmoid in Deep Learning
The sigmoid function stands out for its simplicity and its differentiable nature. It's easy to compute and its output can be used to create a probability distribution for decision-making tasks.
Drawbacks and Alternatives to Sigmoid
Despite its benefits, the sigmoid function presents certain limitations such as the problem of vanishing gradients for very large positive and negative inputs.
This has led to the search for other alternatives like ReLU (Rectified Linear Unit) that don't suffer from this issue.
Frequently Asked Questions (FAQs)
What is the purpose of a sigmoid function?
Well, a sigmoid function has a rather cool role! It's mainly used to squash any real value into a range between 0 and 1. Thanks to this characteristic, it's great for estimating probabilities.
You'll often hear about its application in machine learning, especially for binary classification tasks.
How does a sigmoid function help with classification?
Ah, great question! Imagine we have the output from our sigmoid function, cruising somewhere in the range from 0 to 1. Now, we can use this output to split things into two groups.
If the output swings above 0.5, it belongs to one group; if it falls below, it's classified into the other. Neat, isn't it?
What are some common types of sigmoid functions?
Oh, there are quite a few! To name a handful, we've got the logistic sigmoid function, the hyperbolic tangent function, the arctangent function, the Guddermannian function, the error function, the smoothstep function, and the generalized logistic function.
What are the applications of sigmoid functions?
It's amazing where you might stumble across sigmoid functions. They pop up as activation functions in artificial neural networks, play an integral part in binary classification tasks, assist in image processing, and even sneak into modeling population growth.
You'll find them in economics, biology, and a whole lot more!
How does the sigmoid function fit into deep learning?
Deep within neural networks, sigmoid functions serve as the heartbeat for individual neurons, enabling them to process information and make predictions.
Their knack for delivering outputs between 0 and 1 makes them a common choice for binary classification tasks in the world of deep.