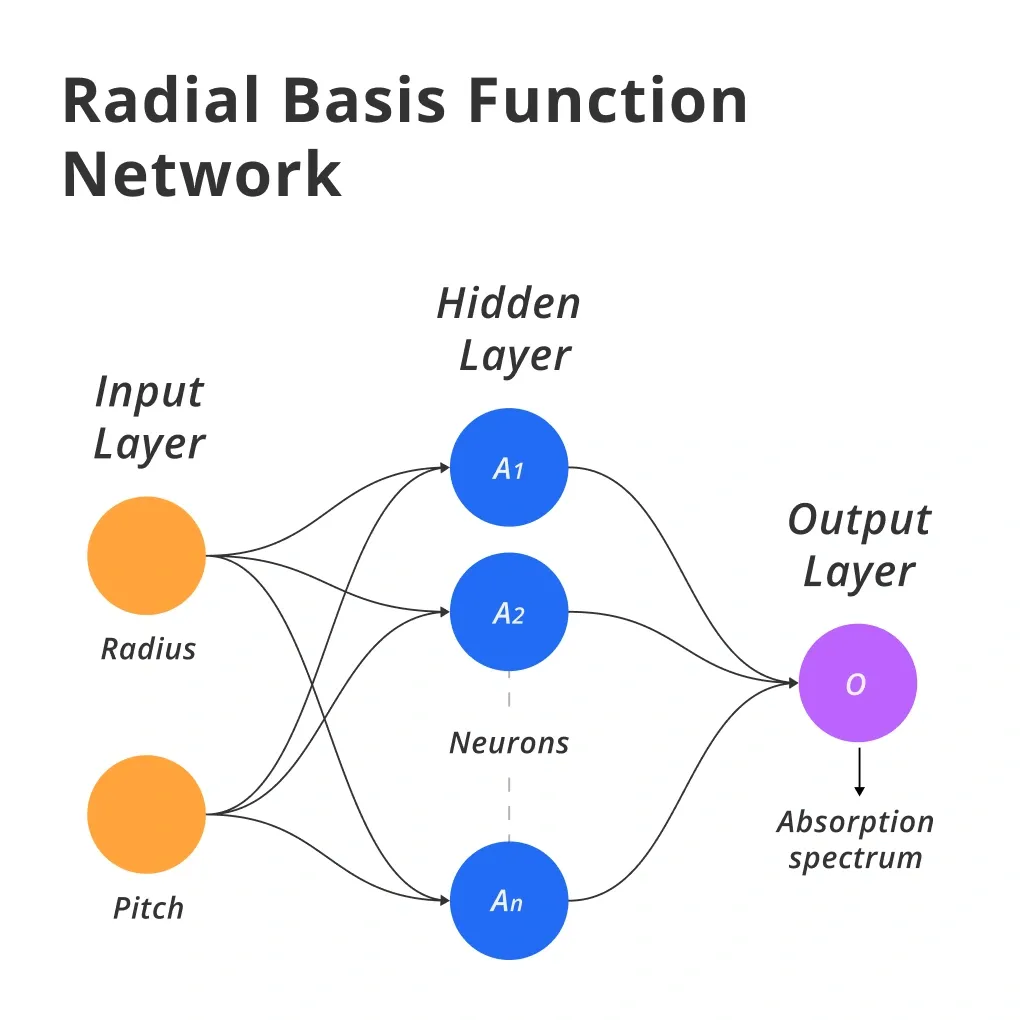
What is Radial Basis Function Network?
At its core, the Radial Basis Function Network is a type of artificial neural network that utilizes radial basis functions as its activation function.
It’s primarily used for various applications such as function approximation, time series prediction, classification, and system control.
Definition
RBFN is a network that provides a way to approximate any function that generally has real-valued vectors as inputs, using a combination of radial basis functions.
Structure
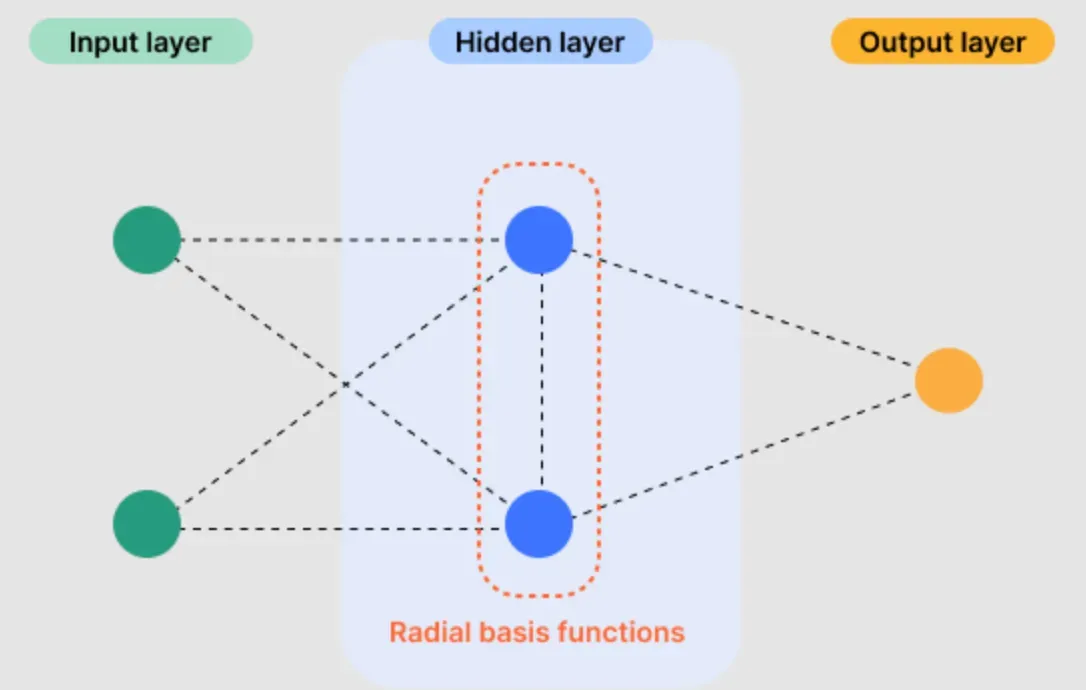
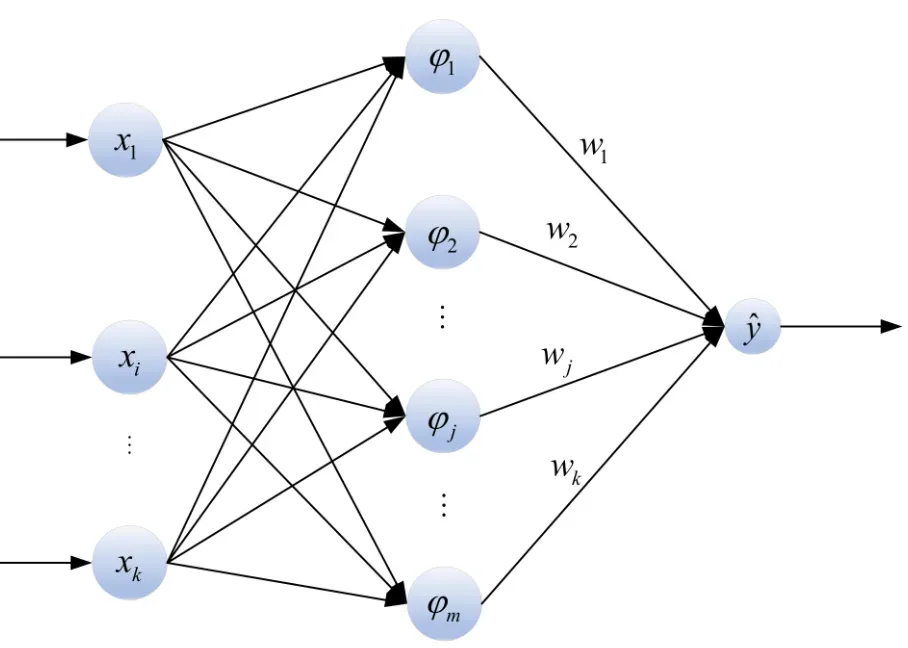
The typical structure of an RBFN consists of three layers: an input layer, a hidden layer (where the radial basis functions reside), and an output layer.
Activation Function
In RBFNs, the activation function is the radial basis function itself, which reacts to the distance of the input from a central point in a specific way.
Applications
RBFNs are widely used in pattern recognition, regression analysis, and cluster analysis, amongst other areas.
Advantages
RBFNs offer several advantages, including simplicity of design, universal approximation capabilities, and relatively fast training times compared to other types of neural networks.
Who Uses Radial Basis Function Networks?
RBFNs find their applications in a wide range of domains, from finance to robotics. Let’s look at who typically benefits from this technology.
- Data Scientists: Data scientists employ RBFNs for predictive modeling and data mining tasks, exploiting its excellent approximation capabilities.
- Financial Analysts: In the finance sector, financial analysts use RBFNs for forecasting market trends and analyzing risk.
- Research Academics: Academics and researchers in machine learning and artificial intelligence use RBFNs to explore new methodologies or enhance existing ones.
- Engineers: Engineers, especially in automation and control systems, apply RBFNs in designing and implementing intelligent control mechanisms.
- Healthcare Professionals: In healthcare, professionals use RBFNs for medical diagnosis, analysis of genetic data, and even in creating models that simulate biological processes.
Where is Radial Basis Function Network Used?
RBFNs are versatile and find usage across a plethora of fields. Here are some common applications.
Pattern Recognition
RBFNs excel in recognizing patterns and anomalies in large data sets, making them ideal for facial recognition, handwriting recognition, and more.
Forecasting
Whether it’s predicting the stock market or weather forecasting, RBFNs provide a powerful tool for analyzing historical data to predict future events.
Control Systems
In robotics and automated systems, RBFNs contribute to developing adaptive control systems that can learn and adjust to new conditions over time.
Bioinformatics
In bioinformatics, RBFNs help in understanding biological data, including DNA sequencing and protein structure prediction.
Signal Processing
RBFNs are applied in signal processing for filtering noise from signals or for compressing data without significant loss of information.
When is Radial Basis Function Network Used?
Choosing the right moment and conditions to utilize RBFNs is crucial for their effectiveness.
- Dealing With Nonlinear Data: RBFNs are particularly suitable for nonlinear data modeling, where the relationship between variables isn’t straightforward.
- High-dimensional Data: In situations where the data features are high-dimensional, RBFNs can handle the complexity efficiently.
- Real-time Prediction Needs: For systems requiring real-time predictions or classifications, the fast response of RBFNs is invaluable.
- Function Approximation: When the goal is to approximate a function closely, RBFNs are often the go-to solution due to their flexibility and accuracy.
- Sparse Data: RBFNs have a knack for working well with sparse data sets, where traditional linear methods might struggle.
How Does Radial Basis Function Network Work?
Understanding the workings of an RBFN can demystify how it manages to perform its tasks so effectively.
- Input Layer: This layer accepts the raw input data and passes it on to the next layer without any modification.
- Hidden Layer: The hidden layer transforms the input data using radial basis functions, each reacting to how 'close' the input data is to its center.
- Radial Basis Functions: These functions, typically Gaussian, compute the similarity between the input and their center points, fundamentally determining the network's output.
- Output Layer: The output layer aggregates the activations from the hidden layer and translates them into a format suitable for understanding the network's response to the input.
- Training the Network: Training an RBFN involves adjusting the center points of the radial basis functions in the hidden layer and the weights leading into the output layer to minimize the difference between the actual and predicted outputs.
Radial Basis Function Network: Best Practices
Leveraging RBFN to its fullest potential requires adherence to a set of best practices.
Choosing the Right Function
The choice of radial basis function (Gaussian, multiquadric, etc.) can significantly impact performance. Selection should be based on the specific requirements of the application.
Determining Centers and Widths
Strategically positioning the centers of the radial basis functions and adjusting their widths is crucial for capturing the nuances of the input data.
Regularization
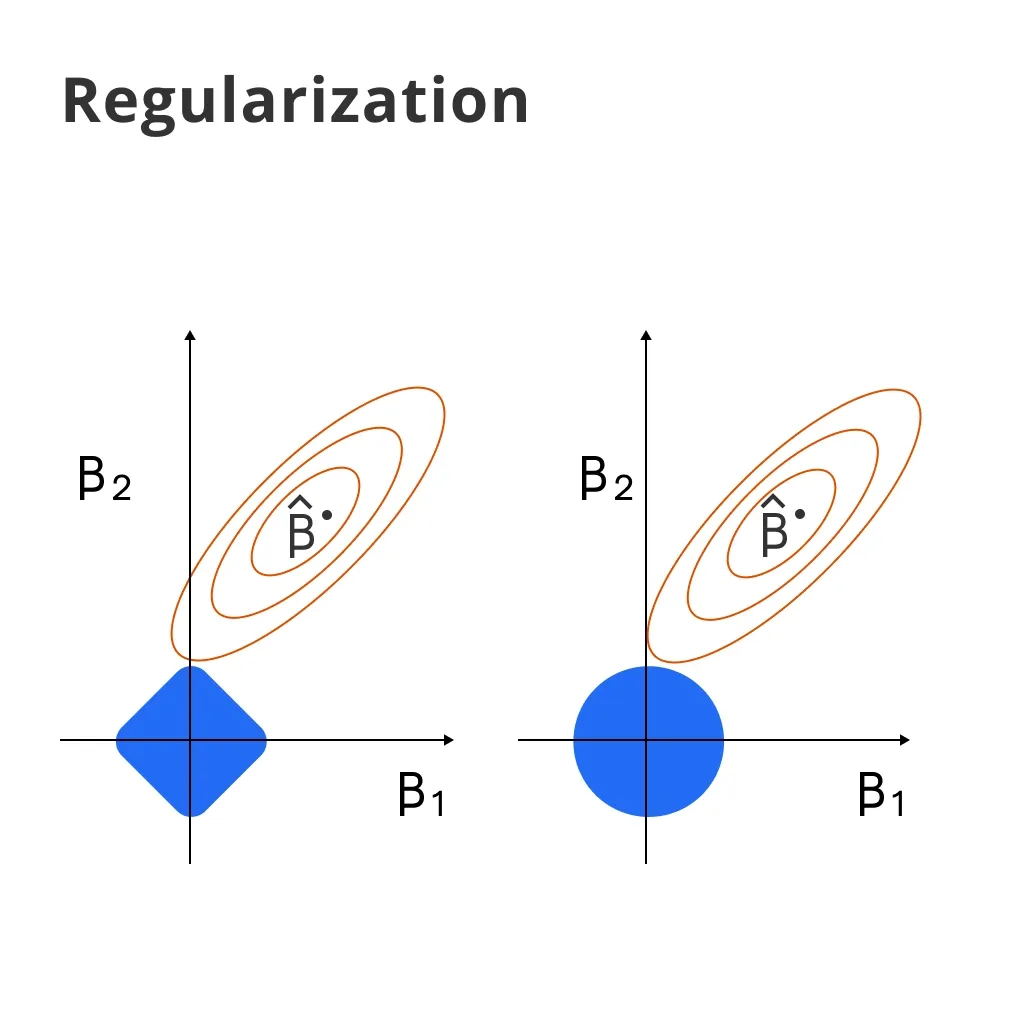
Implementing regularization techniques can help prevent overfitting, especially in cases where the data is prone to noise.
Data Preprocessing
Normalizing or standardizing input data can enhance the network’s efficiency by ensuring that variations in scale don’t skew the results.
Incremental Learning
For dynamic environments, adopting an incremental learning strategy can allow the network to adapt to new data without retraining from scratch.
Challenges with Radial Basis Function Network
Despite its strengths, RBFN comes with its own set of challenges that one needs to navigate.
- Selecting Optimal Parameters: Finding the optimal number of radial basis functions and their parameters can be a time-consuming and computationally expensive process.
- Risk of Overfitting: Given its capacity for high-dimensional function approximation, there’s a tangible risk of overfitting the model to the training data, reducing its generalization capability.
- Computational Demands: As the size of the data grows, RBFNs can become computationally intensive, requiring significant resources for both training and inference.
- Limited Interpretability: The transformations within the hidden layer can be difficult to interpret, making it challenging to diagnose why an RBFN might be making certain predictions.
- Scalability Issues: Scaling RBFNs to very large datasets requires careful management of computational and memory resources to maintain performance efficiency.
Trends Around Radial Basis Function Network
Advancements in technology and shifts in application requirements continuously shape the way RBFNs are used and developed.
Integration with Deep Learning
There’s growing interest in integrating RBFNs with deep learning architectures to leverage their respective strengths in handling complex, nonlinear problems.
Cloud Computing
The rise of cloud computing offers solutions to the computational and scalability challenges that come with RBFNs, making it more accessible to a wider audience.
IoT Applications
In the Internet of Things (IoT), RBFNs are finding applications in edge computing, where lightweight, efficient models are needed for real-time data processing.
Enhanced Algorithms
Ongoing research is aimed at developing more effective algorithms for parameter selection, training, and optimization of RBFNs, pushing the boundaries of what they can achieve.
Cross-disciplinary Applications
RBFNs are seeing increased application across various fields, from environmental science predicting climate change impacts to finance for algorithmic trading strategies, showcasing their versatility and adaptability.
Frequently Asked Questions (FAQs)
What sets radial basis function network apart from other neural networks?
Radial Basis Function Networks utilize radial basis functions as activation functions, which respond to the distance of an input from a central point, unlike other neural networks that typically use sigmoidal or ReLU activation functions.
In what kind of problems is a radial basis function network typically used?
Radial Basis Function Networks excel in interpolation problems, like function approximation, due to their ability to approximate any function closely.
How does the radial basis function network perform classification?
It classifies data by computing the similarity between an input vector and each neuron's center, making it adept at classifying patterns that are spatially clustered.
Why are radial basis function networks considered to have faster convergence?
The localized response of radial basis functions often leads to faster training and convergence compared to global functions used by other types of neural networks.
Can radial basis function networks handle high-dimensional data?
They can handle high-dimensional data, but the number of neurons — and consequently the computational complexity — may increase significantly, posing challenges.