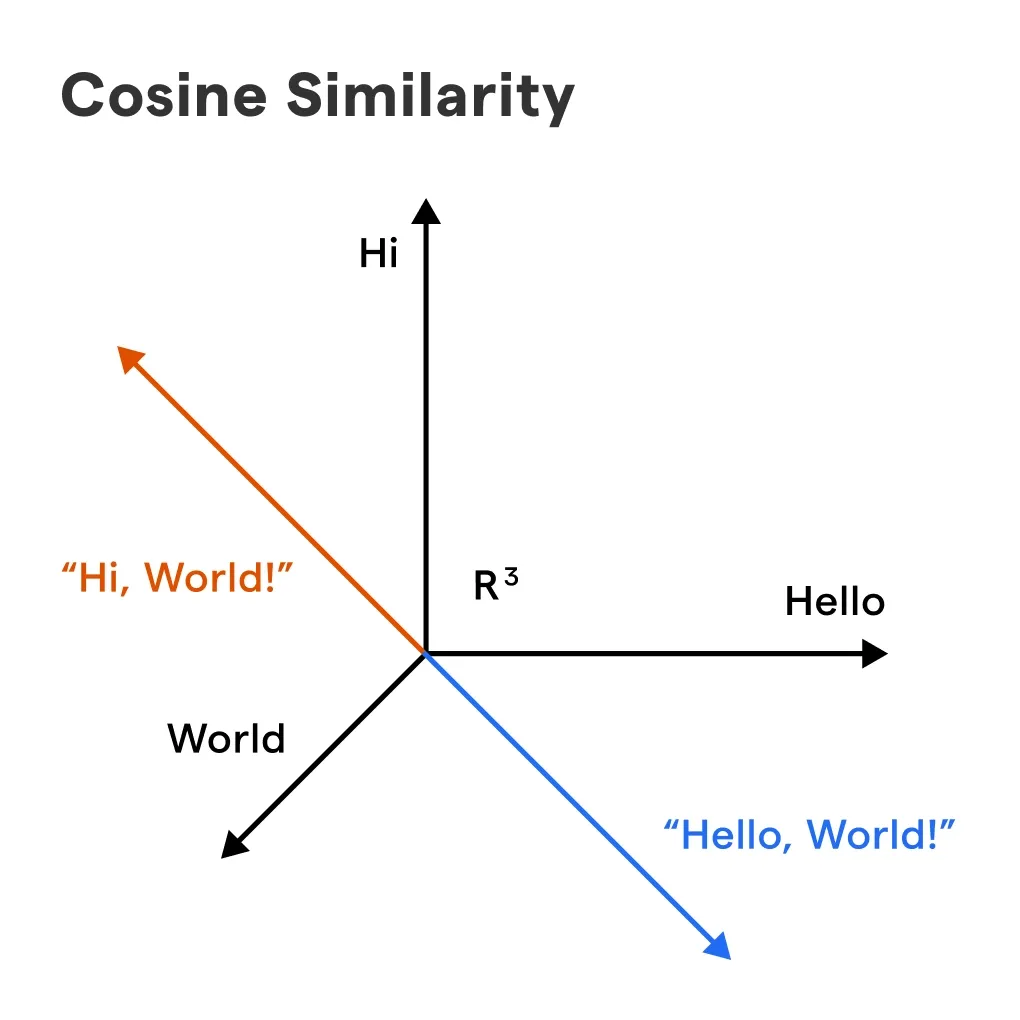
What is Cosine Similarity?
Cosine Similarity is a metric used to measure how similar two entities are. It's like a friendship test for data, but with math.
The Math Behind It
It might seem a bit terrifying, but it's just basic trigonometry. It calculates the cosine of the angle between two vectors, hence the name.
It's Core Idea
At its heart, Cosine Similarity is all about understanding the orientation rather than the magnitude. It's more interested in the direction rather than the distance.
Relation to Vector Space
Vectors aren't just for physicists. In data science, we often represent items like text or user profiles as vectors. Cosine Similarity tells us how aligned these vectors are.
Other Similarity Measures
While Cosine Similarity is great, there are others in the game too, like Euclidean distance and Jaccard similarity. Each has its niche, depending on the problem at hand.
Why Use Cosine Similarity?
Curious why Cosine Similarity is a big deal? Let's dive into what makes it such a hot favourite.
High Dimensionality Handling
Dealing with many dimensions is like juggling balls. The more there are, the tougher it gets. But Cosine Similarity handles it like a pro.
Robustness to Magnitude
Cosine Similarity cares about angles, not magnitudes. This makes it a reliable measure even when data scales vary.
Efficiency with Sparse Data
Cosine similarity tends to excel with sparse data. All those zeros? Not a problem. Like a focus lens, it zeroes in only on non-zero dimensions.
Suitable for Text Comparisons
Comparing text documents? Cosine Similarity is your partner in crime. It's often used in Natural Language Processing (NLP) to gauge document similarity.
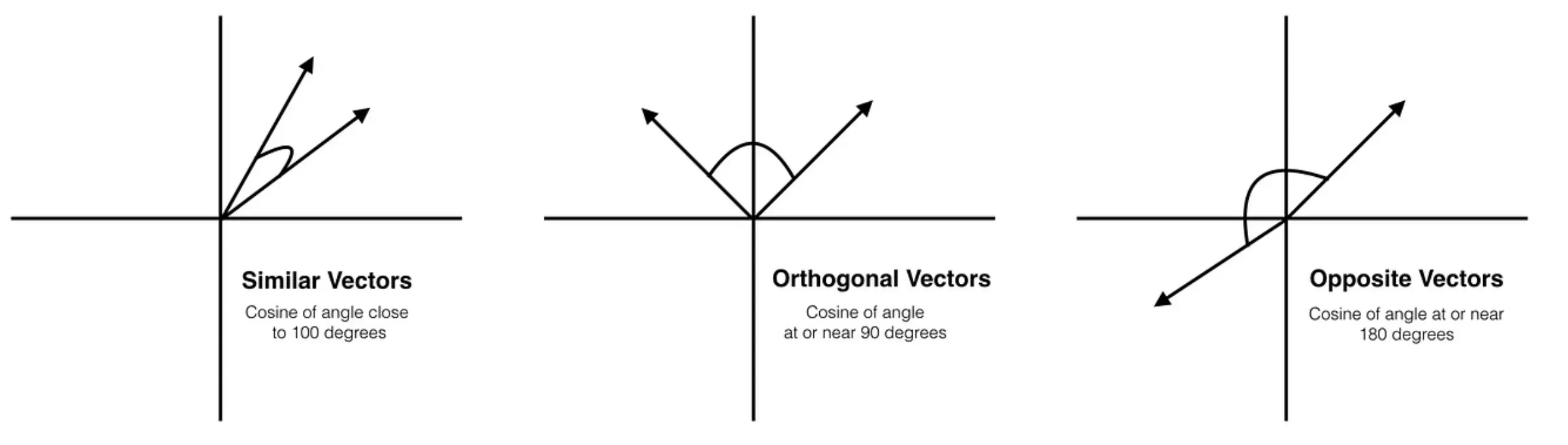
Resilience to Orthogonality
With Cosine Similarity, orthogonal vectors (those at 90 degrees) are maximally dissimilar. Makes sense, right? Different directions imply different stories.
When to Use Cosine Similarity?
Knowing when to use Cosine Similarity is as important as knowing what it is. Let's look at some scenarios.
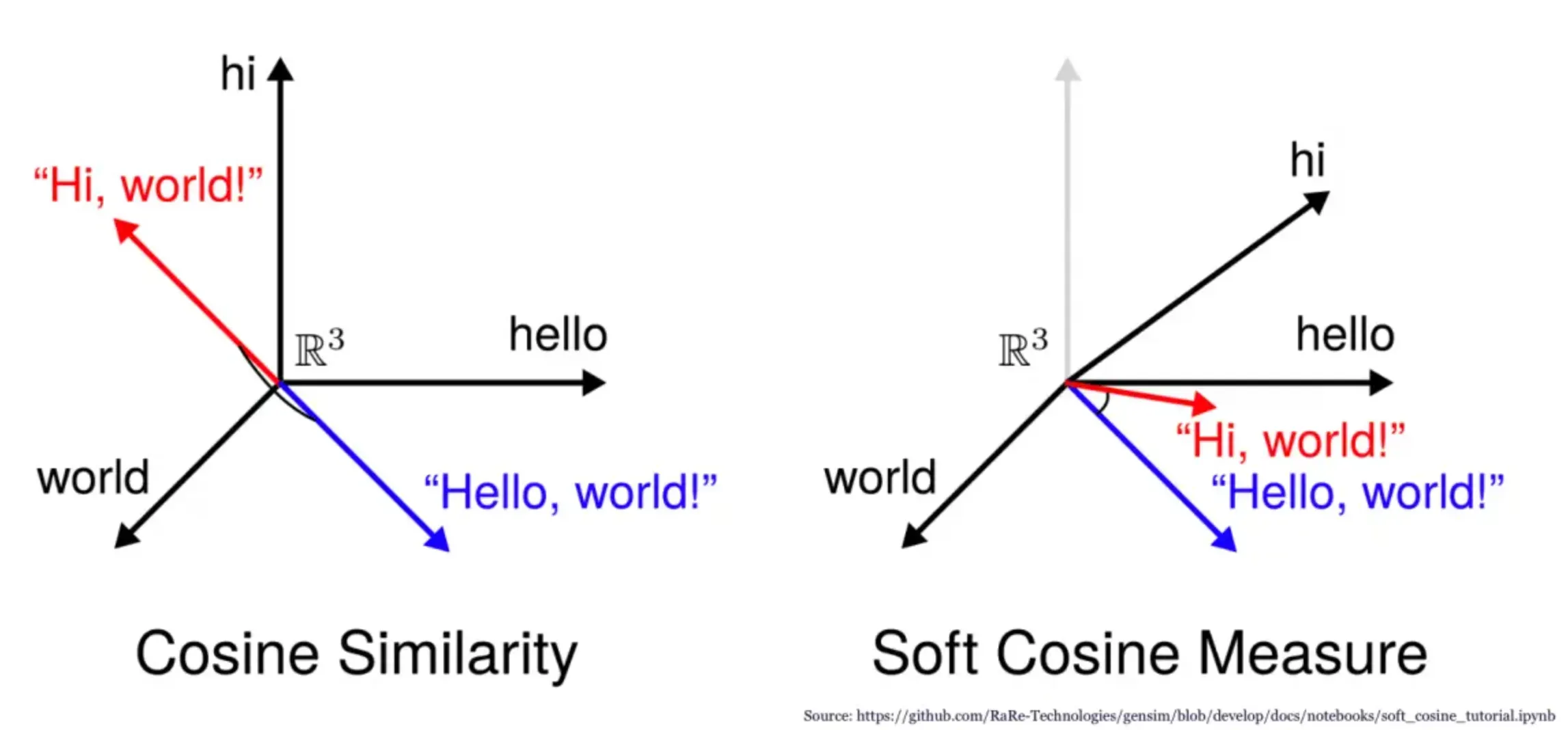
Document Matching
From plagiarism detection to search engines, matching documents is a common task. This is where Cosine Similarity sings.
Recommendation Systems
Want to suggest movies to a user? Or maybe books? Use Cosine Similarity to find items that are most similar to their preferences.
Clustering Analysis
When you deal with clusters in data, Cosine Similarity helps assess intra-cluster tightness and inter-cluster separateness.
Dimensionality Reduction
In processes like Principal Component Analysis, Cosine Similarity aids in identifying key variables.
Sentiment Analysis
Love it or hate it, sentiment analysis with NLP often takes help from Cosine Similarity to discern underlying opinions.
Who Uses Cosine Similarity?
Wondering who uses Cosine Similarity in real world? Well, it's quite popular.
Data Scientists
Data Scientists, the jugglers of the data circus, often use Cosine Similarity in their machine learning models.
SEO Specialists
In the world of Search Engine Optimization, understanding similarity between documents impacts search results. Cosine Similarity is a buddy here.
AI Engineers
Building chatbots or translators? In AI, Cosine Similarity is crucial in understanding linguistic nuances in Natural Language Processing.
Market Researchers
Comparing consumer profiles or market trends? Cosine Similarity aids market researchers in making sense of patterns and clusters.
Academic Researchers
Whether it's bioinformatics, psychology or text mining, academic researchers use Cosine Similarity to uncover hidden insights in large datasets.
Understanding Cosine Similarity with an Example
Brains love examples. Let's walk through a Cosine Similarity example to make things crystal clear.
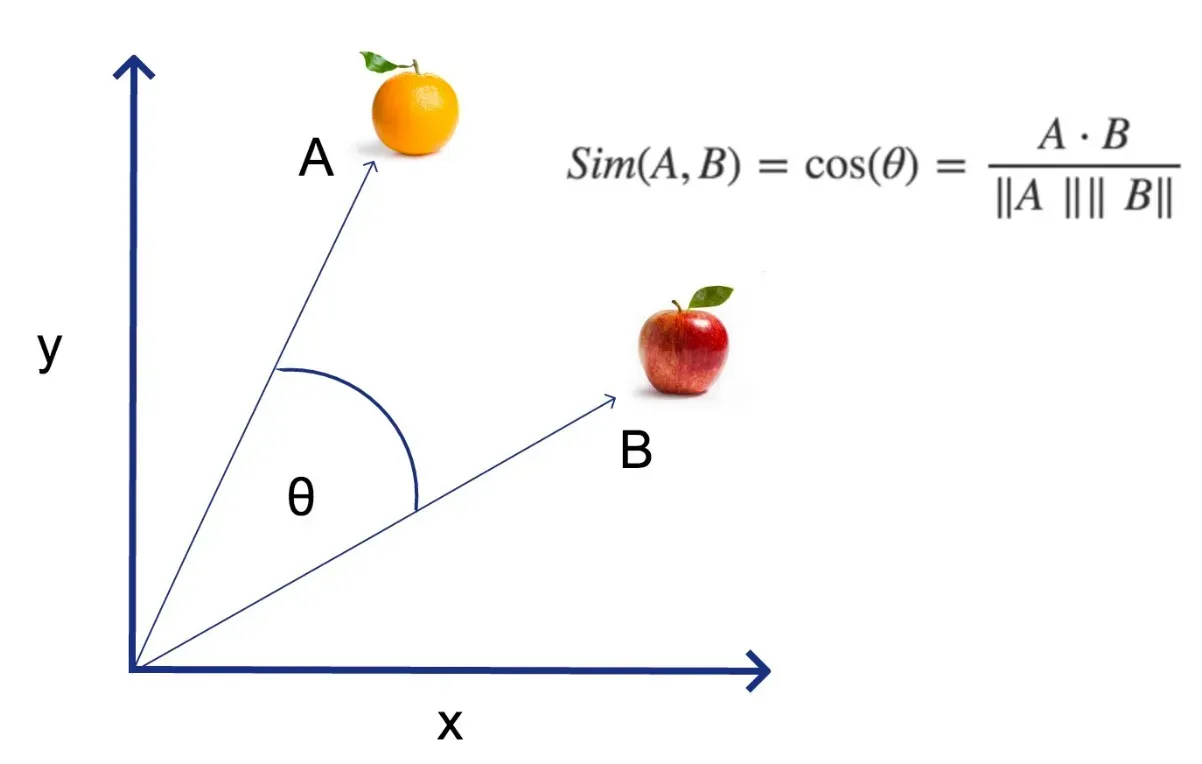
Setting Up The Problem
Let's consider movie recommendations. Assume we've a user who liked movie A and we need to recommend a similar movie B.
Feature Vector Creation
Each movie can have features like genre, director, and actors. We represent these as vectors, similar to a shopping list.
Cosine Similarity Calculation
Now, we calculate the Cosine Similarity between these movie vectors. The closer the value is to 1, the stronger our recommendation.
Analyzing the Output
If we get a high Cosine Similarity score, it means movie B is similar to A and there's a good chance the user will like it.
Rinse and Repeat
We do this for all movies in our database and, voila, we have a list of top recommendations based on Cosine Similarity.
Best Practices in Using Cosine Similarity
Just like a chisel needs the right technique to carve a masterpiece, using Cosine Similarity effectively demands knowing the best practices.
Understand Your Data
Driving blindly never ends well. Understanding your data before applying any similarity measure, Cosine Similarity included, is crucial.
Scale Your Data
Differently scaled data can tell different stories. It's good practice to scale your data to normalize it before using Cosine Similarity.
Look at the Angles
Remember that with Cosine Similarity, it's all about the angles. Similar directions imply similar entities.
Address Data Sparsity
Sparse data can be deceptive. Addressing this sparsity can improve the reliability of Cosine Similarity outputs.
Test Assumptions
Don't take things on face value. Always test assumptions and ensure that Cosine Similarity is suited for your specific use case.
Challenges in Using Cosine Similarity
Every superhero has a weakness. For Cosine Similarity, there remain a few challenges to be aware of.
Data Sparsity
Sparse data can lead to misleading results. Without sufficient non-zero dimensions, Cosine Similarity might not be the best choice.
Handling Dissimilarity
Cosine Similarity is great for measuring, well, similarity. But for dissimilarity? Not its strongest suit.
Zero Magnitude Problem
Vectors with zero magnitude can create problems in Cosine Similarity calculations, as the denominator becomes zero. Ouch!
Fallibility to Outliers
Outliers can significantly impact the direction of vectors, potentially influencing Cosine Similarity results.
Non-Interpretability
Cosine Similarity scores don't intuitively communicate similarity. A score of 0.8 doesn’t mean the items are 80% similar. It's about angles, not proportions.
Recent Trends in Cosine Similarity Application
Cosine Similarity isn't trapped in the past. Let's look at recent trends in its application.
Integration with AI and ML
Cosine Similarity is now widely integrated with AI and Machine Learning applications, enhancing the capabilities of systems interacting with human language.
Expandability with Big Data
Cosine Similarity is seeing increased use in big data. The ability to handle high-dimensional data makes it an invaluable toolkit addition.
Versatility in Fields
Cosine Similarity is venturing beyond traditional realms, finding uses in niches, from genomics to social media analytics.
Cloud Computing
With cloud-based data science platforms on the rise, tools for calculating Cosine Similarity are becoming more accessible and collaborative.
Improved Algorithms
Newer algorithms for efficient computation of Cosine Similarity, particularly for sparse and streaming data, are being developed.
Frequently Asked Questions (FAQs)
Can cosine similarity be greater than 1 or less than -1?
Nope, cosine similarity ranges between -1 and 1. Think of it like a rating for how similar two things are; it won't go outside this range.
How does text length affect cosine similarity?
The length of text doesn't matter because cosine similarity measures the angle between vectors, not their length. It's all about direction, not magnitude!
Is cosine similarity sensitive to the magnitude of values?
Nope, it isn't. Cosine similarity cares about the angle between vectors, which means it’s about the pattern of the data, not the size of the numbers.
Can cosine similarity be used with negative numbers?
Absolutely! Since it’s based on angles, even vectors with negative numbers can be compared. Negative values are just part of the directional mix.
Does cosine similarity work well with sparse data?
Yes, it does. Cosine similarity is actually pretty handy with sparse data, where it focuses on non-zero dimensions, ignoring all those zeros cluttering up the space.