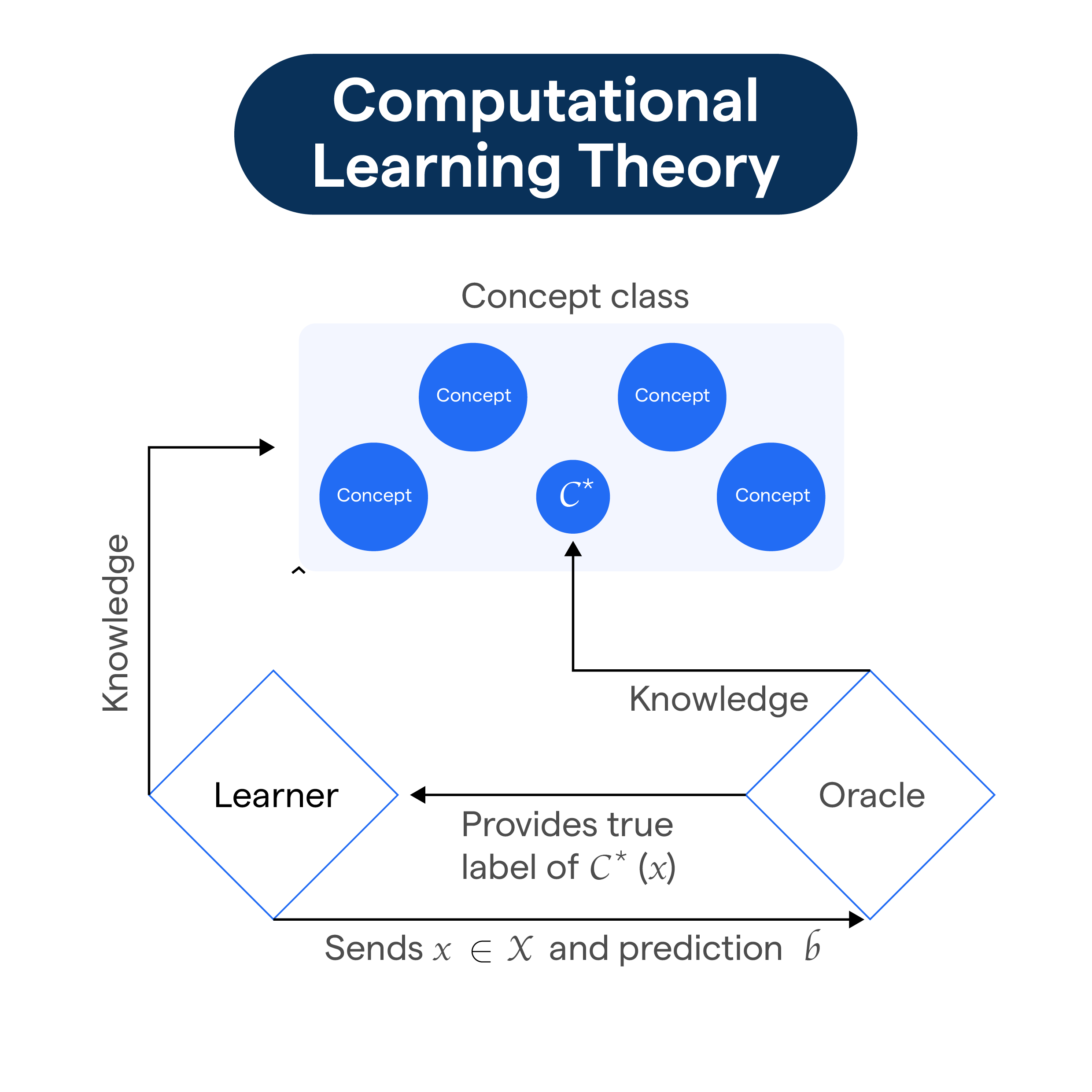
What is Computational Learning Theory?
Computational Learning Theory (CoLT) is a subfield of Artificial Intelligence that works on developing and analyzing algorithms that can learn from and make predictions based on data.
This alluring scientific field borrows from game theory, information theory, probability theory, and complexity theory to illuminate our comprehension of machine learning in a concrete and quantifiable way.
Why Computational Learning Theory?
Let's begin with a machine learning model's primary objective: To make accurate predictions.
But it can be a cryptic task to determine just how much data is sufficient to ensure these predictions' accuracy. That’s where computational learning theory shines.
The field enables us to scrutinize the machinations behind machine learning algorithms, quantifying the required data volume to improve a model’s performance.
Driving Efficiency and Innovation
The principles underpinning computational learning theory are fundamental in formulating the blueprint of machine learning algorithms. Understanding these theoretical aspects simplifies the model-building process, driving efficiency and fostering innovation.
This, in turn, forms the baseline for designing more complex and productive machine learning models, substantiating the field's significance.
Crucial in Real-world Applications
Every subdomain of technology that utilizes machine learning, from natural language processing to computer vision, health tech to fintech, stands to gain from computational learning theory. The theory accelerates machine learning deployment.
It allows researchers to tinker with machine learning algorithms, enhancing their efficiency, and making them adept at handling all kinds of data, driving better, practical real-world outcomes.
How does Computational Learning Theory work?
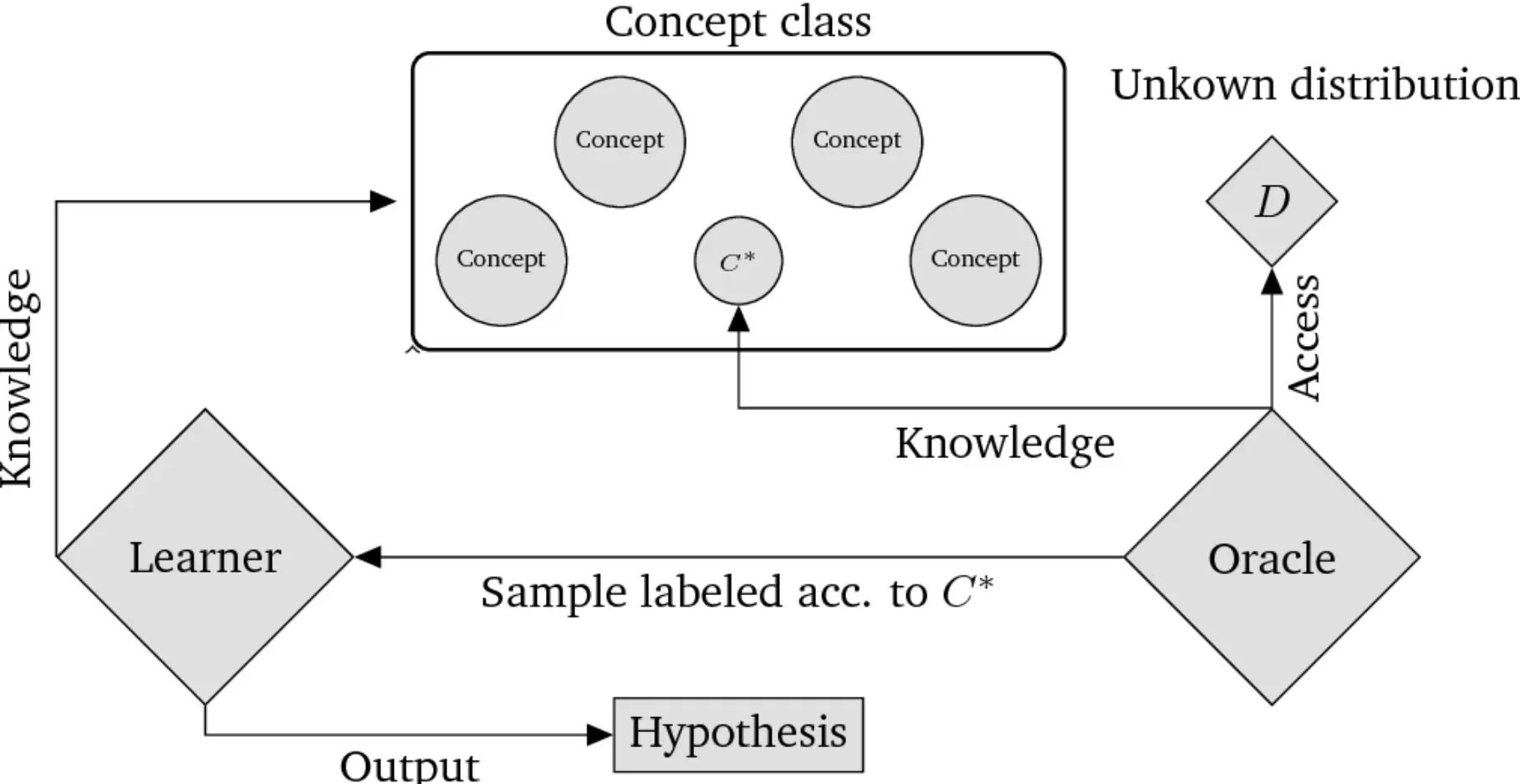
In computational theory, most learning is supervised learning. There's a concept or a task that the machine is expected to learn.
This concept is surfaced through training examples, which come in pairs. Each pair consists of an 'instance' and a 'label'. Instances are the input the machine receives, and labels are the correct output, the target.
The Learning Algorithm's Role
A learning algorithm during mandatory training makes repetitive slogs, ingesting instance-label pairs. Then, it tries to discern a generalized picture, a pattern that emerges, through the muddle of examples it parses.
That generalized picture will enable the machine to determine the labels and the right output for encounters with novel instances, instances it has never been fed before.
Samples and Hypotheses
Given infinite training examples, a machine can learn any concept or computing task, right? Wrong. That's where samples and hypotheses saunter significantly.
Every concept class has an associated number of samples beyond which there's no further improvement, no matter if the machine is provided with additional examples.
The machine arrives at this optimum through hypotheses, or prediction models, continually updating them to fit the incoming data better and dish out more precise predictions.
When is Computational Learning Theory Applied?
If an organizational task revolves around categorizing input data, computational learning theory can greatly aid the process, assisting machines in learning categories, or 'concepts,' and assigning new data inputs to these learned categories.
Predictive Modeling
The realm of predictive modeling, where the primary goal is to use sand dunes of data to divine clear murky crystal balls of future events or future trends, finds an essential ally in computational learning theory.
Resource Allocation
Allocating resources to collect vital samples or data for machine learning can be a convoluted task.
Computational learning theory, with its studied focus on the optimal number of examples required for effective learning, can aid in efficient resource allocation, ensuring the right amount of data is gathered for training.
Challenges in Operationalizing Computational Learning Theory
Computational Learning Theory, while empowering, is intricate and sophisticated. Not everyone can grasp its complexities with ease. The field requires a deep understanding of mathematics, statistics, and computer science.
Resource-Intensive
Notably, many learning algorithms that fall under the centrifuge of computational learning theory can be highly resource-intensive, requiring muscular computational horsepower. Limited resources might strain the implementation of these algorithms.
Scalability Concerns
Often, scalability can pose a challenge. Credit to the breathtaking speed at which technology evolves, colossal mounds of data accrue in the blink of an eye. In such situations, the traditional tenets of computational learning theory could falter.
The Paradox of Noise
There’s also the puzzle of noise. In a utopian vacuum, where every training example the learning algorithm confronts is perfect and accurate, learning is a breeze. But reality is far from a utopia. Data could be noisy, incomplete, inaccurate, or even contradictory.
Best Practices For Computational Learning Theory (CoLT)
These will not only help in enhancing the efficiency and effectiveness of learning algorithms but also ensure that the models developed are robust, generalizable, and capable of performing well across diverse datasets and in various conditions. Here are some detailed best practices:
Understanding the Bias-Variance Tradeoff
Trade-off Comprehension
Engaging deeply with the concept of the bias-variance tradeoff is crucial.
High bias can cause an algorithm to miss the relevant relations between features and target outputs (underfitting), whereas high variance can make the model perform well on the training data but poorly on any unseen data (overfitting).
Application
Implement techniques that balance this tradeoff effectively.
For example, increasing the model complexity might decrease bias but increase variance. Cross-validation can help estimate the model's performance on unseen data, guiding adjustments to reach an optimal balance.
Suggested Reading:
Deep Tech
Regularization
Penalizing Complexity
Regularization techniques, such as L1 and L2 regularization, add a penalty to the size of the coefficients in prediction functions to prevent the model from becoming too complex and overfitting the training data.
Practical Use
Choose a regularization method based on the problem at hand. L1 regularization can lead to a sparse model where irrelevant features are assigned a weight of zero, useful for feature selection.
L2 regularization generally results in better prediction accuracy because it keeps all features but penalizes the weights of less important features.
Validation Techniques
Cross-validation
Implement cross-validation, especially k-fold cross-validation, to better estimate the model's ability to generalize to unseen data.
This involves dividing your dataset into k smaller sets (or 'folds'), using k-1 of them for training the model and the remaining set for testing, and repeating this process k times with each fold used exactly once as the test set.
Validation Set
Besides cross-validation, using a validation set (separate from the testing set) during the training process can help tune model parameters without overfitting the test set. This is crucial for assessing how well the model has generalized.
Algorithm Selection and Complexity
Right Algorithm for the Right Problem
Not every learning algorithm is suitable for every type of problem. It's essential to understand the strengths and weaknesses of different algorithms and select the one that aligns with the specifics of your task and data.
Consider Complexity
Be cautious of the algorithm's complexity in relation to your available computational resources.
More complex algorithms, such as deep learning models, may provide higher accuracy but also require significantly more computational power and data.
Staying Updated and Mitigating Overfitting
Continuous Learning
The field of computational learning theory is rapidly evolving. Staying updated with the latest research findings, algorithms, and techniques is vital for applying the most effective and efficient learning methods.
Strategies Against Overfitting
Apart from regularization and cross-validation, consider other strategies to prevent overfitting, such as pruning decision trees or using dropout in neural networks.
Ensemble methods like bagging and boosting can also help by aggregating the predictions of several models to improve robustness and accuracy.
Frequently Asked Questions (FAQs)
What is the Core Focus of Computational Learning Theory?
Computational Learning Theory focuses on designing efficient algorithms that can 'learn' from data and make theoretical predictions about their performance.
How Does Computational Learning Theory Contribute to Machine Learning?
It provides the underpinnings for machine learning by quantifying the 'learnability' of tasks and guiding algorithm design and implementation.
What's the Significance of "PAC Learning" in Computational Learning Theory?
"Probably Approximately Correct" (PAC) Learning provides a formalized framework to understand and quantify the performance of learning algorithms.
Do Computational Learning Theory Concepts Impact AI Development?
Yes, the principles and results of Computational Learning Theory guide the development of AI systems that adapt and learn from their environment.
Does Computational Learning Theory Offer Insights into Human Learning?
While not its primary focus, this theory does offer interesting parallels and can spur discussions around human learning processes and brain computation.