What are Autoregressive Models?
At their core, autoregressive models are a type of statistical model used for forecasting in time series data. Imagine you could predict tomorrow’s weather just by analyzing the patterns of the past.
Definition
An autoregressive model predicts future behavior based on past behavior. It's like saying, "If I know my past steps, I can guess where my next step will be."
Core Components
The heart of these models lies in their reliance on past values. Think of them as the self-reflective thinkers of the statistical world.
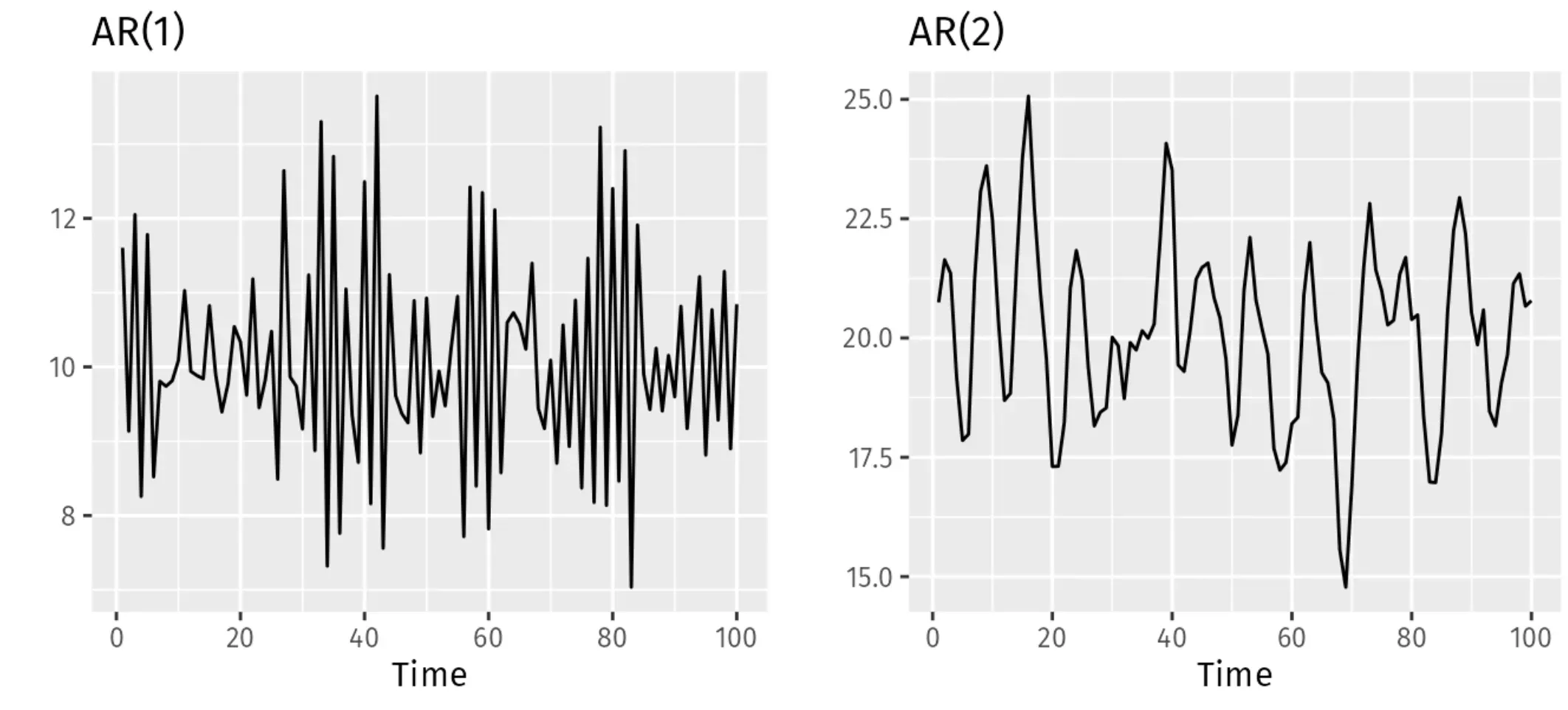
The AR(p) Model
This refers to the autoregressive model of order p, where 'p' indicates the number of lagged observations in the model. It’s like deciding how many chapters back you need to read to understand the story's current arc.
Coefficients
These are the weights the model assigns to the previous terms. It tells us how important past values are for predicting the future.
Stationarity Requirement
For autoregressive models to work their magic, the time series data must be stationary. This means its properties do not depend on the time at which the series is observed.
Why Use Autoregressive Models?
Now, you might wonder, "Why bother with these models?" Well, they pack some neat advantages in their statistical toolbox.
Simplicity
One of the beauties of autoregressive models is their straightforwardness. They offer a relatively simple way to forecast based on historical data.
Efficiency
When the conditions are right, these models can be incredibly efficient in forecasting, especially for short-term predictions.
Flexibility
Autoregressive models can be adapted and extended into more complex models, making them versatile tools in a forecaster's arsenal.
Predictive Power
Under certain conditions, the predictive accuracy of AR models can rival or even surpass that of more complex models.
Understanding Data
They help in understanding the dynamics of the time series, making it easier to identify trends, cycles, and seasonality.
How Do Autoregressive Models Work?
Diving deeper, let's peel back how these models take historical data and turn it into future insights.
The Basic Equation
The heart of an autoregressive model is its equation, where the future value is a sum of past values multiplied by their respective coefficients, plus some error term.
Lagged Variables
These are the previous time points used to predict the future. In AR models, your predictors are your own past selves.
Estimation
Typically, coefficients are estimated using methods such as the Maximum Likelihood Estimation or the Yule-Walker equations.
Model Fitting
This involves selecting the appropriate number of lags (p) and ensuring the model adequately captures the data dynamics without overfitting.
Forecasting
Once fitted, the model can be used to make forecasts. The further ahead you predict, the less accurate these forecasts tend to be, much like trying to forecast the weather months in advance.
When to Use Autoregressive Models
Knowing when to deploy these models can be as crucial as understanding how they work.
Short-Term Forecasting
Autoregressive models shine brightest in the short-term forecasting arena, where past data strongly indicates future trends.
Stationary Time Series Data
These models are your go-to when dealing with data that has constant mean and variance over time.
Analyzing Financial Markets
From stock prices to exchange rates, AR models are invaluable tools for analyzing and forecasting financial time series.
Signal Processing
They are also used in signal processing to extract patterns from noise, helping in everything from telecommunications to seismology.
Climate Modeling
Predicting weather patterns and climate changes often relies on autoregressive models for short-term forecasts.
Challenges in Using Autoregressive Models
As powerful as they are, autoregressive models are not without their limitations and challenges.
Stationarity Issue
The biggest hiccup? The data must be stationary, which is often not the case in real-world scenarios.
Choosing the Right Order (p)
Determining the optimal number of lagged variables (p) can be more art than science, requiring expertise and experimentation.
Overfitting
With too many lag variables, there's a risk of overfitting, where the model performs well on historical data but poorly on future data.
Underlying Assumptions
The model assumes a linear relationship between past and future values, which might not always hold true.
Impact of External Factors
Autoregressive models focus on internal dynamics and might overlook the impact of external shocks or events on the series.
Trends in Autoregressive Modeling
The field of autoregressive modeling is not static; it evolves as new theories, techniques, and computational methods emerge.
Integration with Machine Learning
Combining AR models with machine learning techniques offers powerful new ways to analyze and forecast complex time series data.
Increased Computational Power
Advancements in computational capabilities are enabling researchers to fit more complex models over larger datasets, opening new frontiers in forecasting.
Multivariate Extensions
Moving beyond single-variable models, the focus is increasingly on multivariate versions that can handle complex interdependencies between multiple series.
Real-time Forecasting
The push towards real-time data analysis is shaping how autoregressive models are being developed and deployed, making forecasts timelier and more relevant.
Customization and Personalization
As the demand for tailor-made solutions grows, autoregressive models are being customized to suit specific industry needs and challenges.
Best Practices in Autoregressive Modeling
To harness the full potential of autoregressive models, keep these best practices in mind.
Preprocessing
Ensuring data is stationary and appropriately transformed before model fitting is crucial. Techniques like differencing or log transformations can be useful.
Model Selection
Start with simpler models and gradually increase complexity as needed. It’s often more effective than starting with a very complex model.
Validation
Use hold-out validation sets to evaluate model performance. This helps in assessing how well your model will generalize to unseen data.
Regularization
Incorporate penalization methods like Lasso or Ridge Regression to prevent overfitting, especially when dealing with high-order models.
Iterative Refinement
Model building is an iterative process. Continuously refine your model based on new data and feedback to ensure it remains relevant and accurate.
Tackling Common Misconceptions
Finally, let's clear up some common misconceptions about autoregressive models.
Predictive Limitations
AR models are not a crystal ball. Their predictive power diminishes as the forecast horizon extends, especially in volatile or non-stationary contexts.
Model Complexity
More complex models are not necessarily better. A simpler model with robust validation often outperforms a complex model with poor validation.
Exclusive Use
Autoregressive models are not the be-all and end-all of time series forecasting. They are part of a broader toolkit that includes moving average models, exponential smoothing, and more.
Data Sufficiency
Having a large amount of data does not guarantee better forecasts. The quality of data and the relevance of the lagged variables play a crucial role.
Stationarity Transformation
Transforming non-stationary data into stationary form does not always make it suitable for AR modeling. The transformation must preserve the essence of the data dynamics.
Frequently Asked Questions (FAQs)
What is the Core Principle of Autoregressive Models?
Autoregressive Models are based on the idea that current observations in a time series are correlated with previous observations, allowing for predictions based on historical data.
How Are Lags Incorporated in Autoregressive Models?
Lags, or previous observations, are used as input variables in the Autoregressive model, where the number of lags forms the order of the model.
Are Autoregressive Models Suitable for Non-stationary Data?
Generally, Autoregressive Models require data to be stationary. However, with differencing or transformations, they can accommodate non-stationary data.
How do Autoregressive Models Handle Seasonal Variations?
Seasonal variations can be managed using the Seasonal Autoregressive (SAR) model, allowing the model to account for regular patterns in cycle length.
What are the Real-life Applications of Autoregressive Models?
Autoregressive Models are widely used in economic forecasting, stock price prediction, weather forecasting, and anything related to time-series data.