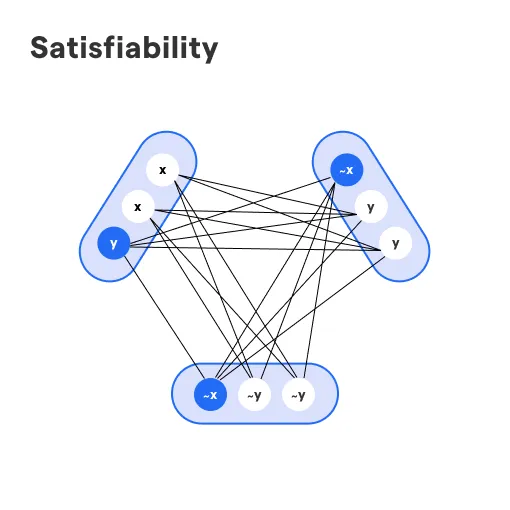
What is Satisfiability?
Satisfiability refers to the property of a formula being true in some interpretation. In other words, a formula is considered satisfiable if there exists a model that makes the formula true.
Conversely, a formula is unsatisfiable if none of the models satisfy the formula. Validity, on the other hand, refers to a formula being true in all interpretations. If all models satisfy a formula, it is considered valid.
Why is Satisfiability important?
Satisfiability is important for several reasons. Here are five key reasons:
Problem-Solving
Satisfiability is a fundamental concept in computer science and mathematics. It is used as a tool to solve a wide range of problems, including optimization, planning, scheduling, and decision-making.
By modeling these problems as Boolean formulas and checking their satisfiability, we can find solutions or determine if a solution exists.
Verification and Validation
Satisfiability plays a crucial role in verifying the correctness of digital systems. The ability to check the satisfiability of a logical formula allows us to determine if a system design or specification satisfies certain properties or constraints.
This is particularly important in safety-critical domains like aerospace, automotive, and healthcare where rigorous validation is essential.
Complexity and Algorithms
Satisfiability is a well-studied problem in computer science, mainly because it has significant implications for the field of computational complexity.
The study of satisfiability has led to the development of efficient algorithms, heuristics, and techniques that are applicable to a wide range of other computational problems.
Artificial Intelligence
Satisfiability is closely related to the field of artificial intelligence, especially in the areas of automated reasoning and knowledge representation. Problems like logical inference, planning, and constraint satisfaction can often be reduced to the problem of checking satisfiability.
Satisfiability solvers are used in various AI applications, including expert systems, natural language processing, and robotics.
Hardware and Software Verification
In the context of hardware and software design, satisfiability is crucial for formal verification. Formal methods use mathematical models and logical reasoning to analyze and prove the correctness of designs.
Satisfiability solvers are employed to check if hardware or software models satisfy specific properties or to find counterexamples that demonstrate bugs or design flaws.
Where is Satisfiability applied?
Satisfiability finds applications in numerous domains. In hardware design, it is used to check the equivalence of two designs and to verify the functional correctness of a design through test generation.
In software analysis, Satisfiability helps in program verification, bug detection, and interpreting program behavior.
It also plays a pivotal role in cryptography, where it is used to analyze the security of cryptographic protocols.
When is Satisfiability used?
Satisfiability is used in situations where the truth of a formula needs to be established. It is employed when checking the consistency of systems, verifying the correctness of designs, or exploring the feasibility of solutions. Satisfiability is also utilized when analyzing puzzles, logical problems, and mathematical theorems.
How does Satisfiability work?
Certainly, here is a brief explanation of how Satisfiability works:
Boolean Formulas

Satisfiability is a problem in computational complexity theory that involves checking whether the variables in a Boolean formula can be assigned in a way that makes the formula evaluate true.
A Boolean formula is a statement that can be either true or false. It is composed of variables, logical operators (such as AND, OR, NOT), and parentheses.
For example, the formula (A AND B) OR NOT C is a Boolean formula with the variables A, B, and C.
Satisfiability Problem
The Satisfiability problem asks whether it's possible to find an assignment of values (TRUE or FALSE) to the variables in a formula that makes the formula true.
The problem can be stated as follows: given a Boolean formula, find an assignment of values to its variables that make the formula evaluate to true.
Decision Procedure
To check the satisfiability of a Boolean formula, one can use a decision procedure, which is an algorithm that determines whether the formula is satisfiable or not.
One such decision procedure is the Davis-Putnam-Logemann-Loveland (DPLL) algorithm.
Backtracking
The DPLL algorithm uses a backtracking search technique to explore the space of possible assignments to the variables in a formula. At each step, the algorithm chooses a variable to assign a value (TRUE or FALSE) and checks whether the resulting formula is satisfiable.
If the formula is satisfiable, then the algorithm terminates, and it returns the assignment of values to the variables. If the formula is not satisfiable, then the algorithm backtracks and tries a different value for the chosen variable or chooses a different variable and tries again.
Complexity Analysis
The satisfiability problem is NP-complete, meaning that it's unlikely that there exists an efficient algorithm that can solve all instances of the problem.
Despite this, researchers have developed many efficient algorithms and heuristics that can solve many practical instances of the problem in a reasonable time.
Types of Satisfiability Problems
Satisfiability problems can be categorized into different types.
Boolean Satisfiability Problem (SAT)
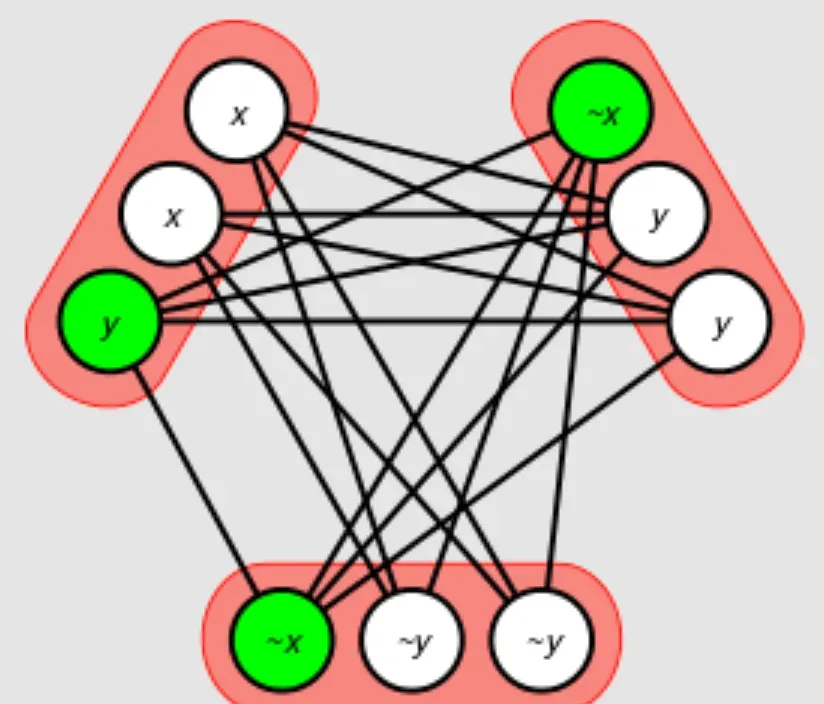
The Boolean Satisfiability Problem, commonly referred to as SAT, is one of the most well-known and studied satisfiability problems.
It involves determining if there exists an assignment of truth values (TRUE or FALSE) to variables in a Boolean formula such that the formula evaluates to true.
SAT is NP-complete, meaning that it is computationally challenging to find a solution in the general case.
Satisfiability Modulo Theories (SMT)
Satisfiability Modulo Theories refers to the problem of determining the satisfiability of a formula that combines Boolean variables with variables and constraints from different theories, such as arithmetic, arrays, bitwise operations, or strings.
SMT solvers are powerful tools for solving complex problems in diverse domains that involve multiple theories.
Quantified Boolean Formula (QBF)
Quantified Boolean Formula extends the SAT problem by allowing the use of quantifiers (∃ for existentially quantified variables and ∀ for universally quantified variables).
QBF asks whether a given quantified Boolean formula is true for all possible assignments of truth values to its variables. Solving QBF is more complex than SAT, and it is a PSPACE-complete problem.
Propositional Satisfiability with Cardinality Constraints (SAT+C)
In SAT+C, additional constraints are added to traditional Boolean formulas to express cardinality constraints, such as specifying a certain number of variables that must be true or false.
SAT+C can capture problems like maximum satisfiability, where one seeks to maximize the number of satisfied clauses in a Boolean formula under certain constraints.
Satisfiability with Constraints (CSP)
Constraint Satisfaction Problems involve finding assignments of variables satisfying specified constraints.
Unlike SAT problems, where only Boolean variables are used, CSP deals with variables that can have different domains and constraints defined over them.
CSP finds applications in areas such as scheduling, planning, and resource allocation.
Challenges in Satisfiability
Here are the challenges associated with satisfiability problems:
Computational Complexity
Satisfiability problems are often difficult to solve efficiently. Many of them are classified as NP-complete or PSPACE-complete, indicating that finding a general solution algorithm with polynomial time complexity is unlikely.
Problem Size and Scaling
Satisfiability problems can quickly become large and complex, making it challenging to solve real-world instances with thousands or millions of variables and clauses.
The exponential nature of the problem leads to a massive search space, which can be computationally intractable.
Expressiveness and Modeling
Accurately representing real-world problems as satisfiability problems can be challenging. Choosing the right model and encoding the problem's constraints accurately is crucial for efficient solving.
If the model does not capture all the relevant aspects of the problem, the solution approach may not be effective.
Trade-offs in Efficiency and Completeness
Satisfiability solvers often face a trade-off between efficiency and completeness. Complete solvers aim to find an optimal solution or prove unsatisfiability but may require more time and resources.
Heuristic or incomplete solvers may provide faster results but cannot guarantee optimality or unsatisfiability proof.
Applications of the SAT Problem: The Real-World Influence
The SAT problem, with its propositions and logical puzzles, is not confined to a computational theory. It has substantial real-world applications, influencing a variety of sectors from technology to transportation.
Hardware and Software Verification
The SAT problem plays a crucial role in the field of computer hardware and software verification.
By translating design specifics into Boolean logic, which can then be solved by SAT, engineers can evaluate the validity and performance of a given design.
Systems ranging from digital circuits to complex algorithms can be verified for inconsistencies, bugs, and failures by applying various SAT-solving tools. The result is a safer, more reliable technology infrastructure.
Artificial Intelligence (AI)

In the world of AI, SAT algorithms are used in automated reasoning - the ability of AI systems to understand and solve complex problems.
Whether it's predicting potential scenarios or making strategic decisions, SAT offers a way to explore various outcomes based on a set of given variables.
This form of predictive modeling is fundamental to modern AI applications like autonomous vehicles, conversational AI, and robot navigation.
Planning and Scheduling
Another practical application of SAT falls in planning and scheduling problems, commonly found in domains like project management, transportation, or manufacturing.
Scheduling issues often revolve around assigning resources optimally under a set of constraints. By translating these problems into SAT problems, we can leverage SAT solvers to find optimal solutions.
These techniques have been incorporated into a range of industries,, like air traffic control, production line management, and logistics planning.
Cryptography
In cryptography, SAT problems are utilized to test the security of existing systems.
Given the complexity of SAT, an encrypted system deemed as hard to solve as a satisfiability problem is considered secure from most brute-force attacks.
Subsequently, any inconsistencies or vulnerabilities in the system can be systematically uncovered by treating them as a SAT problem.
Biology and Medicine
The SAT problem has found an unexpected playground in the life sciences. Biological systems often present as a series of decisions made under certain conditions - just like a SAT problem.
From genetic research looking at gene expression and regulation to medical diagnostics that employ algorithm-based diagnoses - SAT transforms complex biological data into logically solvable problems.
Frequently Asked Questions (FAQs)
What is the SAT problem?
The SAT problem is about determining if there exists an assignment of truth values to variables in a Boolean formula such that the formula evaluates to true.
What is the difference between SAT and SMT?
SAT deals with Boolean variables only, while SMT extends SAT to include variables and constraints from different theories like arithmetic, arrays, bit operations, or strings.
Are satisfiability problems always difficult to solve?
Yes, many satisfiability problems are computationally challenging. They are often classified as NP-complete or PSPACE-complete, indicating their inherent complexity.
How does problem size impact satisfiability solving?
As the problem size grows, satisfying large and complex formulas becomes more challenging due to the exponential growth of the search space, leading to longer computation times and resource requirements.
What are some applications of satisfiability solving?
Satisfiability solving has applications in various domains like software verification, hardware design, planning, scheduling, and artificial intelligence, providing solutions to constraint satisfaction problems in diverse fields.