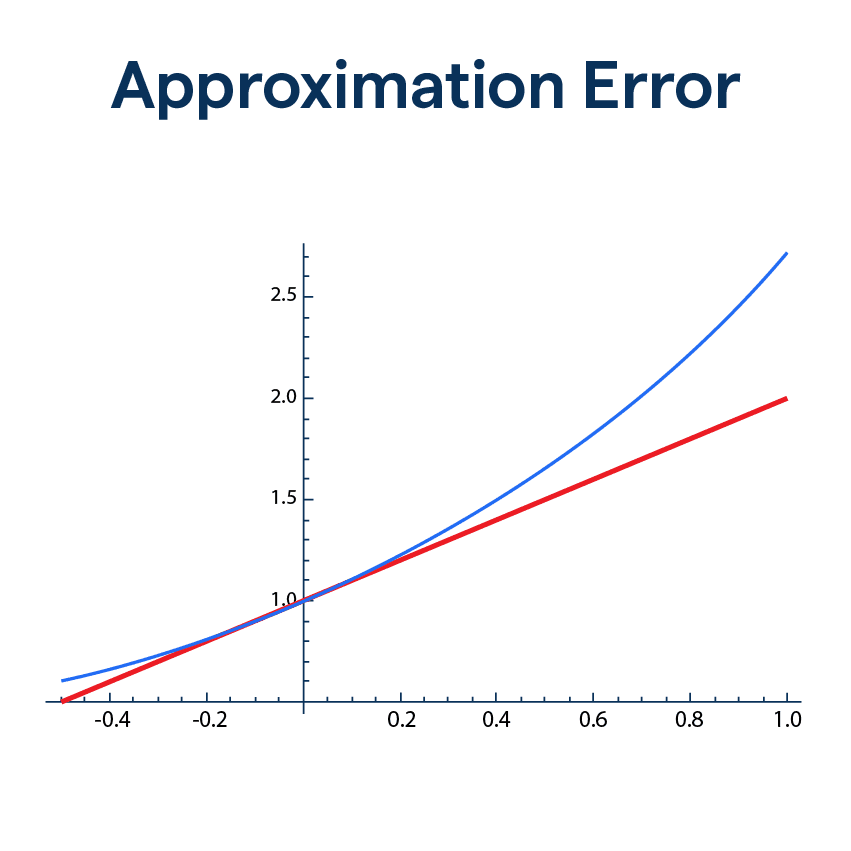
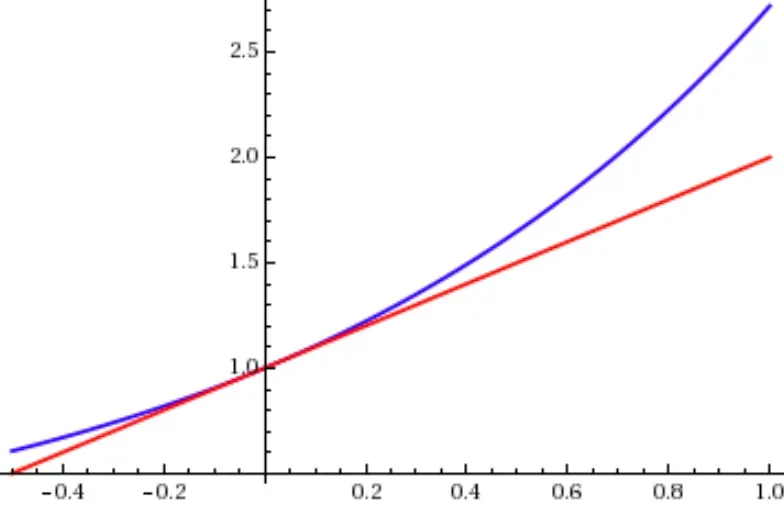
What is Approximation Error?
Here's the 101 on Approximation Error - it's the difference between the true value (like your doorstep) and the estimated value (where your GPS led you). It's a measure of how "off" we are in our computations or measurements. It's like a GPS has inherent error – no device is perfect, right?
Types of Approximations
Two main types may show up in your maths rendezvous: truncation and rounding errors.
- Truncation error occurs when we simplify a math function by chopping off (or truncating) the less significant parts, leading to an approximation.
- Rounding errors spring up when we round off numerical values to make calculations simpler – kind of like saying, "I'm five and a half" instead of "I'm five years, six months, and thirteen days old."
Finding Approximation Error
Calculating the approximation error is pretty straightforward – just subtract the approximate value from the exact one. In mathematical lingo, the absolute error is the absolute value of this difference.
Practical Importance
In the real world, knowing the approximation error has some serious perks. It can tell you how accurate your GPS device is, or how close your calculation is to the exact, so you're never left wondering if your result is "good enough"!
Handling Approximation Error
Several factors can influence your approximation error, from the precision of your tools or methods to inherent limitations in your data or algorithms. It's like trying to cut a cake into perfect pieces using a butter knife – definitely not the right tool for precision!
Strategies
Successful handling of approximation error involves minimizing it as best as possible. Choosing more precise tools, using more sophisticated algorithms, and carefully validating your data can go a long way to cut down approximation errors.
Dealing with Errors in Different Mathematical Operations
Each mathematical operation is uniquely susceptible to certain types of errors. For instance, subtraction might cause catastrophic cancellation, where most significant digits are lost, ballooning the approximation error.
Computational Considerations
From a computer science perspective, algorithms are often built considering the fine balance between computational effort and approximation error. The goal is to keep the error within acceptable bounds without overtaxing the computational resources.
Real-world Examples of Approximation Error
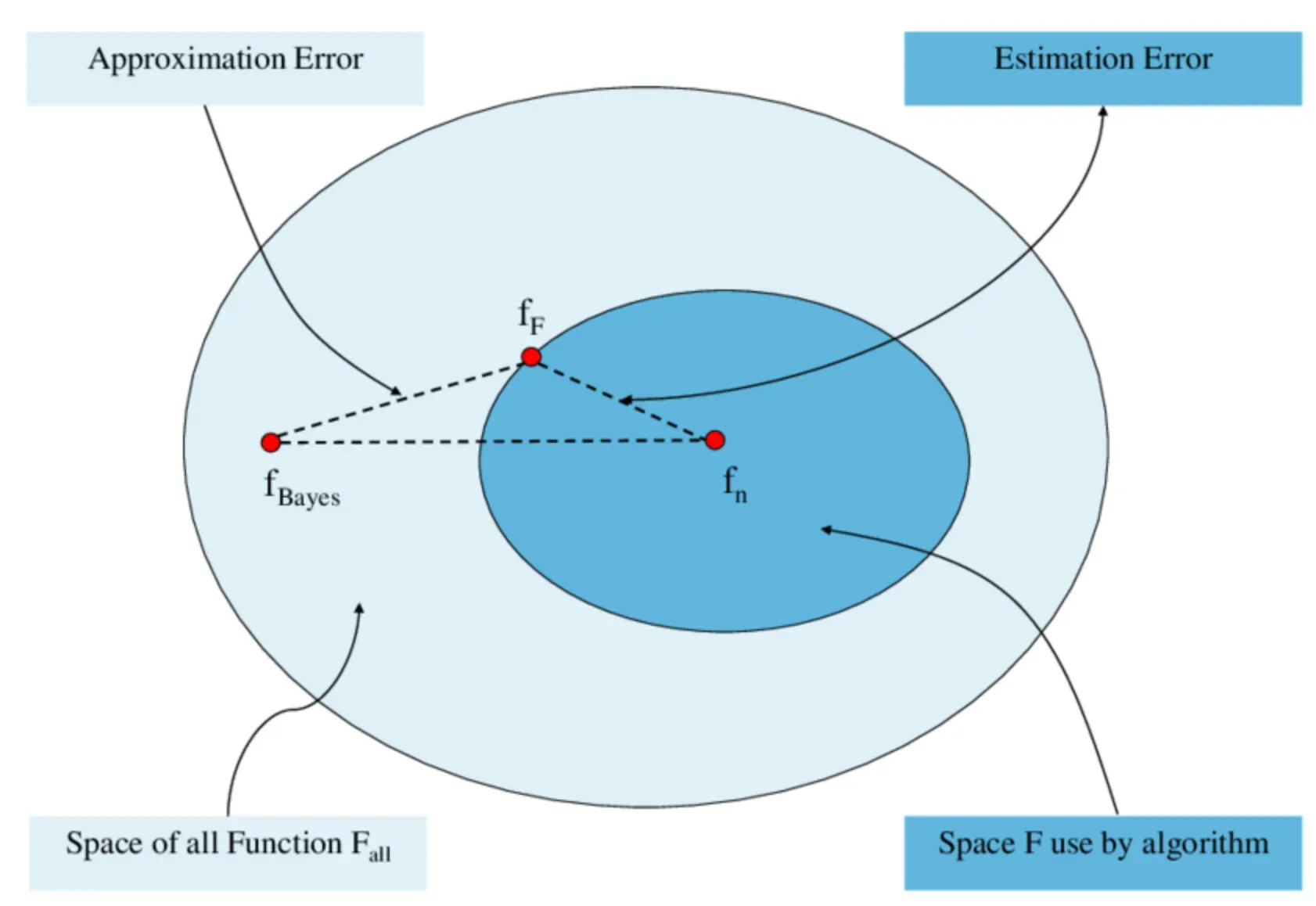
Science and Engineering
In scientific experiments or engineering calculations, approximation error is like a ghost lurking under the bed. It can subtly but significantly impact results or designs.
GPS
Even sophisticated devices like GPS systems aren't immune to approximation error, which affects the accuracy of location data. Like being dropped off some houses away from your friend's place when you're unfamiliar with the area!
Weather Predictions
This one hits close to home. Approximation errors crop up in our everyday weather predictions, leading to those uncannily wrong forecasts.
In Machine Learning
ML algorithms often deal with approximation errors, especially in regression tasks, where the challenge is to predict continuous values as accurately as possible.
How to Interpret Approximation Error?
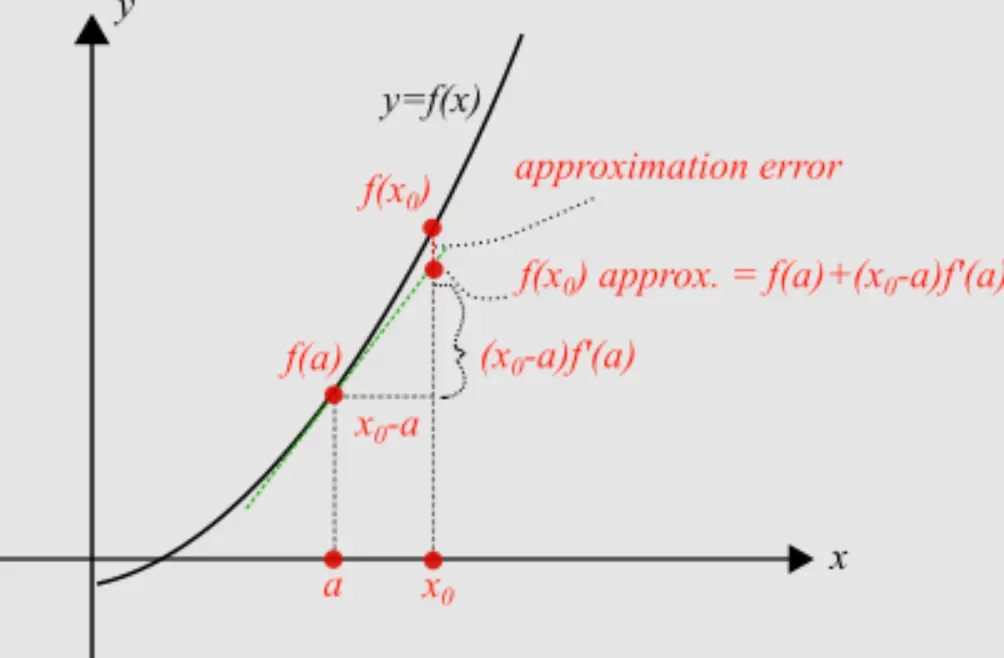
Context Matters
It's not always about the smallest error. The context matters when interpreting approximation errors. In some cases, a larger approximation error might be acceptable, and in others, even a tiny error might be significant.
For example, a small error in manufacturing a microchip can be catastrophic, while the same might not hold true for the dimensions of a football field!
The Role of Units
One of the key aspects to consider when interpreting approximation error is the units being used. Measurements in centimeters might tolerate a higher approximation error than the same measurements in millimeters!
Comparing Approximation Errors
When you're comparing different methods or tools using approximation error, ensure they're compared on the same scale or data for a fair evaluation.
Balancing Accuracy and Complexity
Finally, understanding approximation error is about striking a balance: higher accuracy often comes at the cost of increased complexity or computational effort.
Frequently Asked Questions (FAQs)
What is an Approximation Error?
Approximation error is the quantitative measure of the difference between a computed or measured value and the actual or true value.
What causes Approximation Error?
Approximation error can arise from a variety of factors, including the precision of the tools or instruments used, the numerical methods or algorithms adopted, and the inherent limitations or uncertainty in the data.
Why is Approximation Error important?
The importance of approximation error lies in its ability to indicate the accuracy of a result or prediction. It can help scientists, engineers, or data analysts to understand the reliability of their findings or models.
How to minimize Approximation Error?
Minimizing approximation error involves techniques like using more precise tools or instruments, choosing more accurate algorithms or methods, and ensuring high-quality data.
Does every calculation or measurement have an Approximation Error?
Yes, practically every calculation or measurement will have some approximation error. It's due to the inherent limitations in our tools, methods, and numerical representations. The key lies in managing and understanding this error.