What is Zipf's Law?
Zipf's Law states that in a wide range of natural systems, the frequency of an item is inversely proportional to its rank in the frequency table.
Essentially, this means that the most frequent word in a language will occur approximately twice as often as the second most frequent word, three times as often as the third most frequent word, and so on.
History of Zipf's Law
The law was originally noted by George Kingsley Zipf, an American linguist and philologist, during his investigations on word use in natural languages.
He proposed it not just as a statistical observation but as a law of nature.
Concept and Visualization
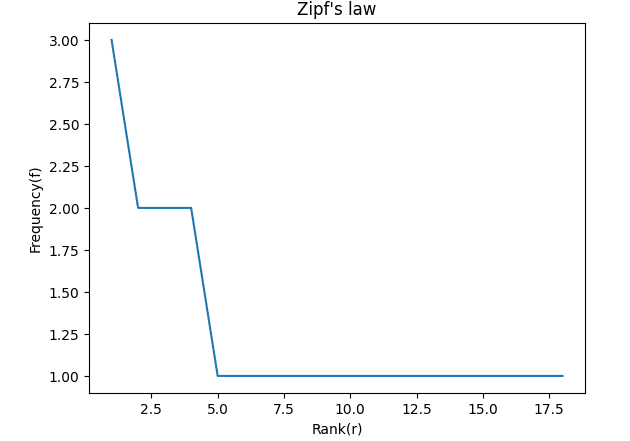
Zipf’s law can be visualised on a log-log graph, with the axes being log (rank order) and log (frequency). The resulting line on the graph has a slope of -1, which signifies that it follows Zipf's Law.
General Formula
The frequency of any word in a text corpus is approximately equal to the reciprocal of its rank times a constant. The general formula is f = C/r, where f is the frequency, r is the rank, and C is a constant.
Applications of Zipf’s Law
Next, we will look into where Zipf's Law is applied.
- Linguistics: In Linguistics, Zipf's Law can predict the distribution of word frequencies. It's a crucial tool in natural language processing (NLP) and has applications in keyword extraction or text mining.
- Sociology: Some sociologists have used Zipf's law to represent the distribution of wealth in society or to describe city populations' distribution or organisational structures.
- Internet and Web Analytics: In web analytics, the distribution of website visitors often follows Zipf’s law. The most-visited site gets the lion's share of traffic, and the rest taper off in a pattern that follows the law.
- City Planning and Urban Growth: Zipf's Law is used to understand city sizes, determining that a few cities are large while many small cities are proportional to their rank.
Interpretations of Zipf's Law
In this segment, we will delve into several ways Zipf's Law is interpreted and understood.
The Principle of Least Effort

Zipf himself proposed that his law indicates a sort of natural economy, an equivalent of the Principle of Least Effort, which suggests that patterns in language minimise the overall effort of the speaker and hearer.
Randomness and Structure
Some argue that Zipf's law reveals an interaction between underlying structures in physical or social systems and random behaviour, reflecting chaos and order's delicate balance.
Miracle or Artifact?
While some proponents consider Zipf's Law as a profound insight into complexity's nature, sceptics perceive it to be an artefact of the methodologies used in data analysis.
Information Theory
In Information theory, Zipf's law connects to entropy, which measures randomness or disorder within a set of data. It provides insight into information compression, coding, and representation.
Limitations and Criticisms of Zipf's Law
Despite its allure, Zipf's law has been challenged on several fronts, which we will outline here.
- Not Universal: Critics argue that while Zipf's law appears to hold in many contexts, it isn't universal. Certain datasets do not follow the distribution predicted by Zipf's Law.
- Ignoring the Meanings of Words: A criticism of Zipf's law in linguistics is that it only accounts for word frequency and neglects the context or meaning of words.
- Variations in Rank-Frequency Relationship: Some research has found that the rank-frequency relationship can significantly vary depending on the text's length and language, indicating more complexity than Zipf's Law might suggest.
- Lack of Theoretical Explanation: Another criticism is that Zipf's Law does not offer a theoretical explanation – it merely observes and describes a phenomenon but fails to provide a mechanistic model that explains why the phenomenon occurs.
Zipf's Law in Popular Culture
Let's examine how Zipf's Law has been embraced and referenced in popular culture.
Algorithms and Data Structures
Zipf’s law is often used in computer science in developing algorithms and databases to demonstrate the distribution of elements.
Search Engines
Search engines and text indexing technologies often take advantage of Zipf's Law. Inverted indices that store the occurrences of words in documents are based on the principle of this law.
Literature and Film
References to Zipf’s law occur in literature and film, sometimes as plot devices or metaphors for societal order or chaos.
Digital Humanities
In digital humanities, scholars use Zipf's law to analyse the usage of words and phrases in vast libraries of texts, facilitating large-scale literary analysis.
Frequently Asked Questions (FAQs)
How does Zipf's Law apply to SEO?
Zipf's Law helps identify the most frequent keywords, enabling optimization strategies to improve search engine rankings.
Why is word frequency distribution important in SEO?
Understanding word frequency distribution helps prioritise keywords for content optimisation and target high-ranking search queries.
Can Zipf's Law be used for keyword research?
Yes, Zipf's Law can help identify common keywords in a niche, allowing for better keyword targeting and improved SEO performance.
How can I optimise my content using Zipf's Law?
Strategically incorporating high-frequency keywords in headings, meta tags, and content bodies can enhance SEO and improve rankings.
What is the role of long-tail keywords in relation to Zipf's Law?
Long tail keywords, combined with Zipf's Law, can attract specific and less competitive search traffic, boosting visibility and relevance for certain niches.