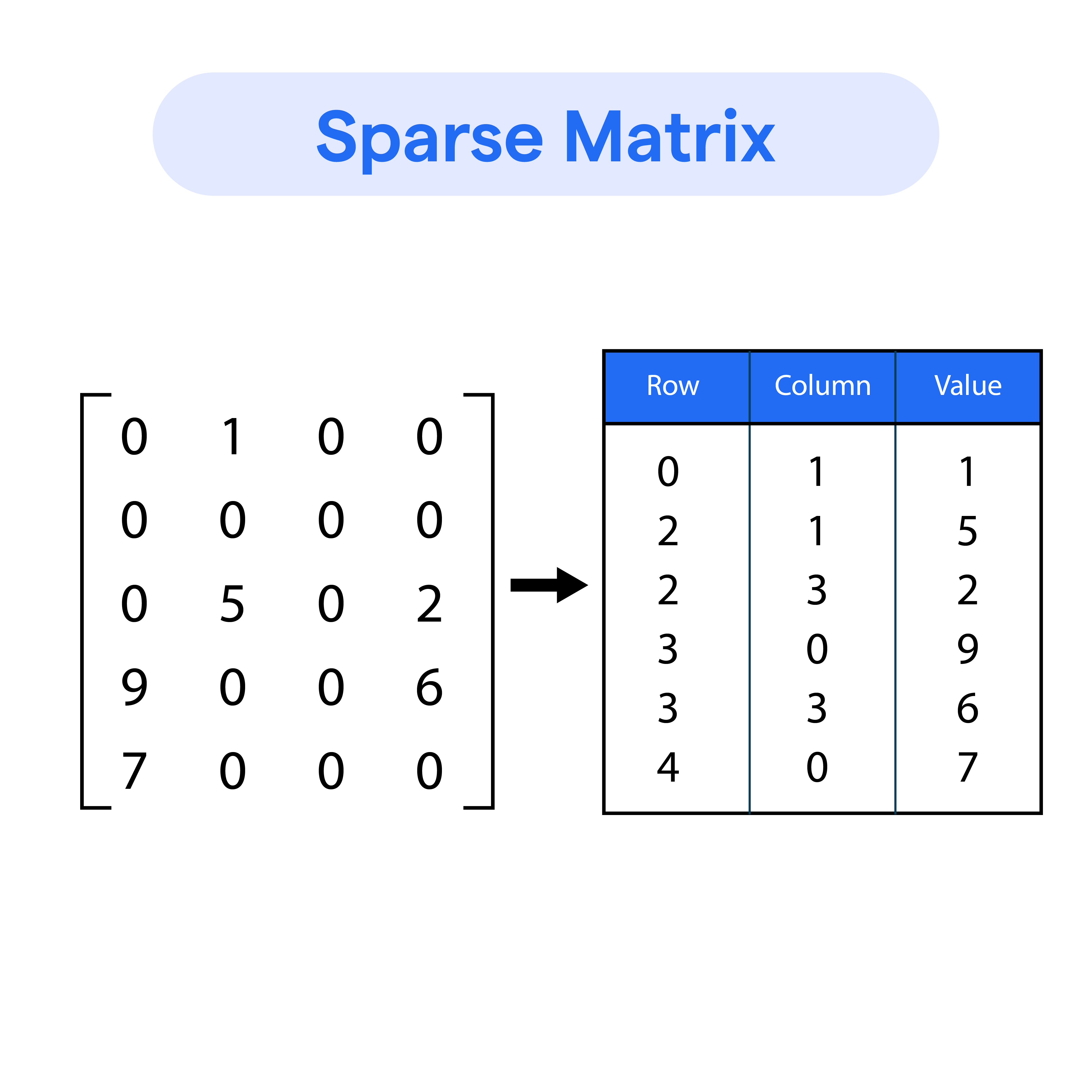
What is a Sparse Matrix?
A sparse matrix is a special type of matrix in mathematics wherein the majority of its elements are zero. In contrast to dense matrices, which contain a significant number of non-zero elements, sparse matrices have very few non-zero values. This unique attribute makes sparse matrices ideal for certain applications where computational and memory efficiency is paramount.
Theoretical Representation of Sparse Matrices
A sparse matrix can be represented as a data structure, which has rows, columns, and non-zero elements. The theoretical representation of a sparse matrix can be written as S = {(i, j, v): i ∈ R, j ∈ C, v ∈ V}, where R represents the set of row indices, C corresponds to the set of column indices, and V signifies the set of non-zero values.
Why Sparse Matrices?
Sparse matrices are essential due to their unique characteristics, which make them highly suitable for distinct use cases.
Storage Efficiency
One of the main advantages of sparse matrices is their ability to save storage. Since the majority of the elements are assumed zero, only the non-zero elements and their corresponding positions need to be stored. This can lead to substantial storage and memory savings, particularly in large-scale problems.
Computational Efficiency
When it comes to executing operations on sparse matrices, only the non-zero elements are considered, significantly reducing the computational time compared to dense matrices. This makes sparse matrices an invaluable tool in computational efficiency for various applications.
Real-world Applications
Sparse matrices are not just theoretical constructs but have practical applications in diverse fields. From large-scale simulations in engineering, bioinformatics, and physics to graph representations and machine learning algorithms, sparse matrices are extensively utilized in real-world scenarios.
When Sparse Matrices Arise?
Sparse matrices are prevalent in real-life situations, and understanding when they emerge can help identify their suitability for specific applications.
Engineering and Physics Simulations
Sparse matrices are widely applied in engineering and physics simulations that involve large numbers of variables, especially those governed by partial differential equations (PDEs). Many PDEs end up generating sparse systems of linear equations when discretized.
Graph Representations
Graphs are mathematical structures commonly used for modeling relationships among objects. In applications such as social networks, web analytics, or transportation networks, the adjacency matrices built for representing the graphs have a large number of nodes and can be incredibly sparse.
Text Mining and Natural Language Processing
Sparse matrices often arise in text mining and natural language processing (NLP) applications, such as the bag-of-words model (BoW) or term-document matrices, where word occurrences in each document are stored. Typically, only a small percentage of the possible words occur in a specific document, generating sparse matrices.
Recommender Systems
In the realm of recommender systems, especially collaborative filtering algorithms, the user-item interaction matrix can be sparsely populated, since users would likely rate or interact with only a fraction of available items.
Machine Learning Algorithms
Various machine learning models and algorithms benefit from sparse matrices when dealing with sparse data inputs, such as in feature extraction or dimensionality reduction techniques.
How to Represent Sparse Matrices?
While they save memory and improve computational efficiency, sparse matrices need to be represented optimally to meet these objectives.
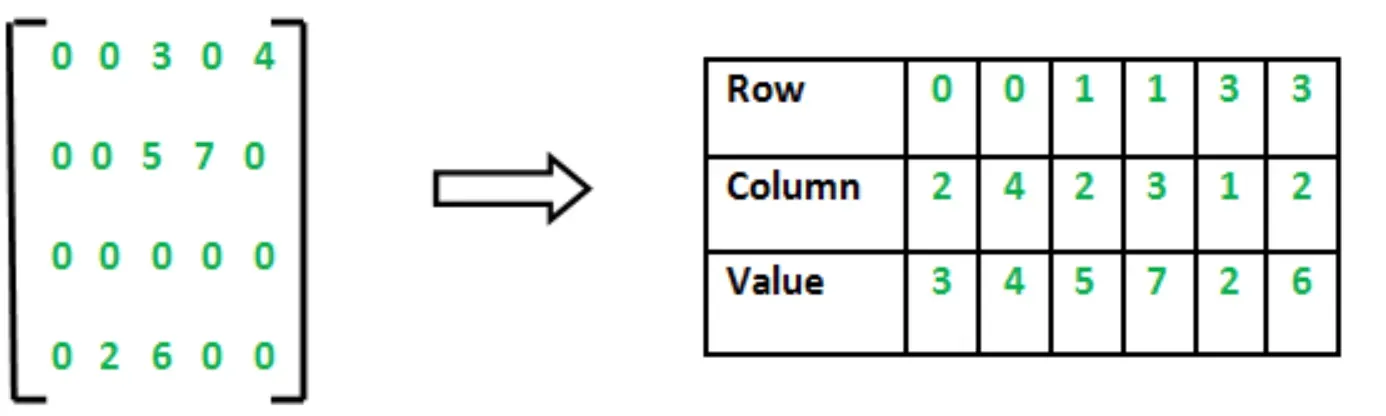
Coordinate List (COO)
In the COO format, a sparse matrix is represented by three parallel arrays for the row indices, column indices, and values of non-zero elements.- This format is memory efficient and allows for easy construction and manipulation but may not be as computationally efficient for certain arithmetic operations.
Compressed Sparse Row (CSR)
The CSR format efficiently stores a sparse matrix using three arrays: row pointers, column indices, and non-zero values. The row pointers contain the indices of the first non-zero element in each row, the column indices store the column position of each non-zero element, and the non-zero values are self-explanatory. This method allows for efficient arithmetic operations and is suitable for row-based applications.
Compressed Sparse Column (CSC)
CSC format is analogous to CSR but with a column-based representation. In this case, an array of column pointers, row indices, and non-zero values is used. The CSC format is effective in column-based operations and algorithms.
Dictionary of Keys (DOK)
The DOK format represents sparse matrices using a dictionary or associative array that stores the non-zero elements as key-value pairs, where the keys are the corresponding row and column indices. This method facilitates straightforward element insertion and removal, although it might not be computationally efficient for arithmetic operations.
Other Formats
There are numerous other specialized sparse matrix representations, such as diagonal storage format (DSF), Ellpack-Itpack format (ELL), and Block Compressed Row (BCR), which cater to specific types of sparse matrices or computational requirements.
Operations on Sparse Matrices
Understanding how to perform arithmetic operations on sparse matrices is crucial for their effective utilization in a variety of applications.
Matrix Addition
The addition of two sparse matrices can be performed efficiently using the COO or DOK formats. The operation involves iterating through the non-zero elements of each matrix and updating the sum accordingly.
Matrix Multiplication
Matrix multiplication can be efficiently carried out in either the CSR or CSC format. Row-based matrix-vector multiplication benefits from the CSR format, while column-based operations prefer the CSC format.
Element-wise Operations
Element-wise operations, such as addition and multiplication, can be implemented effectively in the DOK or COO formats. By iterating through non-zero elements, these operations can be performed with minimal computational effort.
Transpose and Inversion
Transposing a sparse matrix is often straightforward, especially in the COO, CSR, or CSC formats. Inverting a sparse matrix, however, is a computationally intensive task and requires specialized algorithms, such as Gaussian elimination for sparse matrices.
Solving Linear Systems
Solving sparse linear systems of equations is a common task in practice. Several algorithms have been devised to execute this efficiently, such as the conjugate gradient method, GMRES, or sparse LU decomposition.
Software Libraries for Sparse Matrices
To leverage the benefits of sparse matrices effectively, numerous software libraries have been developed.
SciPy
The SciPy library in Python encompasses several sparse matrix representations and algorithms, such as CSR, CSC, and DOK formats, as well as routines for linear algebra and matrix operations.
Eigen
Eigen is a C++ template library that supports sparse matrix representations and operations, including basic arithmetic and linear system solvers, with an easy-to-use syntax.
Trilinos
Trilinos is a collection of C++ libraries that focuses on large-scale, high-performance scientific computing, including support for parallel sparse matrix operations and distributed memory computing.
SuiteSparse
SuiteSparse is another C library that incorporates a variety of algorithms and data structures for sparse matrix operations, including matrix factorization, linear solvers, and graph algorithms.
MATLAB
MATLAB has built-in support for sparse matrices, including the creation, manipulation, and visualization of these matrices, as well as its own suite of sparse-specific operations and functions.
Practical Limitations and Challenges
Despite their utility, sparse matrices come with their own set of constraints and challenges that need to be considered for successful implementation in practice.
Format Selection
Choosing an appropriate format for representing sparse matrices is crucial for specific applications. The format should balance memory efficiency, computational efficiency, and ease of implementation, depending on the task at hand.
Computational Complexity
Sparse matrix operations may still be computationally expensive for large-scale problems, even when utilizing specialized algorithms. Careful consideration of how memory is allocated and accessed during arithmetic operations is required to ensure efficiency.
Balancing Sparsity
There is often a trade-off between maintaining a sparse matrix and performing operations that may alter the matrix's sparsity. Care should be taken to adjust operations in order to preserve sparsity or explore different representations and algorithms to maintain efficiency.
Best Practices with Sparse Matrices
Working with sparse matrices, like with any complex data structure, necessitates operating by certain recommended practices for optimal results.
Appropriate Format Selection
The choice of sparse matrix representation has a significant impact on the efficiency of computations. The format should be chosen based on the characteristics of the data and the operations to be performed.
Optimizing for Computation
Careful consideration should be given to the computational operations that need to be executed. Certain matrix formats excel in certain types of operations, so optimization efforts should reflect these nuances.
Balancing Sparsity during Operations
In performing operations on sparse matrices, it's crucial to maintain the sparsity of the matrix. If an operation modifies the matrix's sparsity, it can lead to increased storage and computational costs.
Use of Specialized Libraries
Numerous libraries have been developed to simplify interactions with sparse matrices. Leveraging these packages can help streamline tasks and achieve better computational performance.
Parallel and Distributed Computing
Given the large size of some sparse matrices, parallel and distributed computing can be highly effective. Implementations should aim to take full advantage of concurrent processing capabilities where possible.
Practical Examples of Sparse Matrices
To illustrate the role of sparse matrices in real-world scenarios, let's delve into a few practical examples.
PageRank Algorithm
Google's PageRank algorithm, which ranks webpages based on their importance, leverages the power of sparse matrices. The internet can be modeled as a massive graph with nodes and links between them represented as a sparse matrix. Through the application of eigen-decomposition on this sparse matrix, the PageRank scores can be achieved.
Social Network Analysis
In social network analysis, sparse matrices can mirror the relationships among users. For a large network with millions of users, the user-to-user relationships denoted as the adjacency matrix can be extremely sparse, making sparse matrices an efficient representation.
Density-Based Spatial Clustering of Applications with Noise (DBSCAN)
The DBSCAN clustering algorithm, widely used in machine learning, uses a sparse matrix of neighborhood relationships. This use of a sparse matrix streamlines computation, as instead of working with dense distance matrices, the algorithm only needs to consider the sparse connections between data points within a certain radius.
Inverse Document Frequency (TF-IDF)
In natural language processing, one common approach to document vectorization and feature extraction is the TF-IDF algorithm. In this case, the document-term matrix, which stores the tf-idf scores for each term in every document, is a sparse matrix as every document contains only a small fraction of the possible terms.
The power of sparse matrices hinges on effective representation, optimal format selection, and adeptness at balancing sparsity during computations. While challenges do exist and require methodical attention, the significant benefits of sparse matrices make them an indispensable mathematical tool in an array of applications, including data science, machine learning, and engineering.
Frequently Asked Questions (FAQs)
In what scenarios is a Sparse Matrix preferable over a Dense Matrix?
A sparse matrix is preferable when the matrix has a large number of zero-value elements. It saves space and computational power in large datasets where non-zero elements are scarce.
How do Sparse Matrices save memory?
Sparse matrices save memory by only storing non-zero elements and their corresponding indices. This means less storage space is required compared to dense matrices, which store all values including zeros.
What types of operations can be optimized with Sparse Matrices?
Matrix operations like multiplication and addition can be optimized with sparse matrices, as computations can be limited to non-zero elements, reducing the computational load significantly.
Can Sparse Matrices be used in Machine Learning?
Yes, sparse matrices are widely used in machine learning to handle high-dimensional data, where data sets often contain many zeros and only a few relevant values.
What are common formats for Storing Sparse Matrices?
Common formats for storing sparse matrices include Coordinate (COO), Compressed Sparse Row (CSR), and Compressed Sparse Column (CSC). Each has its own advantages depending on the operations performed and the sparsity of the matrix.