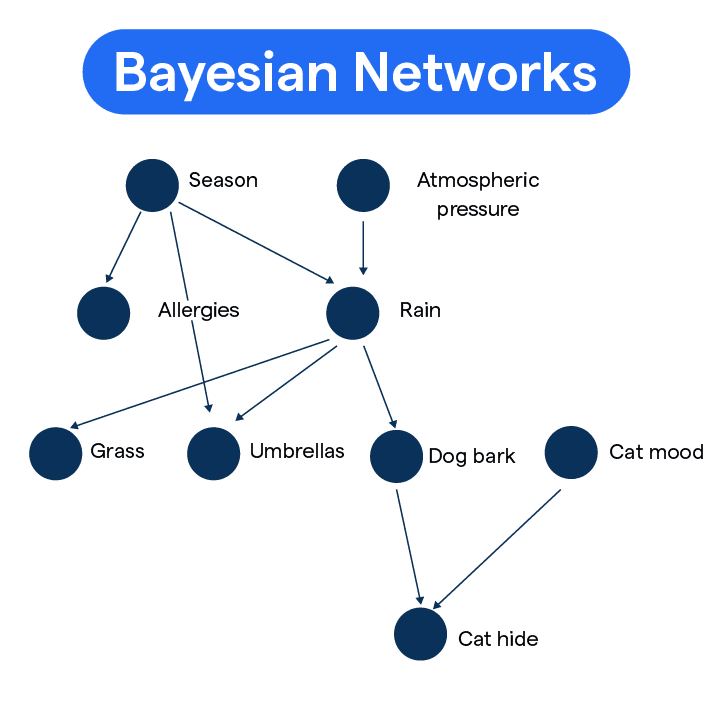
What is a Bayesian Network?
A Bayesian Network is a graphical model that encapsulates the probabilistic relationships among a set of variables. It allows us to predict outcomes, assess risks, and make decisions in uncertain situations.
The basic building blocks of Bayesian Networks are nodes and edges, with nodes representing variables. The edges, or lines connecting the nodes, represent causal relationships or dependencies. The connection signifies that the state of one variable can affect the state of another.
What makes Bayesian Networks "Bayesian?" Named after mathematician Thomas Bayes, these networks employ Bayes’ theorem, a principle in probability theory and statistics for updating probabilities of hypotheses when given evidence.
Why Use Bayesian Networks?
In many situations, Bayesian Networks can be a powerful tool for modeling complex systems and handling uncertainty.
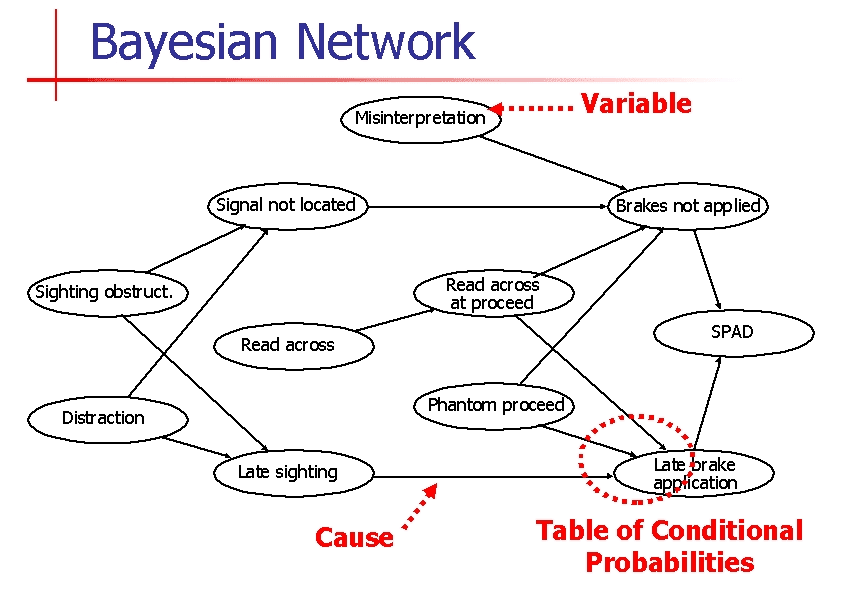
Modelling Complex Systems
Bayesian Networks can model data with multiple interacting variables and visualize the complex web of relationships between them. They provide a clear way to see the structure of the data and the conditional dependencies.
Handling Uncertainty
Bayesian networks thrive in uncertain situations. Operating based on probability, they grant us the capability to predict, plan and make informed decisions even when we don't have complete information.
Benefits of Bayesian Networks
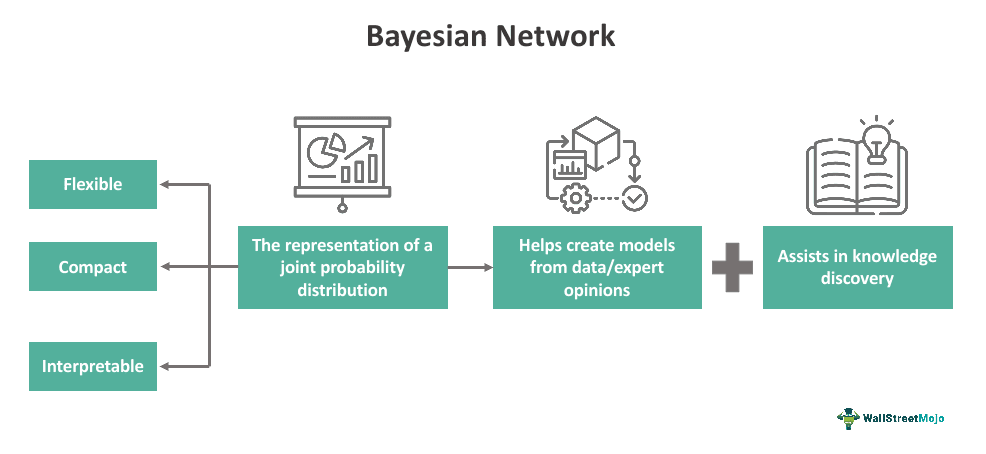
Like any relevant scientific model, Bayesian Networks come packed with a slate of benefits and advantages.
Clarity
Bayesian networks represent relationships and dependencies clearly in the form of a graph. This visual depiction helps us understand the effects of variables on one another.
Possibility of Intervention
With Bayesian networks, you can test different scenarios or interventions and observe the potential results. This allows the modeling of cause and effect, which is significant in decision-making processes.
Effective Data Usage
Bayesian networks can effectively use available data to update probabilities, making them useful in real-world applications where data is incomplete or uncertain.
Constraints of Bayesian Networks
Of course, Bayesian Networks aren't without their shortcomings. There are a few limitations to take into account.
Demanding Data Requirements
The construction of a Bayesian network requires sufficient data for the estimation of conditional probability tables. If data is scarce or incomplete, the network may not be accurate.
Complex Computation
While the visual representation is simple, the math behind Bayesian networks can be pretty intensive, especially when dealing with a complex problem with many variables.
Dependency Limitations
The network can only capture dependencies that have been specified by the analyst, meaning dependencies can be omitted if they are unknown or unanticipated.
Real-world Applications of Bayesian Networks
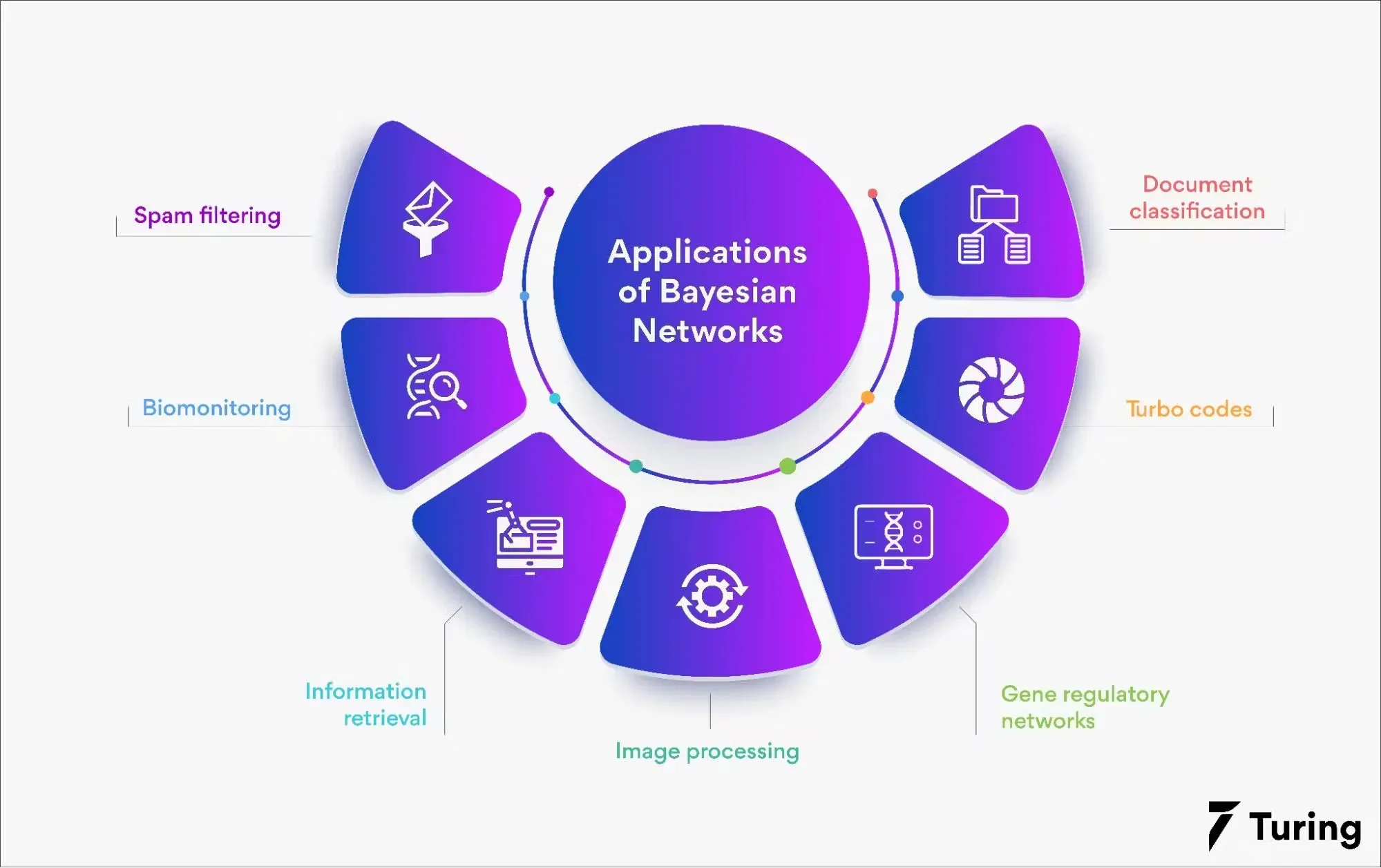
Bayesian Networks have a wide range of applications spanning various domains.
Medical Diagnosis
In medicine, Bayesian networks are used for diagnosis and prognosis, where variables can include symptoms, patient history, and genetic factors, among others.
Genetic Analysis
Geneticists use Bayesian networks to predict and analyze genetic diseases, taking a multitude of interrelated variables into account.
Decision-Making in Business
Businesses harness Bayesian networks for scenario analysis, resource allocation, and risk assessment to make informed decisions.
Bayesian Networks vs Other Models
Bayesian Networks are not the only game in town, and we ought to assess alternatives.
Decision Trees
Unlike decision trees that offer a path or sequence of decisions, Bayesian networks graphically represent the relationship between variables, providing a more comprehensive view.
Suggested Reading: Decision Trees: Benefits and Applications
Neural Networks
Neural networks are stronger for tasks like image recognition and natural language processing, while Bayesian networks excel at modeling uncertainty and cause-and-effect relationships.
Suggested Reading: Neural Network: Uses, Workings and Challenges
Regression Models
Regression models predict one variable based on others, while Bayesian networks model and visualize the interconnected web of all related variables.
Frequently Asked Questions (FAQs)
What exactly is a Bayesian Network?
A Bayesian Network is a statistical model that uses graph theory to depict relationships among variables based on probability theory, particularly Bayes' theorem.
How do Bayesian Networks work?
Bayesian Networks use nodes to represent variables and edges to represent their relationships. They utilize conditional probability to interpret uncertain situations.
Why are Bayesian Networks useful?
They can model complex systems and deliver a clear picture of a problem, leveraging available data to update probabilities and predict outcomes even under uncertainty.
What are some applications of Bayesian Networks?
Bayesian Networks find applications in many fields, including medical diagnosis, genetic analysis, and business decision making.
How do Bayesian Networks compare to other models?
Compared to decision trees, neural networks, and regression models, Bayesian networks offer a more comprehensive overview of interrelated variables and superior performance in handling uncertainty.
