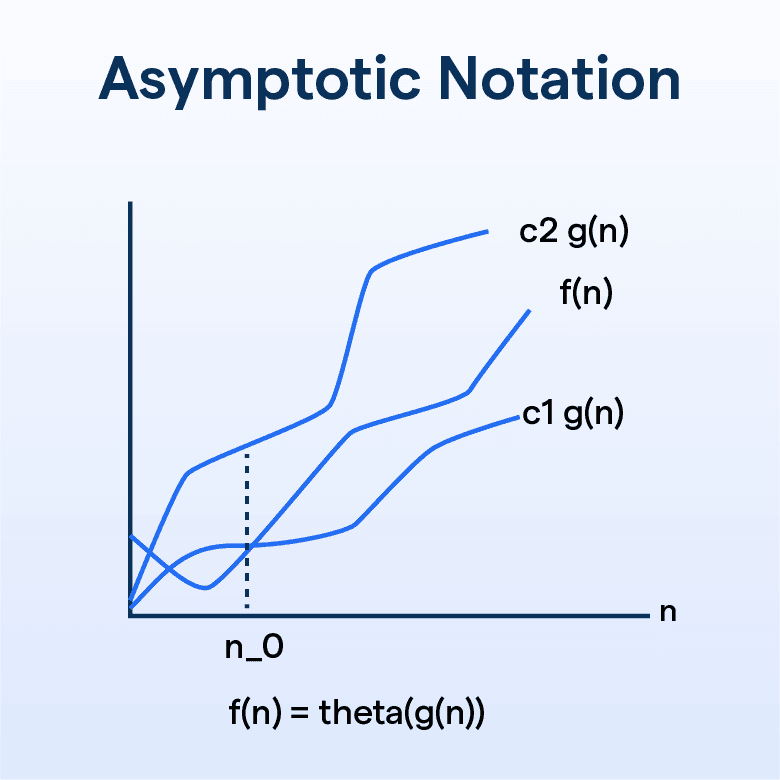
What is Asymptotic Notation?
Asymptotic notation is a set of mathematical notation used to describe the performance or complexity of algorithms in computer science. It gives an upper, lower, or average limit for performance, helping you judge an algorithm's efficiency.
When evaluating algorithms, especially their time and space complexity, asymptotic notation is indispensable. It visualizes an algorithm's efficiency under different conditions, helping developers optimize their code.
Asymptotic notation lets developers determine how their algorithms will scale, helping them make critical decisions when dealing with big data or resource-limited systems.
Fundamentals of Asymptotic Notation
In asymptotic notation, we typically ignore constant factors. This is because, as the input size grows large, the constants become less significant compared to the growth rate.
Coefficients
Just like constants, coefficients are often disregarded in asymptotic notation, focusing on the growth rate rather than specific numerical values.
Big O Notation
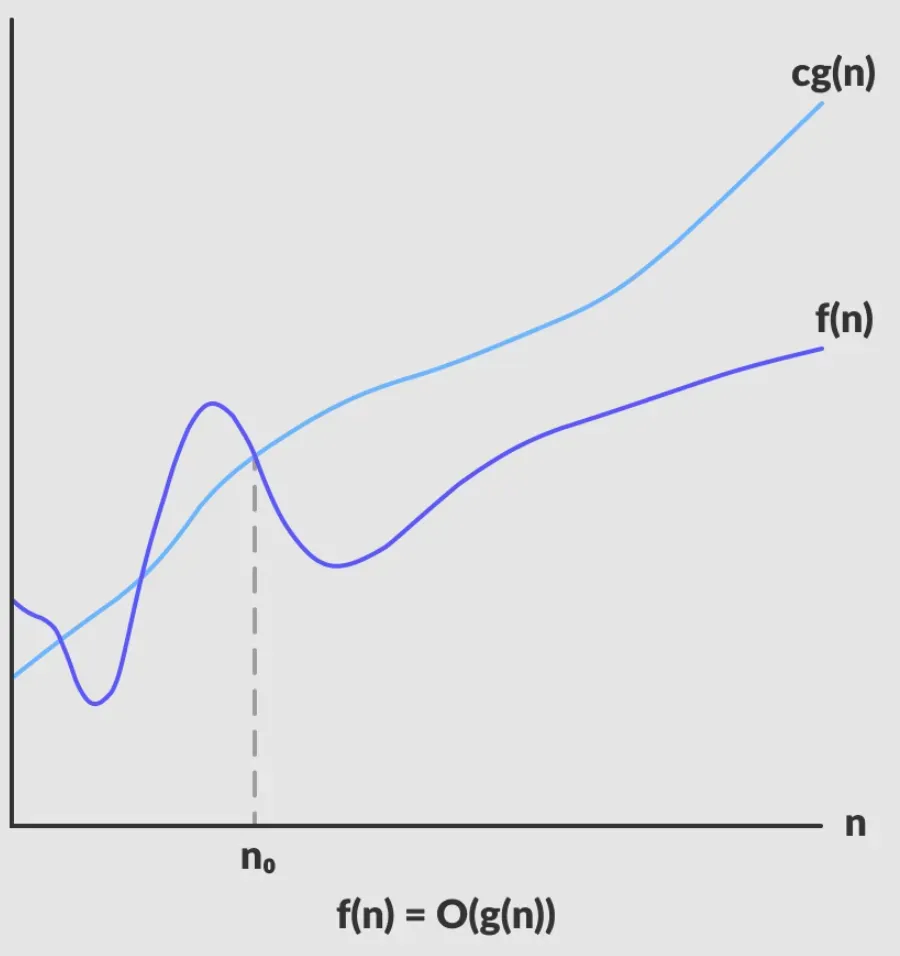
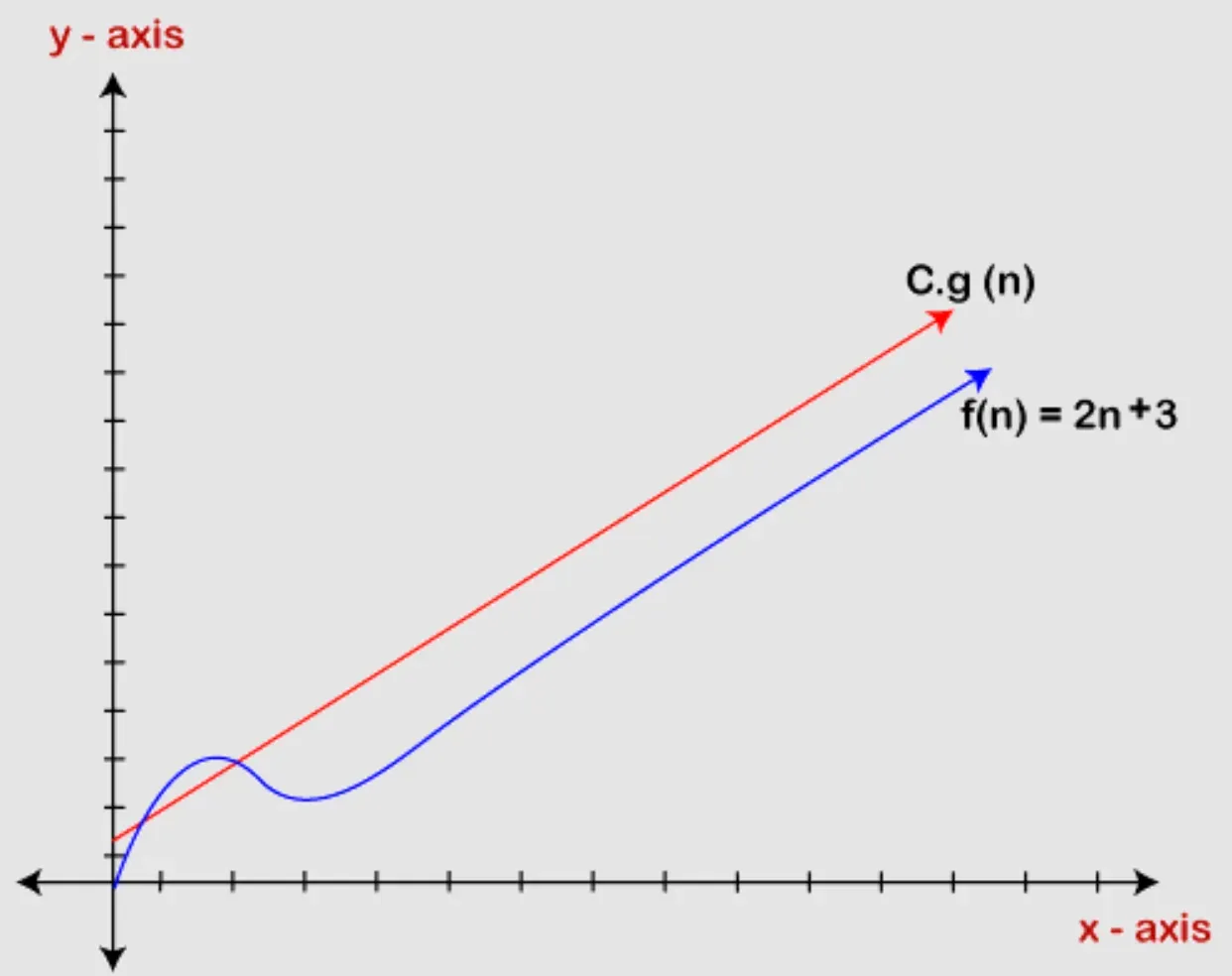
Big O notation describes an upper bound on the time complexity of an algorithm. It gives the worst-case complexity, helping you understand the maximum resources your algorithm may demand.
Big Omega Notation
On the other hand, Big Omega notation provides a lower bound on the time complexity. It describes the best-case scenario, revealing how efficient your algorithm could be.
The Components of Asymptotic Notation
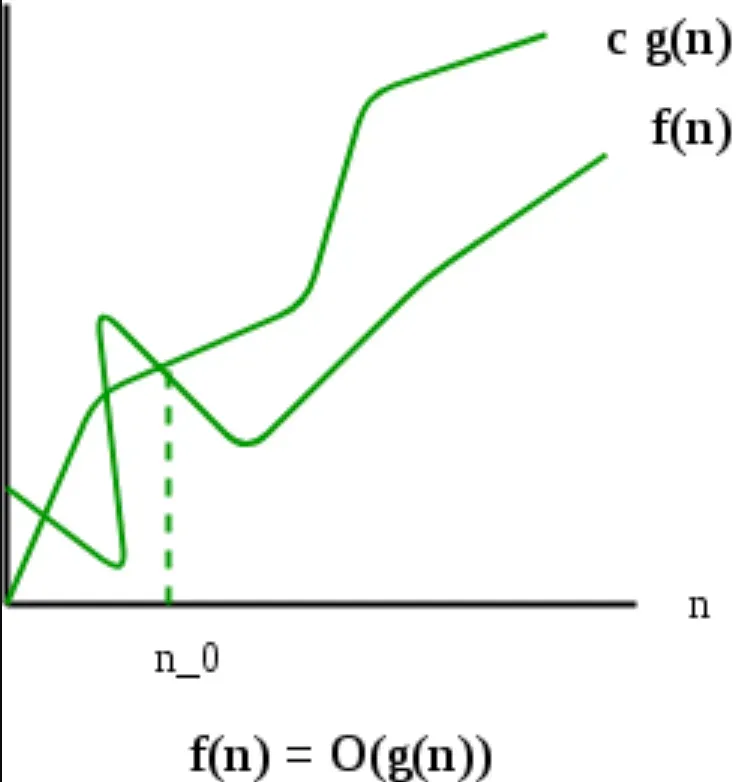
Growth rates play an essential role in determining the big O, Omega, or Theta of an algorithm. They describe how the algorithm's performance scales with the input size.
Bounding Functions
The functions used in the asymptotic notation, like O(n), O(n^2), etc., bound the algorithm's performance. They abstract the critical behavior of the function representing the algorithm's performance.
Variables
In asymptotic notation, variables represent the size of an input to the algorithm. As the variable increases, it showcases how the algorithm scales.
Co-dominant Terms
In expressions with multiple terms, we often focus on the dominant term - the term that grows the fastest. Co-dominant terms are those that share the same exponent and therefore grow at the same rate.
Interpreting Asymptotic Notation
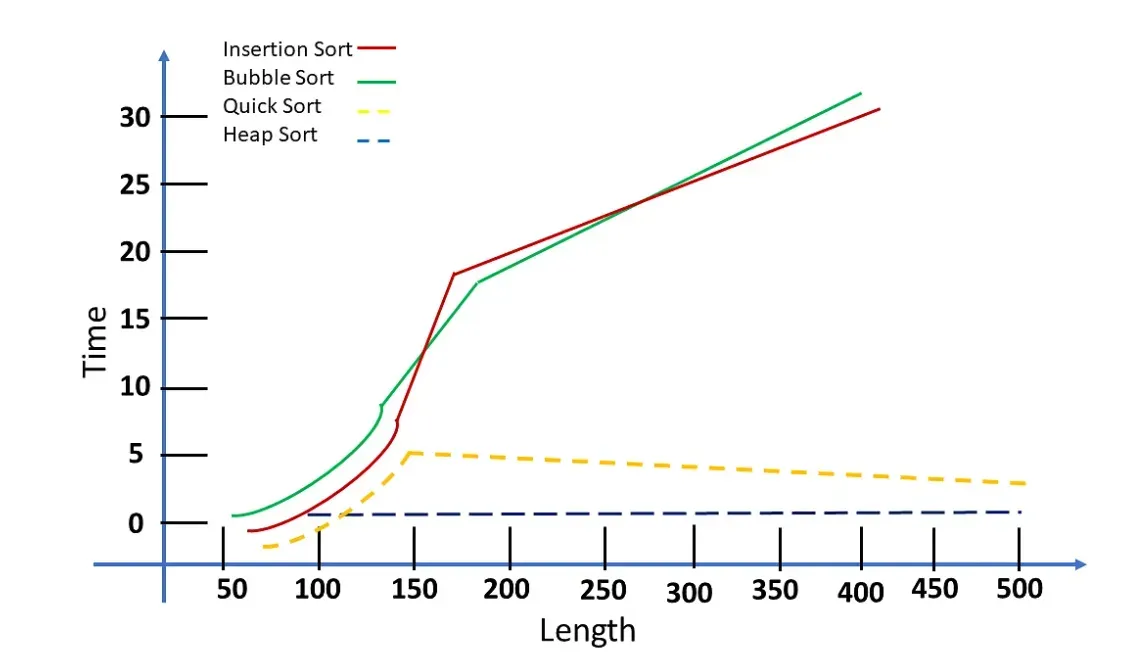
The Big O complexity chart offers a visual method to compare the time or space complexity of algorithms as described by Big O notation.
Time vs Space Trade-off
Asymptotic notation can help programmers see the time-space trade-offs. An algorithm might have excellent time complexity (fast), but horrible space complexity (uses a lot of memory), and vice versa.
Worst vs Best Case
Asymptotic notation offers an insight into the worst-case and best-case scenarios. These provide boundaries within which the performance of an algorithm would lie.
Average Case Complexity
This represents the expected behaviour of an algorithm under random inputs. It's an essential part of understanding the practical efficiency of an algorithm.
Applications of Asymptotic Notation
Understanding the asymptotic notation of an algorithm can help identify potential bottlenecks and areas of improvement.
Choice of Algorithms
Often, when multiple algorithms can solve a problem, asymptotic notations can guide programmers in choosing the most efficient one.
Predicting System Performance
In real-world problems, asymptotic notations provide a way to predict how a system or algorithm will perform on larger datasets.
Building Scalable Systems
For systems designed to handle large amounts of data, asymptotic notation is essential in guiding the design and architecture to ensure scalability.
Suggested Reading:
Loss Function
Common Asymptotic Notation Terms
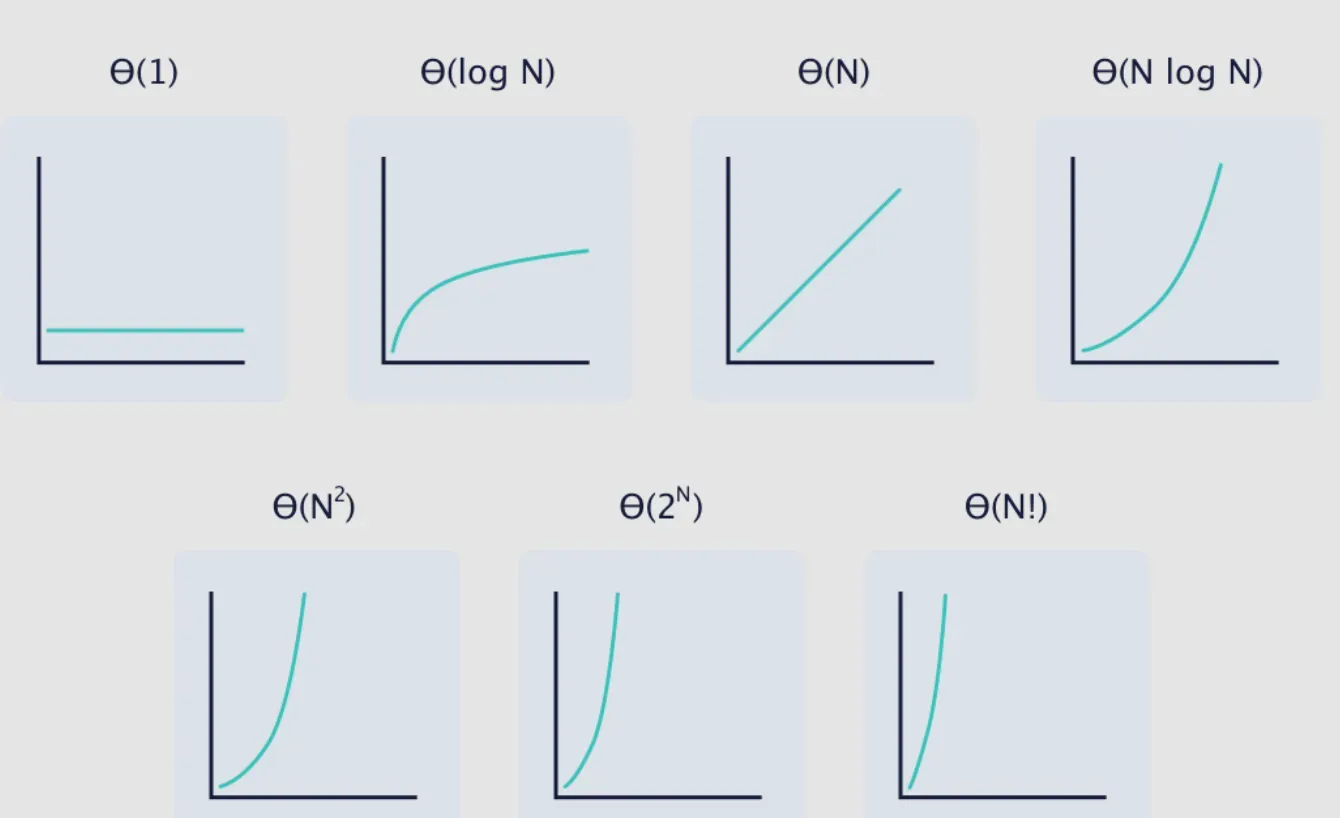
Constant Time - O(1)
Constant time complexity means the execution time doesn't change with the size of the input. It's the most desirable time complexity.
Linear Time - O(n)
Linear time complexity implies that the running time of an algorithm is directly proportional to the size of the input.
Quadratic Time - O(n²)
Quadratic time complexity signifies that the running time of an algorithm is proportional to the square of the size of the input.
Logarithmic Time - O(log n)
Logarithmic time complexity is highly desirable, especially for large data sets. It means that the algorithm significantly reduces the input size at each step.
Frequently Asked Questions (FAQs)
What is Asymptotic Notation?
Asymptotic notation is a mathematical notation used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity.
It's widely used in computer science for analyzing and comparing algorithms.
What does Big O notation mean?
Big O notation is the most commonly used asymptotic notation. It describes an upper bound on the time complexity of an algorithm, thus providing its worst-case complexity.
What is Big Omega notation?
Big Omega notation describes a lower bound on the time complexity. It paints a picture of the best-case scenario of an algorithm's performance.What does O(n), O(1), O(n²) mean?
These are specific terms within Big O notation. O(n) means the algorithm's time complexity scales linearly with input size. O(1) is constant time complexity, meaning time taken doesn't change with input size. O(n²) means the time complexity is proportional to the square of the input size.
Why is Asymptotic Notation important in computer science?
Asymptotic notation helps compare algorithms based on their efficiency. It provides a way to understand how things scale when dealing with big data or complex computations—ultimately, aiding the design of better, more efficient algorithms and systems.