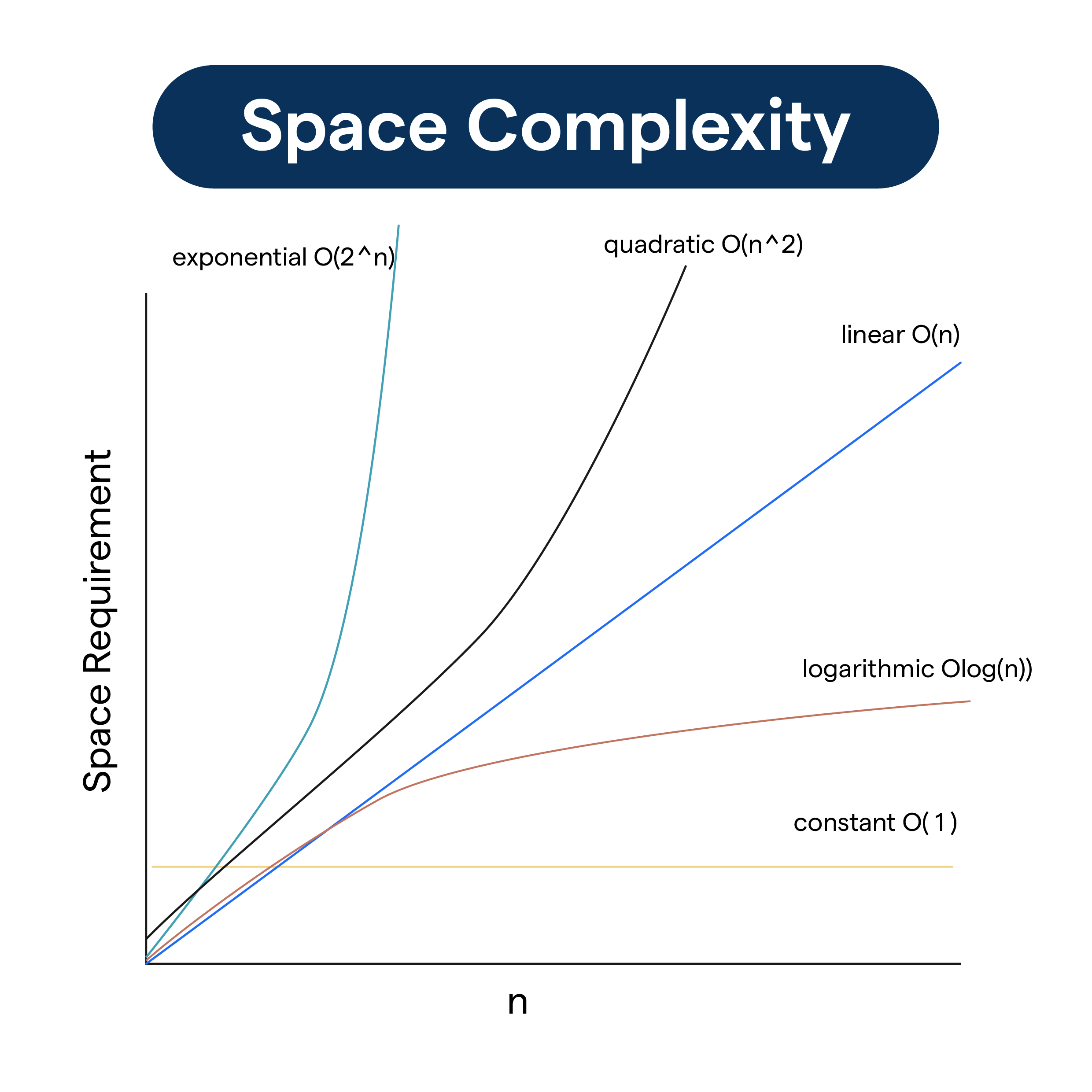
What is Space Complexity?
Space Complexity is a term used in computer science to describe the amount of memory, or space, an algorithm or a computational process requires to solve a problem.
Defining Space Complexity
Space complexity analyzes the maximum amount of memory taken by an algorithm to complete its execution. It can be quantitatively measured in terms of the number of memory units used.
Importance
The understanding of space complexity is important in assessing the efficiency of an algorithm. It helps in determining whether an algorithm is feasible and suitable for a particular system depending upon the memory constraints.
Factors Influencing Space Complexity
Space complexity is influenced by two components: fixed space requirements (independent of the size of the problem) and variable space requirements (changing with the size of the problem).
Understanding Space Complexity in Relation to Time Complexity
Space complexity, along with time complexity, is fundamental to Big O Notation, which provides a measure of the complexity of an algorithm.
While time complexity addresses the speed of an algorithm, space complexity focuses more on the resources it requires.
Who Uses Space Complexity?
Space Complexity is a critical factor taken into account by various professionals in the field of computer science and programming.
Role in Software Development
Software developers often use space complexity assessments to optimize their applications, ensuring they are not overly memory-intensive.
Significance for Data Scientists
Data Scientists use the concept of space complexity while developing algorithms for data processing and modeling.
Application in Algorithm Design
Computer Scientists involve space complexity when designing and implementing algorithms.
Importance in Database Management
Database Administrators consider space complexity while performing operations like sorting and searching to maintain system performance.
Use in Computer Networking
In computer networking, space complexity comes into play when dealing with data storage and transmission, influencing decisions on buffer size, cache management, and more.
When is Space Complexity Applied?
The concepts of space complexity apply across various stages of the computational process.
Algorithm Design Phase
Space complexity is often considered at the algorithm design phase, where developers select or design algorithms based on their space requirements.
Debugging Process
During debugging, if a program is found to be excessively consuming memory, space complexity can help identify inefficient algorithms or data structures.
System Optimization
When optimizing a system's performance, understanding space complexity can guide memory management techniques.
Resource Allocation
In decisions concerning resource allocation, space complexity helps developers make memory-efficient choices.
Trade-Offs between Time and Space Complexity
When dealing with trade-offs between time and space complexity, understanding both concepts helps developers make more informed decisions.
Where is Space Complexity Used?
Space complexity is applied across various fields where programming and algorithmic computations are involved.
Programming
In programming, particularly in system-level programming, where memory usage is important, space complexity often guides the choice of data structures and algorithms.
Data Mining
In the field of data mining, algorithms dealing with large datasets need to consider space complexity to manage memory efficiently.
Software Development
In software development, particularly in embedded systems where memory is limited, understanding space complexity is crucial.
Database Systems
In designing and maintaining database systems, space complexity comes into play in the optimization of database operations.
Operating Systems
In designing operating systems, space complexity is used in algorithm selection, particularly for resource management and process scheduling.
Why Do We Need Space Complexity?
Understanding space complexity is critical in the computer science and programming fields for several reasons.
Efficiency of Programs
A firm grasp of space complexity allows developers to optimize their programs' efficiency, reducing excess memory usage.
Better Algorithm Selection
Knowledge about space complexity aids in better algorithm selection, which ultimately impacts the memory usage of the program.
Informed Tradeoffs
Understanding space complexity can help make informed tradeoffs between space and time, focusing on maximum efficiency and minimum resource utilization.
Resource Optimization
Awareness of an algorithm's space complexity aids in better resource management and process scheduling in diverse computing environments.
Development of Scalable Solutions
Space complexity is a significant attribute for developing scalable solutions. As the problem size grows, algorithms with lower space complexity will be more scalable.
How to Calculate Space Complexity?
Space complexity computation can seem complex. However, once you break it down, it can be quite straightforward.
Auxiliary Space
Calculation of space complexity begins with considering the auxiliary space, which includes the extra space or the temporary space used by the algorithm.
Space Used by Variables and Constants
Factor in the space used by variables and constants. Even though these may seem trivial compared to larger datasets, they are still a part of the computations.
Input and Output Space
Consider the space required to store the input and output. In cases where an algorithm requires a large data structure like a matrix, this can significantly contribute to the space complexity.
Recursive Function Calls
If an algorithm utilizes recursive function calls, remember to consider the stack space, which may increase the space complexity.
Total Space Complexity
Once all factors are considered, the sum of all these gives us the total space complexity.
Best Practices for Optimizing Space Complexity
Optimizing space is a challenging aspect of programming and algorithm designing, but with certain practices, it can be managed effectively.
Opt for Space-efficient Data Structures
Using space-efficient data structures, where possible, can significantly reduce an algorithm's space complexity.
Limit Use of Recursive Function Calls
Recursive function calls can lead to excess space usage due to stack space requirements, so they should be used judiciously.
Reuse Variables
Reusing variables wherever it's possible can help in saving the memory used by the program.
Incremental Data Loading
When dealing with large datasets, loading data incrementally, instead of all at once, can help optimize space usage.
Efficient Garbage Collection Implementation
Implementing efficient garbage collection can help free up memory that isn't being used by the program anymore.
Best Practices for Optimizing Space Complexity
Striking a balance between resource usage and efficiency is important. Here's how to optimize space complexity.
Use of Space-Efficient Data Structures
Data structures form the core of an algorithm, and their choice significantly impacts the space complexity.
For example, choosing a hash map over a list can lead to considerable space optimization when solving problems related to frequency counts.
Similarly, when dealing with hierarchical data, trees are more space-efficient compared to storing data in multiple lists or arrays.
Limiting Use of Recursive Function Calls
Recursive function calls are a common cause of high space complexity due to the requirement of additional stack space.
For instance, the recursive implementation of Fibonacci sequence generation has higher space complexity than its iterative counterpart due to the additional space required to store the recursive stack.
Reusing Variables
Conserving memory can be as simple as reusing variables. The practice of declaring new variables constantly, especially within loops or repetitive processes, can add onto space complexity. Being conscientious about reusing variables can help.
Incremental Data Loading
When dealing with large datasets, loading them incrementally from disk or network, rather than all at once into memory, can optimize space usage.
Efficient Garbage Collection Implementation
In languages with garbage collectors, ensuring efficient garbage collection can help free up memory that isn't being used by the program anymore.
Challenges in Managing Space Complexity
Overcoming the complexities of optimizing algorithms for space can be difficult. Here are a few key challenges.
Time-Space Trade-Off
Balancing the trade-off between time complexity and space complexity may be challenging. Certain algorithms may solve problems faster but require more space, while others may be slower but consume less memory.
The compromise often depends on the particular application and its memory or speed requirements.
Language Limitations
Certain programming languages inherently have limitations when it comes to space optimization.
Static languages tend to give more control over memory management, while dynamic languages take this control away, often resulting in higher space usage.
Computational Complexity
Determining space complexity itself can be a challenge, especially when using advanced data structures and recursive functions.
The computational complexity involved can lead to difficulties in accurately determining the space requirements.
Scalability
As the size or volume of the problem grows, managing space complexity becomes difficult.
Large datasets can quickly overwhelm an algorithm's space requirements, leading to scalability concerns.
Hardware Restrictions
Each system or device has a limitation on the amount of available memory.
Thus, high space complexity can pose significant challenges, especially in embedded systems or older hardware with lower memory specifications.
Examples of Space Complexity
Let's look at a few examples to understand space complexity better.
Addition of Two Numbers
Consider a simple program to add two numbers. The space complexity of this program will include memory for variables that store the numbers, the memory to store the result, and any additional overheads.
The space complexity does not change with the size of the number being added. Hence, it's said to have constant space complexity, denoted as O(1).
Finding the Factorial of a Number
Consider a recursive function that finds the factorial of a number. The function has to remember the intermediate variables at each recursion level, thereby increasing the space complexity.
Thus, the space complexity is directly related to the size of the input (n), i.e., the number for which we are computing the factorial. In such cases, the space complexity is said to be linear, represented as O(n).
Matrix Operations
Consider the task of performing an operation on a matrix (like rotation or transformation). It often involves storing the entire matrix in memory, and the space complexity increases proportional to the size of the matrix.
Assuming the matrix is of size n x n, the space complexity will be quadratic, noted as O(n^2). If a temporary matrix is used during the computation, it further adds to the space complexity.
Recent Trends in Space Complexity Management
As with many aspects of computer science, managing space complexity is also evolving with new trends and advancements.
Emergence of Space-efficient Data Structures
In recent years, there has been an emergence of new space-efficient data structures that aim to optimize memory usage.
Cloud-Based Solutions
Cloud-based solutions provide a way to manage space complexity by providing virtually unlimited memory resources based on demand.
Advanced Garbage Collection Algorithms
There is continuous development in the field of garbage collection algorithms to manage unused memory more efficiently.
Software Specific Hardware
With the evolution of software-specific hardware like TPUs and ASICs, it becomes easier to deal with large amounts of data, managing space complexity efficiently.
Machine Learning based Optimization
Machine learning techniques are being incorporated to predict and optimize the space complexity of programs dynamically.
Space complexity holds a crucial role in the efficient designing and execution of algorithms. Mastering this concept enables programmers to effectively allocate memory resources, choose the right algorithms based on a system's limitations, and build scalable solutions.
The continuous advancements in the field of computer science are also ensuring better methods for managing space complexity.
This knowledge is not just essential for current scenarios but will continue to be critical in the future, with the ever-increasing data sizes and computing complexities.
Frequently Asked Questions (FAQs)
What exactly is Space Complexity in Computing?
Space complexity measures how memory usage grows with the input size in a program. It's a critical factor for optimizing programs, primarily in space-constrained environments.
How is Space Complexity different from Time Complexity?
While time complexity quantifies the time-efficiency of an algorithm, space complexity focuses on its memory-efficiency, portraying a trade-off between the two.
How Important is Space Complexity in Big Data?
With massive data sets, space complexity is vital. Optimizing space complexity can improve performance significantly when handling big data.
What is Auxiliary Space in the context of Space Complexity?
Auxiliary space is the extra temporary space (aside from input and output) that an algorithm uses during execution. It's a critical component of space complexity.
Can Recursive Algorithms affect Space Complexity?
Yes, recursive algorithms create a new stack frame for each recursive call, potentially increasing space complexity and in some cases leading to stack overflow.
