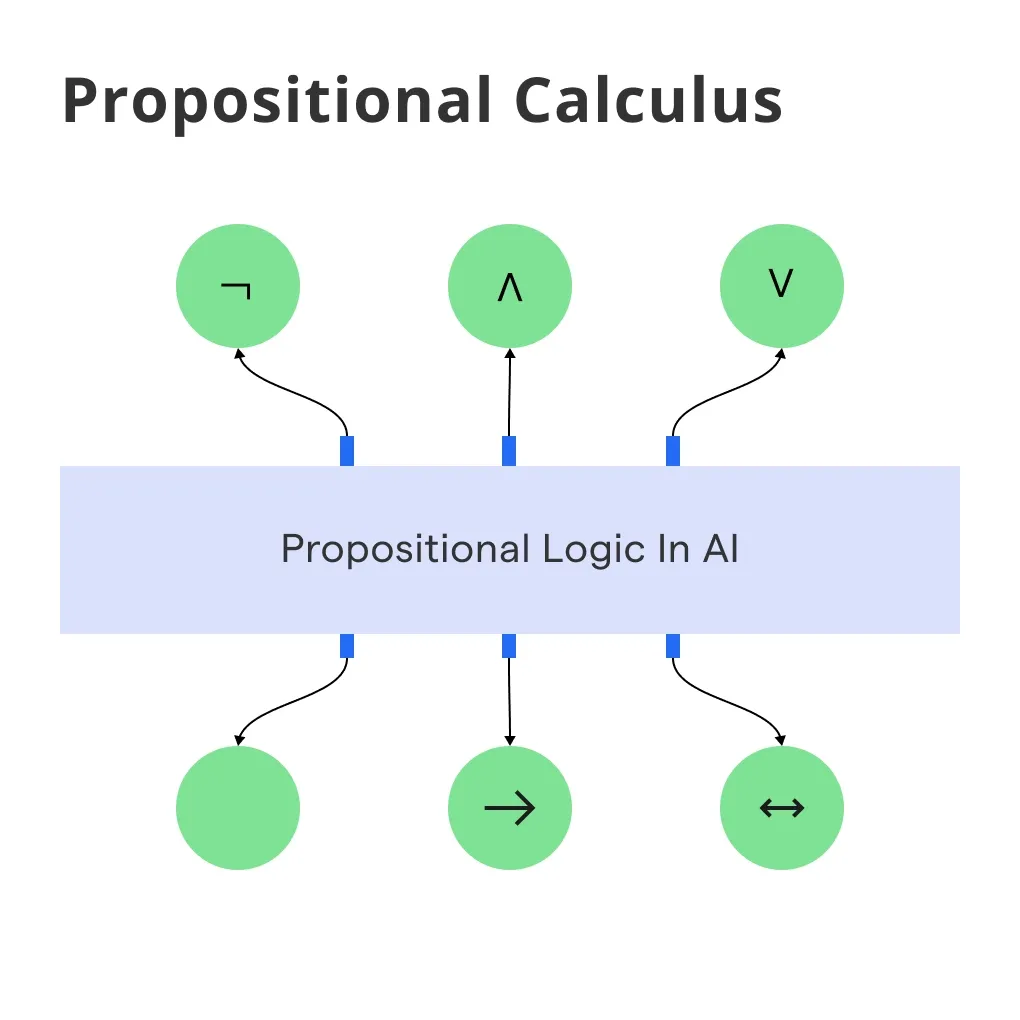
What is Propositional Calculus?
Propositional calculus, also known as propositional logic, is a branch of logic. It addresses and explores propositions, which are statements that can either be true or false.
The Basic Idea
At the heart of propositional logic lies the concept of a proposition. A proposition is a declarative statement that can be either true or false but not both.
Components of Propositional Calculus
Propositional calculus involves logical operations and connectives that occur between different propositions to form compound propositions.
Notation
There's a specific notation used in propositional calculus, such as P, Q, and R to denote propositions and ∨, ∧, ¬, →, and ↔ to denote connectives.
Use in Computer Science
Propositional calculus is widely used in computer science. It serves as the backbone of programming structures such as conditional statements and loops.
Who Uses Propositional Calculus?
While it might seem like a highly specialized topic, the truth is, that many individuals across different professions use propositional calculus in their work.
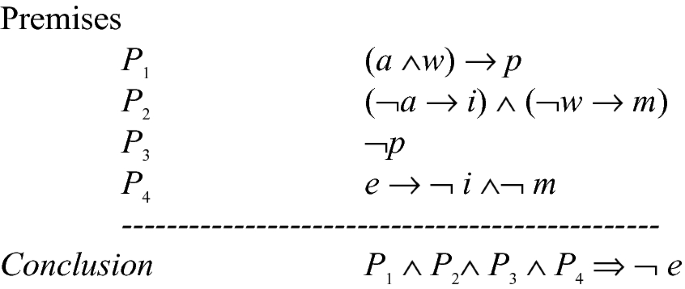
- Mathematicians: From proving theorems to building mathematical structures, propositional calculus is widely used by mathematicians in their daily work.
- Computer Scientists: Propositional calculus forms the basis of several aspects of computer science, including algorithm creation, software programming, and even AI development.
- Logicians: Logic is a key area for philosophers, especially those working on the foundations of mathematics or the philosophy of logic itself, who often dive deep into propositional calculus.
- Cognitive Scientists: Cognitive scientists, psychologists, and even neuroscientists can also use propositional calculus as a model for understanding human thought processes.
- Engineers: Software engineers and developers use propositional calculus when writing code and creating algorithms.
Where is Propositional Calculus Used?
Propositional Calculus is used in myriad applications throughout industry, academia, and technology.
- Mathematics: From set theory to algebra, propositional calculus serves as a useful tool in proving a host of mathematical theorems and statements.
- Computer Science: In CS, some of the fundamental operations such as if-then-else statements, loops, or recursion have their roots in propositional calculus.
- Artificial Intelligence: Within AI, propositional calculus is used when creating algorithms, automating reasoning, and decision-making.
- Programming: Propositional calculus is used extensively on a daily basis by programmers creating and manipulating logic statements and conditionals in numerous programming languages.
- Digital Circuits Design: In electronic engineering, digital circuits are often designed using the principles and concepts of propositional calculus.
When is Propositional Calculus Used?
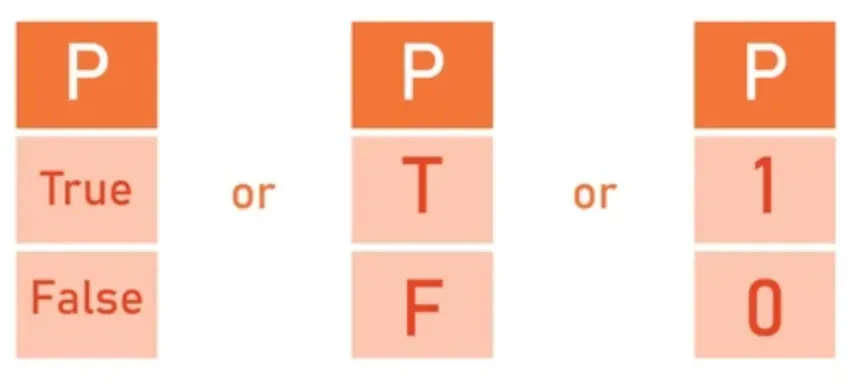
While propositional calculus is ever-present in many professional fields, it's heavily relied on during particular situations and tasks.
- Problem-Solving: Propositional calculus is often used to solve complex problems in mathematics and computer science.
- Algorithm Development: When designing and implementing algorithms, particularly in programming, the use of propositional calculus is almost unavoidable.
- Proving Theorems: In the field of mathematics, proving theorems often involves the intricate use of propositional calculus.
- Digital System Design: Propositional calculus is used for solving problems related to digital system design or logic circuit design.
- Cognitive Modeling: Propositional calculus can aid in creating cognitive models to study and replicate human thinking and decision-making processes.
How to Use Propositional Calculus?
Using propositional calculus requires a solid understanding of its principles and the logic behind its operations.
Understanding Basic Principles
First and foremost, one should grasp the basic ideas and concepts, which include understanding propositions and their truth values.
Familiarity with Connectives
Understanding logical connectives is crucial as they form the core of propositional logic, denoting different types of relationships between propositions.
Learning to Construct Compound Propositions
By combining basic propositions with logical connectives, compound propositions can be constructed – a fundamental skill in propositional calculus.
Understanding Truth Tables
Truth tables, which display possible truth values of a set of propositions, are an integral part of propositional calculus.
Utilizing Laws and Rules of Inference
Once the basics are understood, using different laws of logic and rules of inference, you can manipulate propositions and form logical arguments.
Propositional Calculus: Best Practices
Using propositional calculus effectively requires practice and understanding, and these best practices can help.
- Learning Notation: An integral part of propositional calculus is understanding and correctly utilizing its unique notation.
- Mastering Logical Connectives: A strong command over the five main logical connectives — negation, conjunction, disjunction, implication, and biconditional — is crucial.
- Practicing with Truth Tables: Frequent practice using truth tables can significantly aid in understanding and implementing propositional calculus.
- Applying Laws and Theorems: The application of various laws and theorems within this domain can simplify complex problems.
- Constantly Practicing and Applying: Like any mathematical or logical concept, continual practice and finding practical applications for propositional calculus will enhance anyone's proficiency with it.
Challenges in Understanding Propositional Calculus
While Propositional Calculus is a fascinating and useful domain, it is not without its challenges.
- Understanding Logical Connectives: The various logical connectives used in propositional calculus can initially be quite perplexing and take some time to understand fully.
- Reading and Writing Notation: The unique and abstract notation can also pose challenges when reading or writing statements in propositional calculus.
- Using Truth Tables: Truth tables can become complex when dealing with multiple propositions. As a result, understanding and interpreting them can be a difficult task.
- Applying Laws and Rules: Using and understanding the many laws and rules of inference in propositional calculus is a demanding task and requires deep comprehension.
- Translating Real-World Problems: Applying propositional calculus to real-world problems necessitates the complex task of accurately translating those problems into logical propositions.
Trends in Propositional Calculus
Even this relatively scoped field has seen exciting trends and developments, with many more likely in the future.
- Artificial Intelligence: With the rise of AI and machine learning, the application of propositional calculus in these domains is a trend worth noting.
- Cognitive Science: In cognitive science, propositional calculus is being used to model human thought processes — a recent and exciting development.
- Quantum Computing: In the bleeding-edge field of quantum computing, concepts from propositional calculus are being reinterpreted and applied.
- Computer Science Education: There's a growing trend within computer science education to begin teaching propositional calculus principles at even earlier stages.
- Automation of Logic: Automated reasoning, once a far-fetched dream, is now an active research field. Propositional calculus plays a crucial role in this endeavor.
Frequently Asked Questions (FAQs)
What is the core principle of propositional calculus?
Propositional calculus, in logic, deals with propositions and their relationship with logical connectives. It's about determining the validity of compound statements based on the truth values of their components.
How does propositional calculus differ from predicate calculus?
Unlike propositional calculus which treats propositions as atomic units, predicate calculus breaks down propositions into predicates, quantifiers, and variables, providing a more granular analysis.
What are the main operators in propositional calculus?
The main operators are 'not' (negation), 'and' (conjunction), 'or' (disjunction), 'implies' (implication), and 'if and only if' (biconditional).
What role does propositional calculus play in computer science?
Propositional calculus is foundational to areas like boolean algebra, digital circuit design, programming logic, and artificial intelligence, making it vital in computer science.
Can propositional calculus handle ambiguity?
Propositional calculus only deals with clear-cut true or false propositions. For uncertain or ambiguous conditions, fuzzy logic, a more advanced branch of logic, is used.