What is Logical Deduction?
Logical deduction is the process of drawing conclusions based on premises or statements that are known or assumed to be true. It involves using reasoning and logical principles to derive new information or insights.
The main purpose of logical deduction is to make valid and sound arguments and arrive at accurate conclusions. It helps us analyze and evaluate information, solve problems, and make informed decisions.
How does Logical Deduction Work?
Logical deduction operates on the principles of deductive logic. It starts with a set of premises or statements and applies logical rules to derive a conclusion.
This process ensures that the conclusion is necessarily true if the premises are true. Here’s a more detailed explanation.

Establishing Premises
Logical deduction starts by laying down one or more assumptions or premises. These must be regarded as mutual truths for the duration of the deduction process.
Applying Deductive Reasoning
Deductive reasoning is applied to the premises. This involves a systematic approach, in essence saying, "If A and B are true, then C must also be true."
Leading to a Necessary Conclusion
From the given premises and using the principles of logic, logical deduction leads to a necessary conclusion. If the premises are true and the reasoning process is correct, this conclusion is irrefutably true.
Assurance of Truth Preservation
A crucial aspect of logical deduction is that it's truth-preserving. This means if the original statements (premises) are true, then the derived statement (conclusion) is also guaranteed to be true.
Checks And Balances
The process is rechecked to ensure no leaps of logic have been made. This acts as a confirmation of the conclusion's validity, reinforcing the confidence in the result of the logical deduction.
The Four-Fold Classification of Propositions
Logical deduction involves working with different types of propositions. These propositions can be classified into four categories:
- Universal Affirmative Proposition (A): These propositions affirm that all members of a particular group have a certain property.
- Universal Negative Proposition (E): These propositions state that no member of a particular group has a certain property.
- Particular Affirmative Proposition (I): These propositions affirm that some members of a particular group have a certain property.
- Particular Negative Proposition (O): These propositions state that some members of a particular group do not have a certain property.
Steps in Applying Logical Deduction
To solve logical deductions, we need to understand categorical statements or propositions. These statements can be expressed in a standard form, consisting of a quantifier, subject term, copula, and predicate term.
In order to apply logical deduction successfully, we need to follow these steps:
Step 1:Identify the Premises
The first step towards applying logical deduction is to identify the premises or assumptions. These are the statements or facts that you already know or consider to be true.
Step 2:Formulate a Hypothesis
Next, you need to formulate a hypothesis. This is an initial assumption you make based on the premises, which leads you towards a conclusion.
Step 3:Apply Laws of Logic
Now, you apply the laws of logic to your premises and hypothesis. These laws (like Law of Identity, Law of Non-Contradiction, and Law of Excluded Middle) provide a framework for logical reasoning and deduction.
Step 4:Draw a Conclusion
Following the laws of logic, you deduce a conclusion. If the premises and hypothesis are true, then this conclusion derived logically from them should also be true.
Step 5:Evaluate and Reflect
After deducing a conclusion, it is critical to evaluate your result and reflect on the whole logical deduction process. Verify the conclusion with real-life scenarios or additional data, if possible.
Differences between Logical Deduction and Syllogism
The main difference is all syllogisms are logical deductions, but not all logical deductions are syllogisms. Like how all dogs are animals, but not all animals are dogs. Here’s how:
Logical Deduction
This is a method of reasoning where you conclude something based on what's known or assumed to be true.
If you love peanut butter and all sandwiches with peanut butter are delicious, logically deducted, you'd find any peanut butter sandwich tasty!
Syllogism
Syllogism is a type of logical deduction. It's a little more structured. It involves two statements made (referred to as premises), followed by a conclusion.
For instance, premise 1: all men are mortal. Premise 2: John is a man. Conclusion: John is mortal. Neat, right?
Suggested Reading:Argumentation Framework
Types of Logical Reasoning
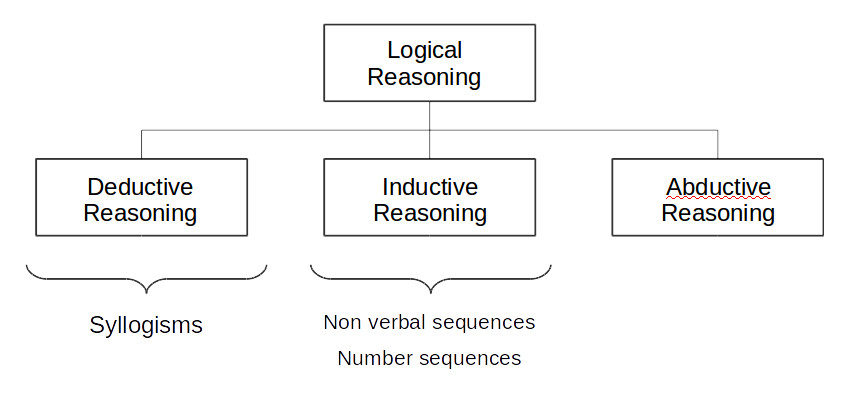
Logical deduction is part of a broader framework of logical reasoning. Here are the main types of logical reasoning:
Deductive Reasoning
Deductive reasoning involves drawing a specific logical conclusion from a general statement or set of statements.
It follows a top-down approach, starting with general principles and arriving at a specific conclusion.
Inductive Reasoning
Inductive reasoning involves making broad generalizations or predictions based on specific observations or evidence.
It follows a bottom-up approach, starting with specific instances and arriving at a general conclusion.
Abductive Reasoning
Abductive reasoning is about making educated guesses or plausible explanations based on limited information.
It involves inferring the best explanation for a given set of observations or facts.
Applications of Logical Deduction
In this section, we'll explore some of the key applications of logical deduction, showing how this type of reasoned thinking isn't just for the likes of Sherlock Holmes, but plays a pivotal role across multiple disciplines and industries.
Mathematics and Logic
Logical deduction is the heart and soul of mathematics and logic studies. It assists in understanding and proving mathematical theorems and equations.
Problem-Solving and Decision Making
Logical deduction aids in comprehending problems, formulating solutions, and making decision-making more evidence-based and rational.
It's a critical tool in disciplines ranging from business management to scientific research.
Computer Programming
In computer science, logical deduction proves vital for programming tasks, algorithm development, and debugging.
Logical reasoning helps programmers anticipate the outcomes of different code paths and resolve software issues efficiently.
Law and Judiciary
In legal studies and judicial proceedings, logical deduction is often used to evaluate evidence, form arguments, and arrive at verdicts.
Both lawyers and judges use it in their reasoning and decision making.
Artificial Intelligence
In AI, logical deduction plays a crucial role in developing intelligent systems capable of solving complex problems, like in game-playing (chess algorithms) or knowledge representation (rules in expert systems).
Understanding and mastering the art of logical deduction can help improve our reasoning skills, and it has vast applications in numerous professional and academic fields.
Frequently Asked Questions (FAQs)
What is logical deduction?
Logical deduction is a process of reasoning in which a logical conclusion is drawn from given premises using deductive logic.
How does logical deduction relate to problem-solving?
Logical deduction is an essential tool in problem-solving. It helps break complex problems down into smaller parts, determine the key factors involved, and arrive at a logical solution.
What is the difference between deductive reasoning and inductive reasoning?
Deductive reasoning involves drawing specific logical conclusions from a more general set of premises or assumptions that are known to be true, whereas inductive reasoning uses specific observations to make broader generalizations or predictions.
What are the steps involved in applying logical deduction?
The three key steps for logical deduction are to identify the premises in a given statement, make connections between the premises, and test the conclusion reached using deductive logic.
What are some practical applications of logical deduction?
Logical deduction is used in various fields, including scientific research, problem-solving, critical thinking, and argumentation.
It enhances analytical skills, enables informed decision-making, and reinforces the power to recognize biases and fallacies.

